Bộ 5 đề thi cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 05
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho \(b\) là một phần tử của tập hợp \(S\). Mệnh đề nào dưới đây đúng?
\(b \subset S\).
\(b \in S\).
\(S \subset b\).
\(\left\{ b \right\} \in S\).
Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\},B = \left\{ {2;3;5;6;7} \right\}\). Khi đó \(A \cap B = ?\)
\(\left\{ {2;3} \right\}\).
\(\left\{ 3 \right\}\).
\(\left\{ {3;5} \right\}\).
\(\left\{ {2;3;5} \right\}\).
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất 2 ẩn \(x,y\)?
\(\left\{ \begin{array}{l}xy - y < - 3\\x + 2y \ge - 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - y < - 3\\x + {5^2}y \ge - 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - y < - 3\\{x^2} + 2xy \ge - 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - {y^2} < - 3\\x + y \ge - 4\end{array} \right.\).
Biết miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y \ge m\\x - 5y < m + 2\end{array} \right.\) chứa gốc tọa độ \(O\left( {0;0} \right)\). Có bao nhiêu giá trị nguyên của tham số \(m\) thỏa mãn hệ bất phương trình trên?
1.
4.
3.
2.
Gọi \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\) của hình bình hành \(ABCD\). Đẳng thức nào sau đây là đẳng thức sai?
\(\overrightarrow {OA} = \overrightarrow {OC} \).
\(\overrightarrow {AB} = \overrightarrow {DC} \).
\(\overrightarrow {CB} = \overrightarrow {DA} \).
\(\overrightarrow {OB} = \overrightarrow {DO} \).
Cho tam giác \(ABC\), gọi \(M\) là trung điểm của \(BC\) và \(G\) là trọng tâm của tam giác \(ABC\). Mệnh đề nào sau đây đúng?
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AM} \).
\(\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
\(\overrightarrow {AG} = \frac{3}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
\(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AM} \).
Cho hình vuông \[ABCD\] có cạnh bằng \[a\]. Độ dài \[\left| {\overrightarrow {AD} + \overrightarrow {AB} } \right|\] bằng
\(2a\).
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{{a\sqrt 3 }}{2}\).
\(a\sqrt 2 \).
Cho tam giác ABC có \(AB = 5;AC = 8;BC = 7\)thì \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng:
-20.
40.
10.
20.
Làm tròn số của \(2,57656\) đến hàng phần chục ta được kết quả là
\(2,57\).
\(2,58\).
\(2,5\).
\(2,6\).
Cho số gần đúng \(a = 869265\) với độ chính xác \(d = 50\). Số quy tròn của số \(a\) là
\(869300\).
\(869270\).
\(869200\).
\(869260\).
Trung vị của mẫu số liệu là
\(7\).
\(6\).
\(7,5\).
\(1,5\).
Khoảng tứ phân vị của mẫu số liệu là
\(7\).
\(6\).
\(7,5\).
\(1,5\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ \(A\) thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ \(B\) thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20 . Gọi \(x,y\) theo thứ tự là số lần người chơi chọn được chữ \(A\) và chữ \(B\). Khi đó:
Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
Bất phương trình bậc nhất hai ẩn \(x,y\) trong tình huống người chơi chiến thắng là \(3x - y \ge 18.\)
Người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 4 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Các mệnh đề sau đúng hay sai?
Parabol \(y = - 2{x^2} + 4x - 7\) có trục đối xứng là \(x = 1\).
Paraol \(y = 3{x^2} + 5x + 2\) có tọa độ đỉnh \(I\left( { - \frac{5}{6}; - \frac{1}{{12}}} \right)\).
Parabol \(y = {x^2} + 5x - 6\) cắt trục hoành tại \(A\left( {1;0} \right)\) và \(B\left( { - 6;0} \right)\).
Parabol \(y = 3{x^2} + 6x - 1\) đồng biến trên \(\left( { - 2017; - 1} \right)\).
Cho \(\sin \alpha = \frac{2}{3}\left( {90^\circ < \alpha < 180^\circ } \right)\,\)
\(\cos \alpha < 0\).
\(\cos \alpha = - \frac{{\sqrt 5 }}{3}\).
\(\frac{{\sin \alpha + 2\sqrt 5 \cos \alpha }}{{2\sin \alpha + \sqrt 5 \cos \alpha }} = \frac{4}{3}\).
\(\frac{{\sin \alpha - \cos (180^\circ - \alpha )}}{{\sin \left( {90^\circ - \alpha } \right) + \sin (180^\circ - \alpha )}} = - 1\).
Cho tam giác \(ABC\) có có \(AB = 4\sqrt 2 ,AC = 6,\widehat {BAC} = 45^\circ \). Gọi \(D\) là trung điểm của đoạn thẳng \(BC\). Điểm \(E\) thoả mãn \(\overrightarrow {AE} = k\overrightarrow {AC} (k \in \mathbb{R})\) (tham khảo hình vẽ). Khi đó: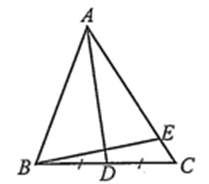
\(\overrightarrow {AB} \cdot \overrightarrow {AC} = 20\).
\(\overrightarrow {AD} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \).
\(BC = 3\sqrt 5 \).
\(AD \bot BE\) khi \(k = \frac{{14}}{{15}}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Anh T cần đặt một tiệc cưới ước tính khoảng 30 đến 35 bàn.
Nhà hàng 1: đề nghị anh T đóng tiền cố định 20 triệu đồng, sau khi tiệc cưới diễn ra thì sẽ đóng khoản còn lại với số tiền 2 triệu đồng/1 bàn.
Nhà hàng 2: đề nghị anh T đóng tiền cố định 10 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn lại với số tiền 2,5 triệu/1 bàn.
Để tiết kiệm được chi phí cho tiệc cưới, anh T nên lựa chọn nhà hàng \(n\) (giả sử chất lượng phục vụ hai nhà hàng trên là ngang nhau). Giá trị \(n\) bằng bao nhiêu?
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là \(27\) (triệu đồng) và bán ra với giá là \(31\) triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là \(600\) chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm \(1\) triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm \(200\) chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu triệu đồng để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất?
Cho tam giác \(ABC\) có \(AB = 4\;{\rm{cm}},\,\,\widehat A = 40^\circ ,\,\,\widehat C = 60^\circ \). Diện tích tam giác \(ABC\) bằng bao nhiêu \({\rm{c}}{{\rm{m}}^{\rm{2}}}\)?( làm tròn đến hàng phần trăm).
Để đo chiều cao của một cột cờ trên đỉnh một toà nhà anh Bắc đã làm như sau: Anh đứng trên một đài quan sát có tầm quan sát cao 5 m so với mặt đất, khi quan sát anh đo được góc quan sát chân cột là \(40^\circ \) và góc quan sát đỉnh cột là \(50^\circ \), khoảng cách từ vị trí quan sát đến tòa nhà là \(18{\rm{m}}\). Tổng chiều cao cột cờ và chiều cao của toà nhà là bao nhiêu mét? (Làm tròn đến hàng phần mười).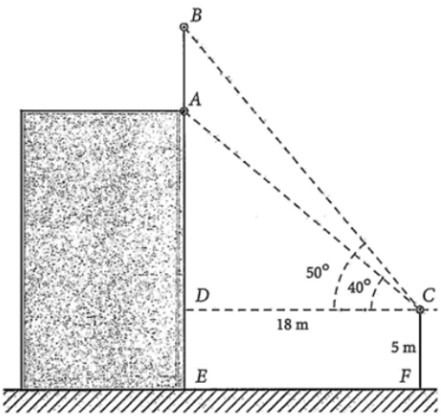
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động vào một vật đặt tại điểm \(O\). Biết hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều có cường độ là 20 N và chúng hợp với nhau một góc \(80^\circ \). Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu Newton (kết quả làm tròn đến hàng phần trăm)?
Hai đảo \(A\) và \(B\) cách bờ một khoảng \(AD = 30\)km và \(BC = 20\) km (như hình vẽ). Người ta muốn dựng một trạm phát sóng\(M\) trên bờ \(DC\) sao cho khoảng cách từ trạm phát sóng đến hai đảo bằng nhau. Biết khoảng cách giữa hai vị trí \(D\) và \(C\) bằng \(50\) km. Tính khoảng cách từ trạm phát sóng đến hai đảo (đơn vị km) (kết quả làm tròn đến hàng phần trăm).