Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 2
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Trong các câu sau, câu nào không phải là mệnh đề ?
Mặt Trời xoay quanh Trái Đất;
Với \(x = 2\) thì \[x - 2 < 5\];
Trái Đất xoay quanh Mặt Trời;
\(x > 6\).
Biểu diễn mệnh đề “Tồn tại số thực \(x\) để \(x\) chia hết cho 2” dưới dạng kí hiệu là
“\(\forall x \in \mathbb{Z}|x\,\, \vdots \,\,2\)”;
“\(\forall x \in \mathbb{R}|x\,\, \vdots \,\,2\)”;
“\(\exists x \in \mathbb{Z}|x\,\, \vdots \,\,2\)”;
“\(\exists x \in \mathbb{R}|x\,\, \vdots \,\,2\)”.
Mệnh đề phủ định của mệnh đề “\(\forall x \in \mathbb{N}|x \ge 0\)” là mệnh đề
“\(\forall x \in \mathbb{N}|x > 0\)”;
“\(\forall x \in \mathbb{N}|x < 0\)”;
“\(\exists x \in \mathbb{N}|x \ge 0\)”;
“\(\exists x \in \mathbb{N}|x < 0\)”.
Tính chất đặc trưng của các phần tử thuộc tập hợp \(L = \left\{ {x \in \mathbb{N}|x \le 10} \right\}\)
Đều là các số nguyên nhỏ hơn hoặc bằng 10;
Đều là các số tự nhiên nhỏ hơn 10;
Đều là các số tự nhiên nhỏ hơn hoặc bằng 10;
Đều là các số thực nhỏ hơn hoặc bằng 10.
Cho hai tập hợp: \(A = \left\{ {2;\,\,4;\,\,6;\,\,8;\,\,10} \right\}\) và \(B = \left\{ {x\,\, \vdots \,\,2|x \in \mathbb{N},x < 20} \right\}\). Khẳng định nào sau đây là đúng ?
\(A \subset B\);
\(B \subset A\);
\(A = B\);
\(x \in B \Rightarrow x \in A\).
Khẳng định nào sau đây là sai ?
\(\mathbb{N} = {\mathbb{N}^*}\);
\({\mathbb{N}^*} \subset \mathbb{N}\);
\(\mathbb{Z} \subset \mathbb{R}\);
\(\mathbb{N} \subset \mathbb{Q}\).
Phân số \(\frac{1}{4}\) thuộc tập hợp nào sau đây ?
\(\mathbb{N}\);
\({\mathbb{N}^*}\);
\(\mathbb{Z}\);
\(\mathbb{Q}\).
Cho hai tập hợp: \(M = \left\{ {x \ge 0|{x^2} < 4} \right\}\) và \(N = \left\{ {x \in \mathbb{R}| - 4 < x - 5 < 4} \right\}\). Biết \(L = M \cap N\). Vậy ta có: \(L = ?\)
\(\left[ {1;\,\,2} \right]\);
\(\left( {1;\,\,2} \right)\);
\(\left[ {0;\,\,4} \right]\);
\(\left( {0;\,\,4} \right)\).
Bất phương trình nào dưới đây là bất phương trình bậc nhất hai ẩn ?
\(x - {y^2} \ge 2\);
\({x^3} + 7y < 0\);
\(4x - 9y > - 3\);
\(x - y + z < 1\).
Một nghiệm của bất phương trình bậc nhất hai ẩn \(3x - 5y \ge 2\) là
\(\left( {3;\,\,2} \right)\);
\(\left( {3;\,\,1} \right)\);
\(\left( { - 3;\,\,1} \right)\);
\(\left( {3;\,\,5} \right)\).
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(x - y < 1\) là
Nửa mặt phẳng (không kể bờ) có bờ là đường thẳng \(x - y = 0\) và chứa điểm \(O\left( {0;\,\,0} \right)\);
Nửa mặt phẳng (có kể bờ) có bờ là đường thẳng \(x - y = 0\) và chứa điểm \(O\left( {0;\,\,0} \right)\);
Nửa mặt phẳng (có kể bờ) có bờ là đường thẳng \(x - y = 1\) và chứa điểm \(O\left( {0;\,\,0} \right)\);
Nửa mặt phẳng (không kể bờ) có bờ là đường thẳng \(x - y = 1\) và chứa điểm \(O\left( {0;\,\,0} \right)\).
Trong các hệ bất phương trình sau, đâu không phải là hệ bất phương trình bậc nhất hai ẩn ?
\(\left\{ \begin{array}{l}x - y > 4\\2x + y < 19\end{array} \right.\);
\(\left\{ \begin{array}{l}x - 2y \le 0\\2x + y < 19\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^2} - y > 0\\x + y < 6\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y - 3 > 4\\2x + y + 2 < 19\end{array} \right.\).
Phần tô đậm nào của hình ảnh sau đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}x - 2y \le 0\\2x + 3y < 10\end{array} \right.\) ?
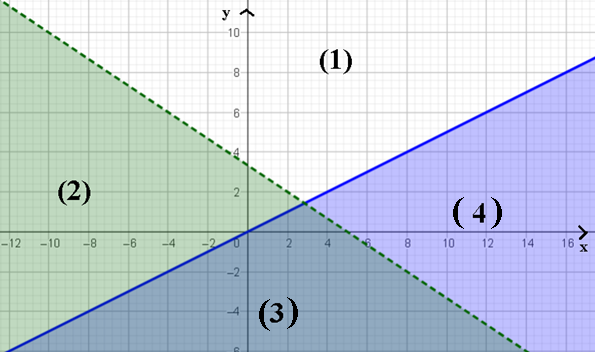
(1);
(2);
(3);
(4).
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 180^\circ \), \(\sin \alpha \) có thể nhận giá trị nào sau đây ?
\(\frac{1}{3}\);
\(\frac{4}{3}\);
\(\frac{{ - 7}}{5}\);
\(\frac{{ - 3}}{2}\).
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 180^\circ \). Khi đó, \[\cos \alpha = ?\]
\[\cos \left( {\alpha + 90^\circ } \right)\];
\[ - \cos \left( {180^\circ - \alpha } \right)\];
\[ - \cos \alpha \];
\[1 - \cos \left( \alpha \right)\].
Cho góc \(\alpha \) biết \(0^\circ \le \alpha \le 180^\circ \), biết \[\cos \alpha = \frac{1}{4}\]. Khi đó giá trị của \(\tan \alpha \) bằng
\(\frac{1}{{\sqrt {15} }}\);
\[\sqrt {15} \];
\(\frac{1}{4}\);
\(\frac{{\sqrt {15} }}{4}\).
Cho tam giác có độ dài ba cạnh lần lượt là \(a\), \(b\), \(c\), các góc đối diện các cạnh đó lần lượt là \(\alpha \), \(\beta \), \(\varphi \), diện tích tam giác đó là \(S\), nửa chu vi tam giác là \(p\). Khẳng định nào sau đây là sai ?
\(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \varphi }}\);
\({a^2} = {b^2} + {c^2} - 2bc \cdot \cos \alpha \);
\({a^2} + {c^2} = {b^2} + 2ac \cdot \cos \beta \);
\({a^2} = {b^2} - {c^2} + 2bc \cdot \cos \alpha \).
Cho tam giác có độ dài ba cạnh lần lượt là \(a\), \(b\), \(c\), các góc đối diện các cạnh đó lần lượt là \(\alpha \), \(\beta \), \(\varphi \), các đường cao tương ứng lần lượt là \({h_a}\), \({h_b}\), \({h_c}\), diện tích tam giác đó là \(S\), nửa chu vi tam giác là \(p\). Khẳng định nào sau đây là sai ?
\(S = \frac{1}{2}a{h_a}\);
\(S = \frac{1}{2}bc\sin \alpha \);
\(S = \frac{1}{2}ab\sin \varphi \);
\(S = \sqrt {p\left( {p + a} \right)\left( {p + b} \right)\left( {p + c} \right)} \).
Cho tam giác \(ABC\) có \(AB = 5\,\,cm\), \(AC = 7\,cm\), \(BC = 6\,\,cm\). Số đo \(\widehat {ABC}\) là (làm tròn kết quả đến độ)
\(79^\circ \);
\(78^\circ \);
\(77^\circ \);
\(76^\circ \).
Cho tam giác \(ABC\) có \(AC = 11\,\,\,cm\), \(BC = 9\,\,cm\), \(\widehat {ACB} = 58^\circ \). Độ dài cạnh \(AB\) là (làm tròn kết quả đến hàng đơn vị)
10 cm;
9 cm;
8 cm;
7 cm.
Ta không thể vận dụng định lí sin, định lí côsin để giải một tam giác thường nếu biết những yếu tố nào sau đây ?
Số đo một góc và độ dài hai cạnh;
Độ dài ba cạnh;
Số đo hai góc và độ dài một cạnh;
Độ dài hai cạnh.
Cho tam giác \(MNP\) có \(MN = 4\,cm\), \(\widehat {MNP} = 30^\circ \), \(\widehat {MPN} = 45^\circ \). Độ dài cạnh \(MP\) là
2 cm;
3 cm;
\(2\sqrt 2 \) cm;
\(3\sqrt 2 \) cm.
Cho đoạn thẳng \(AB\) có trung điểm \(M\). Khẳng định nào sau đây là đúng ?
Giá của vectơ \(\overrightarrow {AM} \) là đường trung trực của đoạn thẳng \(AB\);
Điểm đầu của vectơ \(\overrightarrow {AM} \) là \(M\);
Điểm cuối của vectơ \(\overrightarrow {BA} \) là \(B\);
Giá của vectơ \(\overrightarrow {MB} \) là đường thẳng \(AB\).
Cho hình vuông \(ABCD\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng;
\(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) ngược hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không cùng phương.
Cho ba điểm \(A\), \(B\), \(C\) phân biệt. Ta có: \(\overrightarrow {AC} = ?\)
\(\overrightarrow {AB} - \overrightarrow {BC} \);
\(\overrightarrow {BC} - \overrightarrow {BA} \);
\(\overrightarrow {BC} - \overrightarrow {AB} \);
\(\overrightarrow {AB} + \overrightarrow {CB} \).
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} = \overrightarrow {CD} \);
\(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {CB} \);
\(\overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \);
\(\overrightarrow {AD} - \overrightarrow {AB} = \overrightarrow {AC} \).
Cho tam giác \(ABC\) đều có chu vi là 18 cm. Độ dài vectơ \(\overrightarrow v = \overrightarrow {AB} - \overrightarrow {AC} \) là
8 cm;
7 cm;
6 cm;
0 cm.
Cho ba điểm phân biệt \(M\), \(N\), \(P\), biết \(\overrightarrow {MN} = \overrightarrow {NP} \). Khẳng định nào sau đây là đúng ?
\(M\) là trung điểm của đoạn thẳng \(NP\);
\(N\) nằm ngoài đoạn thẳng \(MP\);
\(N\) là trung điểm của đoạn thẳng \(MP\);
\(M\), \(N\), \(P\) không thẳng hàng.
“Tích của một vectơ với một số là …..”. Điền từ thích hợp vào chỗ trống.
Một vectơ;
Một đoạn thẳng;
Một số;
Một hình tam giác.
Cho đoạn thẳng \(AB\) có trung điểm \(M\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow {AB} = \overrightarrow {AM} \);
\(\overrightarrow {AB} = \frac{1}{2}\overrightarrow {AM} \);
\(\overrightarrow {AB} = 2\overrightarrow {AM} \);
\(\overrightarrow {AB} = - 2\overrightarrow {AM} \).
Cho hình thoi \(ABCD\) tâm \(O\) như hình vẽ dưới, khi đó ta có: \(\overrightarrow {AO} = .....\overrightarrow {CM} \). Điền số thích hợp vào chỗ trống.
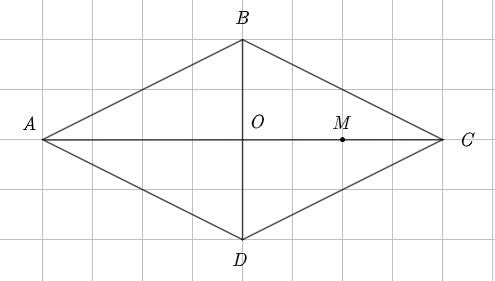
– 1;
– 2;
1;
2.
Cho tam giác \(MOP\) và hai điểm \(A\), \(B\) lần lượt nằm trên hai cạnh \(MO\) và \(OP\) sao cho \(MA = \frac{1}{5}MO\) và \(OB = \frac{3}{4}OP\). Phân tích vectơ \(\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {MA} \) và \(\overrightarrow {OB} \) ta được
\(\overrightarrow {MP} = 5\overrightarrow {MA} + \frac{4}{3}\overrightarrow {OB} \);
\(\overrightarrow {MP} = 5\overrightarrow {MA} + \frac{3}{4}\overrightarrow {OB} \);
\(\overrightarrow {MP} = 5\overrightarrow {MA} - \frac{4}{3}\overrightarrow {OB} \);
\(\overrightarrow {MP} = \frac{1}{5}\overrightarrow {MA} + \frac{3}{4}\overrightarrow {OB} \).
Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác vectơ – không, ta có: \(\overrightarrow u \cdot \overrightarrow v = ?\)
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right|\);
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| + \left| {\overrightarrow v } \right|\);
\(\overrightarrow u \cdot \overrightarrow v = \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\);
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
Cho tam giác đều \(ABC\) cạnh bằng 4. Tích vô hướng \[\overrightarrow {AB} \cdot \overrightarrow {AC} \] bằng
7;
8;
9;
10.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) biết \(\left| {\overrightarrow a } \right| = 4\), \(\left| {\overrightarrow b } \right| = 5\) và \(\overrightarrow a \cdot \overrightarrow b = 4\). Số đo của góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là (làm tròn kết quả đến độ)
\(77^\circ \);
\(78^\circ \);
\(79^\circ \);
\(80^\circ \).
II. Tự luận (3 điểm)
(1 điểm) Cửa hàng của cô Liên có hai loại bưởi, bưởi loại I có giá là 400 000 đồng một quả, bưởi loại II có giá là 80 000 đồng một quả. Cô Liên chọn một lượng bưởi để làm giỏ quà cho khách hàng, biết số bưởi loại II ít nhất phải chọn là 5 quả. Do điều kiện kinh tế của khách nên số bưởi loại I phải chọn tối đa là 4 quả. Biết chọn 1 quả bưởi loại I có lãi 10 000 đồng, chọn 1 quả bưởi loại II có lãi 2 000 đồng. Khách hàng chỉ chi tối đa 1 600 000 đồng cho giỏ quà. Cô Liên cần chọn bưởi như thế nào để thu được lãi cao nhất ?
(1 điểm) Bạn Nam đứng ở chân một tòa nhà, Nam nhìn hướng lên \(24^\circ \) thì thấy ngọn của một cái cây. Và nếu Nam đứng ở đỉnh của tòa nhà ấy, biết tòa nhà cao 155 m, Nam nhìn hướng xuống một góc \(60^\circ \) so với phương nằm ngang để thấy ngọn của cái cây đó. Tính chiều cao của cái cây (làm tròn đến hàng phần trăm).
(1 điểm) Cho tam giác \(ABC\) đều cạnh \(a\) có trọng tâm \(G\), điểm \(M\) là điểm bất kì thuộc đường tròn tâm \(G\) có bán kính bằng \(\frac{{a\sqrt 2 }}{3}\). Chứng minh rằng:
\(\overrightarrow {MA} \cdot \overrightarrow {MB} + \overrightarrow {MB} \cdot \overrightarrow {MC} + \overrightarrow {MC} \cdot \overrightarrow {MA} = \frac{{{a^2}}}{6}\).