Bộ 5 đề thi giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 05
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mệnh đề phủ định của mệnh đề “2018 là số tự nhiên chẵn” là
2018 là số chẵn.
2018 là số nguyên tố.
2018 không là số tự nhiên chẵn.
2018 là số chính phương.
Cho \(x\) là một phần tử của tập hợp \(X\). Mệnh đề nào sau đây là đúng?
\(x \in X\).
\(X \in x\).
\(x \subset X\).
\(\left\{ x \right\} \in X\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}|2 \le x < 5} \right\}\). Phần bù của tập hợp \(A\) trong \(\mathbb{R}\) là tập nào sau đây?
\(\left[ {5; + \infty } \right)\).
\(\left( { - \infty ;2} \right)\).
\(\left( { - \infty ;2} \right] \cup \left( {5; + \infty } \right)\).
\(\left( { - \infty ;2} \right) \cup \left[ {5; + \infty } \right)\).
Trong các mệnh đề sau, mệnh đề nào đúng?
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm có tọa độ là nghiệm của bất phương trình \(ax + by \le c\) (các hệ số \(a,b,c\) là những số thực, \(a\) và \(b\) không đồng thời bằng 0) không được gọi là miền nghiệm của nó.
Biểu diễn tập nghiệm của bất phương trình \(2x - 3y + 1 < 0\) trên hệ trục \(Oxy\) là đường thẳng \(2x - 3y + 1 = 0\).
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm có tọa độ là nghiệm của bất phương trình \(ax + by \le c\) (các hệ số \(a,b,c\) là những số thực, \(a\) và \(b\) không đồng thời bằng 0) được gọi là miền nghiệm của nó.
Nghiệm của bất phương trình \(ax + by \le c\) (các hệ số \(a,b,c\) là những số thực, \(a,b\) không đồng thời bằng 0) là tập rỗng.
Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y - 2 \le 0\\2x - 3y + 2 > 0\end{array} \right..\)
\(\left( {0;0} \right)\).
\(\left( {1;1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( { - 1; - 1} \right)\).
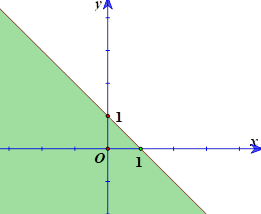
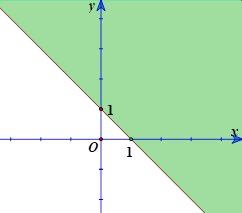
Miền nghiệm của bất phương trình \(x + y \le 1\) (phần không tô mầu) là
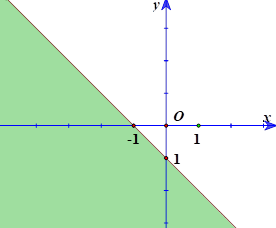
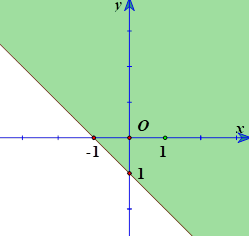
Cho góc \(\alpha \in \left( {90^\circ ;180^\circ } \right)\). Khẳng định nào sau đây đúng?
\(\sin \alpha \) và \(\cot \alpha \) cùng dấu.
Tích \(\sin \alpha .\cot \alpha \) mang dấu âm.
Tích \(\sin \alpha .\cos \alpha \) mang dấu dương.
\(\sin \alpha \) và \(\tan \alpha \) cùng dấu.
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
\(S = \frac{{abc}}{{4r}}\).
\(r = \frac{{2S}}{{a + b + c}}\).
\({a^2} = {b^2} + {c^2} + 2bc\cos A\).
\(S = r\left( {a + b + c} \right)\).
Biết \(\cos \alpha = \frac{2}{3}\left( {0^\circ < \alpha < 90^\circ } \right)\). Khi đó \(\tan \alpha \) bằng
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{\sqrt 5 }}{2}\).
\(\frac{2}{{\sqrt 5 }}\).
\( - \frac{2}{{\sqrt 5 }}\).
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\) của hình bình hành \(ABCD\). Đẳng thức nào sau đây là đẳng thức sai?
\(\overrightarrow {OB} = \overrightarrow {DO} \).
\(\overrightarrow {AB} = \overrightarrow {DC} \).
\(\overrightarrow {OA} = \overrightarrow {OC} \).
\(\overrightarrow {CB} = \overrightarrow {DA} \).
Gọi \(G\) là trọng tâm của tam giác \(ABC\) và \(M\) là điểm bất kì. Chọn khẳng định sai trong các khẳng định sau?
\(\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 \).
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MG} \).
Cho tam giác \(ABC\), \(E\) là điểm trên đoạn BC sao cho \(BE = \frac{1}{4}BC\). Tìm khẳng định đúng?
\(\overrightarrow {AE} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \).
\(\overrightarrow {AE} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \).
\(\overrightarrow {AE} = 3\overrightarrow {AB} + 4\overrightarrow {AC} \).
\(\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{5}\overrightarrow {AC} \).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho các tập hợp\(A = \left\{ {x \in \mathbb{N}|0 \le x \le 4} \right\}\); \(B = \left\{ {0;1;2} \right\}\); \(C = \left\{ { - 3;0;1;2} \right\}\). Các câu sau đúng hay sai?
a) \(B \subset A\).
b) \(\left( {A \cap C} \right)\backslash B = \emptyset \).
c) \(A \cup \left( {C\backslash B} \right) = \left\{ { - 3;0;1;4} \right\}\).
d) \({C_A}B = \left\{ {1;3;4} \right\}\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y \le 240\\y \ge 40\\x \ge 3y\end{array} \right.\). Các câu sau đúng hay sai?
a) Hệ trên là hệ bất phương trình bậc nhất hai ẩn.
b) Điểm \(C\left( {200;40} \right)\) không thuộc miền nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ bất phương trình là một tứ giác.
d) \(x = 120;y = 40\) là nghiệm của hệ bất phương trình để biểu thức \(F = 3x - y\) đạt giá trị nhỏ nhất.
Cho tam giác \(ABC\), biết \(b = 7,c = 5,\cos A = \frac{3}{5}\). Các câu sau đúng hay sai.
a) \(S = 2pr\).
b) \(S = 14\).
c) \(a = 3\sqrt 2 \).
d) \(r = 4 - \sqrt 2 \).
Cho tam giác \(ABC\) có \(AB = 2,AC = 3,\widehat {BAC} = 60^\circ \). Gọi \(M\) là trung điểm của đoạn thẳng \(BC\). Điểm D thỏa mãn \(\overrightarrow {AD} = \frac{7}{{12}}\overrightarrow {AC} \). Các mệnh đề sau đúng hay sai?
a) \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
b) \(\overrightarrow {BD} = 7\overrightarrow {AC} - 12\overrightarrow {AB} \).
c) \(\overrightarrow {AB} .\overrightarrow {AC} = 3\sqrt 3 \).
d) \(AM \bot BD\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Cho hai tập \(A = \left( { - \infty ;m} \right)\) và \(B = \left[ {2m - 2;2m + 2} \right]\). Tìm giá trị nguyên của \(m\) nhỏ hơn 6 để \(\left( {{C_\mathbb{R}}A} \right) \cap B \ne \emptyset \).
Nhu cầu canxi tối thiếu cho một người đang ở độ tuổi trưởng thành trong một ngày là 1300 mg. Trong một lạng đậu nành có 165 mg canxi, một lạng thịt có 15 mg canxi. Gọi \(x;y\) lần lượt là số lạng đậu nành và số lạng thịt mà một người đang ở độ tuổi trưởng thành ăn trong một ngày. Bất phương trình bậc nhất hai ẩn \(x;y\) để biểu diễn lượng canxi cần thiết trong một ngày của một người đang trong độ tuổi trưởng thành có dạng \(bx + 15y \ge a\) với \(a;b\) là các số nguyên dương. Tính giá trị \(T = \frac{a}{2} - 3b\).
Nhân dịp tết Trung thu, xí nghiệp sản xuất bánh muốn sản xuất hai loại bánh: bánh nướng và bánh dẻo. Để sản xuất hai loại bánh này, xí nghiệp cần: đường, bột mì, trứng, mứt bí, lạp xưởng. Xí nghiệp đã nhập về 600 kg bột mì và 240 kg đường, các nguyên liệu khác luôn đáp ứng được số lượng mà xí nghiệp cần. Mỗi chiếc bánh nướng cần 120 g bột mì, 60 g đường. Mỗi chiếc bánh dẻo cần 160 g bột mì và 40 g đường. Theo khảo sát thị trường sản phẩm của xí nghiệp sản xuất luôn được tiêu thụ hết. Mỗi chiếc bánh nướng lãi 8000 đồng, mỗi chiếc bánh dẻo lãi 6000 đồng. Để đáp ứng nhu cầu thị trường; đảm bảo lượng bột mì, đường không vượt quá số lượng mà xí nghiệp đã chuẩn bị và vẫn thu được lợi nhuận cao nhất thì xí nghiệp phải sản xuất m chiếc bánh nướng và n chiếc bánh dẻo, với \(m,n\) là các số tự nhiên. Tính giá trị \(\frac{{m + n}}{6}\).
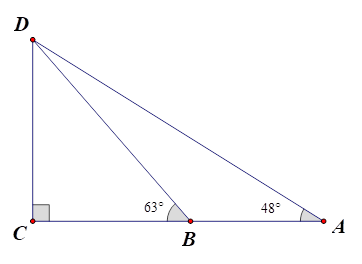
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24 m, \(\widehat {CBD} = 63^\circ ,\widehat {CAD} = 48^\circ \) (tham khảo hình vẽ). Tính chiều cao của khối tháp (làm tròn kết quả đến hàng phần mười).
Cho hình thoi \(ABCD\) tâm \(O\) có cạnh bằng 4 và \(\widehat {ABD} = 60^\circ \). Gọi \(I\)là điểm thỏa mãn \(2\overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \). Tính tích vô hướng \(\overrightarrow {AO} .\overrightarrow {BI} \).
Hai người muốn dùng dây kéo một khối gỗ nổi trên mặt nước đi dọc theo bờ sông (như hình vẽ minh họa). Người thứ nhất dùng lực kéo 300 N. Hỏi người thứ hai cần dùng lực bao nhiêu để kéo được khúc gỗ đi dọc theo bờ sông (làm tròn đến hàng đơn vị).