Bộ 5 đề thi cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 03
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tập hợp \(X = \left\{ {1;2;3;4} \right\}\). Câu nào sau đây đúng?
Số tập con của \(X\) là \(16\).
Số tập con của \(X\) gồm có \(2\) phần tử là \(8\).
Số tập con của \(X\) chứa số \(1\) là \(6\).
Số tập con của \(X\) gồm có \(3\) phần tử là \(2\).
Cho \(A = \left\{ {\left. {x \in \mathbb{N}} \right|\left( {2x - {x^2}} \right)\left( {2{x^2} - 3x - 2} \right) = 0} \right\};B = \left\{ {\left. {n \in {\mathbb{N}^*}} \right|3 < {n^2} < 30} \right\}\). Khi đó tập hợp \(A \cap B\)bằng:
\(\left\{ {2;4} \right\}.\)
\(\left\{ 2 \right\}.\)
\(\left\{ {4;5} \right\}.\)
\(\left\{ 3 \right\}.\)
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(2x - 5y + 3z \le 0\).
\(3{x^2} + 2x - 4 > 0\).
\(2{x^2} + 5y > 3\).
\(2x + 3y < 5\).
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không gạch trong hình vẽ sau?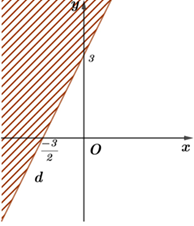
\(2x - y \ge - 3\).
\(2x - y \le - 3.\)
\(2x - y < - 3.\)
\(2x - y > - 3.\)
Cho ba điểm phân biệt\[A,B,C\]. Trong các khẳng định sau, khẳng định nào sai?
\[\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \].
\[\overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \].
\[\overrightarrow {CA} + \overrightarrow {BC} = \overrightarrow {BA} \].
\[\overrightarrow {CB} + \overrightarrow {AC} = \overrightarrow {BA} \].
Cho ba điểm phân biệt \(A,B,C\). Nếu \(\overrightarrow {AB} = - 3\overrightarrow {AC} \) thì đẳng thức nào dưới đây đúng?
\(\overrightarrow {BC} = - 4\overrightarrow {AC} \).
\(\overrightarrow {BC} = - 2\overrightarrow {AC} \).
\(\overrightarrow {BC} = 2\overrightarrow {AC} \).
\(\overrightarrow {BC} = 4\overrightarrow {AC} \).
Gọi \(M,\;N\) lần lượt là trung điểm của các cạnh \(AB,\;AC\) của tam giác đều \(ABC\). Đẳng thức nào sau đây đúng?
\(\overrightarrow {MA} = \overrightarrow {MB} .\)
\(\overrightarrow {AB} = \overrightarrow {AC} .\)
\(\overrightarrow {MN} = \overrightarrow {BC} .\)
\(\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {MN} } \right|.\)
Cho hình thoi tâm O, cạnh bằng a và \(\widehat A = 60^\circ \). Kết luận nào sau đây là đúng?
\(\left| {\overrightarrow {AO} } \right| = \frac{{a\sqrt 3 }}{2}\).
\(\left| {\overrightarrow {OA} } \right| = a\).
\(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right|\).
\(\left| {\overrightarrow {OA} } \right| = \frac{{a\sqrt 2 }}{2}\).
Cho giá trị gần đúng của \[\frac{8}{{17}}\] là \[0,47\]. Sai số tuyệt đối của số \[0,47\] là:
\[0,001\].
\[0,002\].
\[0,003\].
\[0,004\].
Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được: \[\sqrt 8 = 2,828427125\].Giá trị gần đúng của \[\sqrt 8 \] chính xác đến hàng phần trăm là:
\(2,80.\)
\(2,81.\)
\(2,82.\)
\(2,83.\)
Cho mẫu số liệu sau: \(4;5;6;7;8;4;9;4;3;5\). Khoảng tứ phân vị của mẫu là
\(3.\)
\(4.\)
\(5.\)
\(7.\)
Cho mẫu số liệu sau: \(4;5;6;7;8;4;9;4;3;5\). Phương sai của mẫu số liệu là
\(5,5.\)
\(3,45.\)
\(1,85.\)
\(7.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}2x + y \le 4\\x + 2y \le 4\\x \ge 0\\y \ge 0\end{array} \right.\).
Hệ trên không là hệ bất phương trình bậc nhất hai ẩn.
Cặp \(\left( {4;1} \right)\) thuộc miền nghiệm của hệ.
Biểu diễn miền nghiệm của hệ là phần được tô đậm như trong hình dưới đây
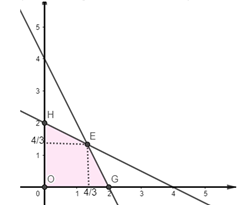
Gọi \(\left( {x;y} \right)\) thỏa mãn hệ. Biểu thức \(F\left( {x;y} \right) = 3x + 4y + 2024\) đạt giá trị lớn nhất tại \(\left( {0;2} \right)\).
Quan sát đồ thị hàm số bậc hai \(y = f(x)\) ở Hình
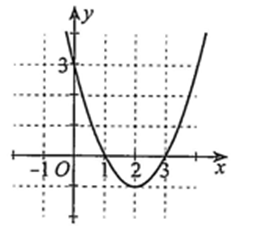
Khi đó:
\(a > 0.\)
Toạ độ đỉnh \(I(2; - 1)\), trục đối xứng \(x = 2.\)
Đồng biến trên khoảng \(( - \infty ;2)\); Nghịch biến trên khoảng \((2; + \infty )\).
\(x\) thuộc các khoảng \(( - \infty ;1)\) và \((3; + \infty )\) thì \(f(x) > 0\).
Cho góc α \(\left( {0^\circ < \alpha < 180^\circ } \right)\) thỏa mãn \(\cot \alpha = - \frac{1}{3}\).
\(\tan \alpha = 3\).
\(\alpha \) là góc tù.
\(\sin \alpha = \frac{{3\sqrt {10} }}{{10}}\).
Giá trị của biểu thức \(P = \frac{{2\sin \alpha - 3\cos \alpha }}{{3\sin \alpha + 2\cos \alpha }}\) bằng \(\frac{1}{5}\).
Cho hình bình hành \(ABCD\). Gọi \(I,J\) lần lượt là trung điểm \(BC\) và \[CD\]. Khi đó:
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
\(\overrightarrow {AI} = \overrightarrow {AC} + \overrightarrow {AB} \).
\(\overrightarrow {AI} = \overrightarrow {AB} + \frac{3}{2}\overrightarrow {AD} \).
\(\overrightarrow {AJ} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} .\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Biểu đồ dưới đây cho biết tăng trưởng GDP trong 9 tháng đầu năm trong giai đoạn 2011 – 2018 của Việt Nam.
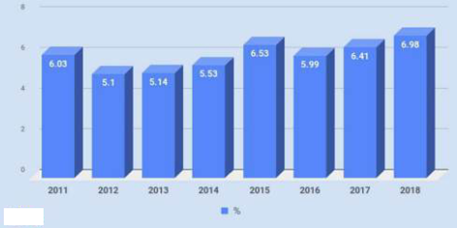
Cho biết năm nào tăng trưởng GDP trong 9 tháng đầu năm trong giai đoạn 2011 – 2018 là cao nhất?
Khi một quả bóng được đá lên nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết quỹ đạo của quả bóng là một đường parabol trong mặt phẳng toạ độ \(Oxy\) có phương trình \(h = a{t^2} + bt + c\left( {a < 0} \right)\) trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1m và sau 1 giây thì nó đạt độ cao \(6,5{\rm{m}}\);sau 4 giây nó đạt độ cao \(5{\rm{m}}\). Tính tổng \(2a + b + c\).
Cho hình bình hành \(ABCD\) có \(\hat A = 60^\circ \) và \(AB = 5,AD = 8\). Tính độ dài đường chéo \(AC\)(kết quả làm tròn đến hàng đơn vị).
Một tháp nước cao 30 m ở trên đỉnh của một ngọn đồi. Từ tháp đến chân ngọn đồi dài 120 m và người ta quan sát thấy góc tạo thành giữa đỉnh và chân tháp là \(8^\circ \). Gọi \(\alpha \) góc nghiêng của ngọn đồi so với phương ngang. Tính gần đúng \(\tan \alpha \) (kết quả được làm tròn đến hàng phần trăm).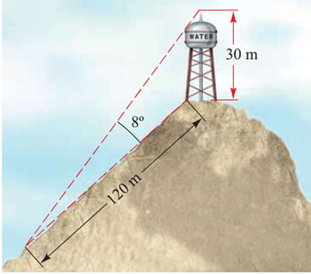
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MB} ,\overrightarrow {{F_2}} = \overrightarrow {MA} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Biết cường độ của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) lần lượt là 28 N và 45 N. Tìm cường độ của lực \(\overrightarrow {{F_3}} \) biết \(\widehat {AMB} = 90^\circ \).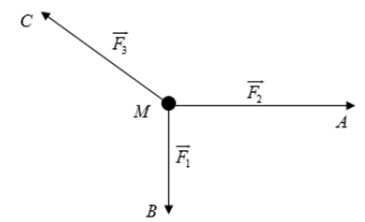
Một chiếc xe ô tô con bị mắc kẹt trong bùn lầy. Để kéo xe ra, người ta dùng xe tải kéo bằng cách gắn một đầu dây cáp kéo xe vào đầu xe ô tô con và móc đầu còn lại vào phía sau của xe tải. Khi kéo, xe tải tạo ra một lực \({F_1}\) có độ lớn (cường độ) là 2000 N theo phương ngang lên xe ô tô con. Ngoài ra, có thêm một người đẩy phía sau ô tô con, tạo ra lực \(\overrightarrow {{F_2}} \) có độ lớn là 300 N lên xe. Các lực này đều được biểu diễn bằng vectơ (như hình vẽ) sao cho \(\left( {\overrightarrow {{F_1},} \overrightarrow {{F_2}} } \right) = 5^\circ \). Độ lớn tổng lực tổng hợp lên xe ô tô con là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị)?