Bộ 5 đề thi cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 04
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mệnh đề đảo của mệnh đề “Nếu tứ giác \(ABCD\) là hình chữ nhật thì nó có hai đường chéo bằng nhau” là
Nếu tứ giác \(ABCD\) có hai đường chéo bằng nhau thì nó không là hình chữ nhật.
Nếu tứ giác \(ABCD\) có hai đường chéo bằng nhau thì nó là hình chữ nhật.
Nếu tứ giác \(ABCD\) là hình chữ nhật thì nó không có hai đường chéo bằng nhau.
Nếu tứ giác \(ABCD\) không có hai đường chéo bằng nhau thì nó không là hình chữ nhật.
Cho hai tập hợp \(A = \left[ { - 1;3} \right)\) và \(B = \left( {2;5} \right]\). Khẳng định nào sau đây sai?
\(A \cap B = \left( {2;3} \right)\).
\(A \cup B = \left[ { - 1;5} \right]\).
\(B\backslash A = \left( {3;5} \right]\).
\(A\backslash B = \left[ { - 1;2} \right]\).
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình \(3x - 5y < 2\).
\(Q\left( { - 2; - 3} \right)\).
\(M\left( {2;1} \right)\).
\(P\left( {4;2} \right)\).
\(N\left( {1; - 2} \right)\).
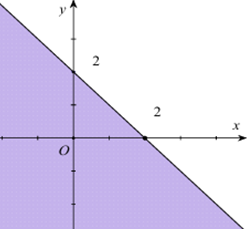
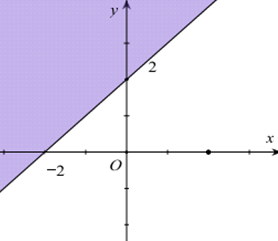
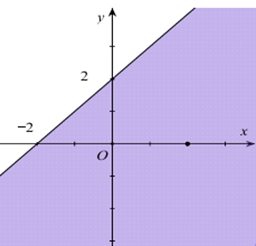
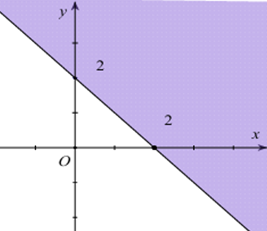
Miền nghiệm của bất phương trình \(x + y \le 2\) là phần tô đậm trong hình vẽ nào sau đây?
Cho ba điểm M, N, P thẳng hàng, trong đó N nằm giữa hai điểm M và P. Khi đó cặp vectơ nào sau đây cùng hướng?
\(\overrightarrow {MN} \) và \(\overrightarrow {MP} \).
\(\overrightarrow {MN} \) và \(\overrightarrow {PN} \).
\(\overrightarrow {MP} \) và \(\overrightarrow {PN} \).
\(\overrightarrow {NP} \) và \(\overrightarrow {NM} \).
Cho tam giác \(ABC\) có \(AB = AC = a,\widehat {BAC} = 60^\circ \). Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} .\)
\(\overrightarrow {AB} .\overrightarrow {AC} = 2{a^2}.\)
\(\overrightarrow {AB} .\overrightarrow {AC} = - \frac{{{a^2}\sqrt 3 }}{2}\).
\(\overrightarrow {AB} .\overrightarrow {AC} = - \frac{{{a^2}}}{2}\).
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\).
Cho tam giác \(ABC\) đều cạnh \(a\) và \(G\) là trọng tâm. Gọi \(I\) là trung điểm của \(AG\).
Độ dài của vectơ là
\[a\frac{{\sqrt {21} }}{6}\].
\[a\frac{{\sqrt {21} }}{3}\].
\[a\frac{{\sqrt 3 }}{6}\].
\[a\frac{{\sqrt 3 }}{2}\].
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 9\), \(BC = 5\). Tính \(\overrightarrow {AB} .\overrightarrow {AC} \)
\(9\).
\(81\).
\(3\).
\(5\).
Viết số quy tròn số gần đúng \(b = 3257,6254\) với độ chính xác \(d = 0,01\).
\(b \approx 3257,63\).
\(b \approx 3257,62\).
\(b \approx 3257,6\).
\(b \approx 3257,7\).
Số \(\overline a \) được cho bởi giá trị gần đúng \(a = 5,7824\) với sai số tương đối không vượt quá \(0,05\% \). Khi đó sai số tuyệt đối của \(a\) không vượt quá
\(0,0028912\).
\(0,0027912\).
\(0,0026912\).
\(0,0025912\).
Mốt của mẫu số liệu trên là
\(15\).
\(4\)và \(6\).
\(4\).
\(6\).
Độ lệch chuẩn về số giờ học thêm của 10 học sinh trên là
\(6\).
\(15\).
\(12\).
\(3,5\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + 5y \ge - 4\\x + 3y \le 9\\3x - 2y \ge - 6\\x \le 3\end{array} \right.\).
\(\left( {0;0} \right)\) là một nghiệm của hệ bất phương trình.
\(\left( { - 1;2} \right)\) là một nghiệm của hệ bất phương trình.
Miền nghiệm của hệ bất phương trình là miền tam giác đều.
\(x = 3;y = 2\) là nghiệm của hệ bất phương trình trên sao cho \(F = 3x - y\) đạt giá trị lớn nhất.
Cho hàm số \(y = {x^2} + 2x\). Khi đó:
Tọa độ đỉnh \(I\) của parabol: \(I( - 1; - 1){\rm{. }}\)
Bảng biến thiên:
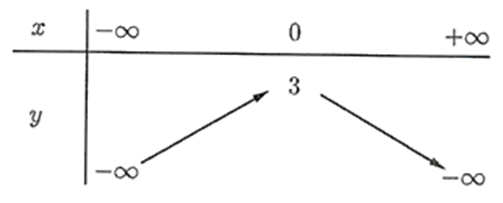
Hàm số đã cho đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Hàm số không có giá trị lớn nhất.
Cho \(\sin \alpha = \frac{1}{3}\) với \(90^\circ < \alpha < 180^\circ \).
Giá trị \(\sin \alpha .\cos \alpha < 0\).
Có \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\).
Có \(\tan \alpha = \frac{{\sqrt 2 }}{4}\).
Giá trị biểu thức \(\frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \sqrt 2 \cot \alpha }} = \frac{2}{5}\).
Cho tam giác \(ABC\) có \(G\) là trọng tâm. Gọi \(D\) là điểm đối xứng của \(B\) qua \(G,M\) là trung điểm của \(BC\). Khi đó:
\(\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {GD} \).
\(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
\(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BN} \).
\(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} {\rm{. }}\)
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một cửa hàng nhân dịp Noel đã đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm \(10\% \) so với giá ban đầu. Biết giá gói đầu là 60000 đồng. Bạn An có 500000 đồng. Hỏi bạn An có thể mua tối đa bao nhiêu gói kẹo?
Một cửa hàng kinh doanh giày và giá để nhập một đôi giày là 40 đô la. Theo nghiên cứu của bộ phận kinh doanh thì nếu cửa hàng bán mỗi đôi giày với giá \(x\) đô la thì mỗi tháng sẽ bán được \(120 - x\) đôi giày. Hỏi cửa hàng bán giá bao nhiêu đô la cho một đôi giày để có thể thu lãi cao nhất trong tháng.
Cho tam giác \(ABC\) có \(AB = 5,AC = 8,\hat A = 60^\circ \). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\) (kết quả làm tròn đến hàng phần trăm).
Thành phố Hải Đông dự định xây dựng một trạm nước sạch để cung cấp cho hai khu dân cư \(A\) và \(B\). Trạm nước sạch đặt tại vị trí \(C\) trên bờ sông. Biết \(AB = 3\sqrt {17} \;{\rm{km}}\), khoảng cách từ \(A\) và \(B\) đến bờ sông lần lượt là \(AM = 3\;{\rm{km}},BN = 6\;{\rm{km}}\) (hình vẽ). Gọi \(T\) là tổng độ dài đường ống từ trạm nước đến \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\) (kết quả làm tròn đến hàng phần trăm).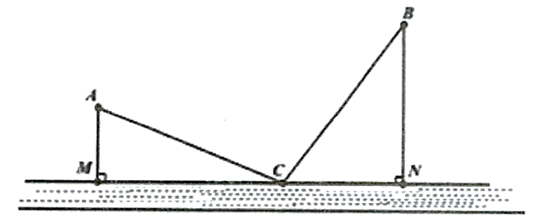
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\). Cho biết \(\left| {\overrightarrow {{F_3}} } \right| = \sqrt 3 \left| {\overrightarrow {{F_2}} } \right| = \sqrt 3 \left| {\overrightarrow {{F_1}} } \right|\). Khi vật đứng yên thì \(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right) = \alpha ^\circ \). Giá trị của \(\alpha \) bằng bao nhiêu?
Một vật có trọng lượng \(P = 20{\rm{N}}\) được đặt trên một mặt phẳng nghiêng với góc nghiêng \(\alpha = 30^\circ \). Khi đó độ lớn của các lực \(\overrightarrow N ,\overrightarrow {{F_p}} \) lần lượt là \(a\;\left( {\rm{N}} \right)\), \(b\;\left( {\rm{N}} \right)\). Tính \(a + b\) (kết quả làm tròn đến hàng phần trăm).