Bộ 10 đề thi Giữa kì 1 Toán 10 Chân trời sáng tạo có đáp án - Đề 4
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Câu nào dưới đây là một mệnh đề?
“Tháng 8 dương lịch có 31 ngày.”;
“Số 2 022 có chia hết cho 20 không?”;
“Vườn hoa này đẹp quá!”;
“Cảnh báo đường trơn, hãy lái xe cẩn thận!”.
Viết mệnh đề sau bằng cách dùng kí hiệu \(\forall \) hoặc \(\exists \): “Cho hai số thực khác nhau bất kì, luôn tồn tại một số hữu tỉ nằm giữa hai số thực đã cho”.
“”;
“”;
“”;
“”.
Mệnh đề nào sau đây là mệnh đề sai?
Một tam giác là tam giác đều khi và chỉ khi nó có hai đường trung tuyến bằng nhau và một góc bằng \(60^\circ \);
Một tam giác là tam giác vuông khi và chỉ khi nó có bình phương một cạnh bằng tổng các bình phương hai cạnh còn lại;
Một tứ giác là hình chữ nhật khi và chỉ khi nó có ba góc vuông;
Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}| - 8 \le x < 2} \right\}\). Viết tập hợp \(A\) dưới dạng kí hiệu đoạn, khoảng hoặc nửa khoảng ta được
\(A = \left\{ { - 8;\,\,2} \right\}\);
\(A = \left( { - 8;\,\,2} \right)\);
\(A = \left[ { - 8;\,\,2} \right]\);
\(A = \left[ { - 8;\,\,2} \right)\).
Cho ba tập hợp \(X = \left\{ {0;\,\,10;\,\,20;\,\,30} \right\}\), \(Y = \left\{ {x \in \mathbb{N}|x\,\, \vdots \,\,10,\,x < 50} \right\}\) và \(Z = \left\{ {10;\,20;\,\,30;\,\,40;\,\,50} \right\}\). Khẳng định nào sau đây đúng?
\(X = Y\);
\(Y = Z\);
\[Y \subset Z\];
\(X \subset Y\).
Chọn khẳng định sai trong các khẳng định sau:
\(\mathbb{N} \cap \mathbb{Z} = \mathbb{N}\);
\(\mathbb{Q} \cup \mathbb{R} = \mathbb{R}\);
\(\mathbb{Q} \cap {\mathbb{N}^*} = {\mathbb{N}^*}\);
\(\mathbb{Q} \cup {\mathbb{N}^*} = {\mathbb{N}^*}\).
Ký hiệu nào sau đây để chỉ \(\sqrt 5 \) không phải là số hữu tỉ?
\(\sqrt 5 \in \mathbb{Q}\);
\(\sqrt 5 \notin \mathbb{Q}\);
\(\sqrt 5 \in \mathbb{N}\);
\(\sqrt 5 \not\subset \mathbb{Q}\).
Cho hai tập hợp \(A = \left[ { - 2;\,3} \right]\) và \(B = \left( {0;\,\, + \infty } \right)\). Tập hợp \(A \cap B\) là
\(\left[ { - 2;\,\, + \infty } \right)\);
\(\left( {0;\,\,3} \right]\);
\(\left[ {0;\,\,3} \right]\);
\(\left( {0;\,\,3} \right)\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\({x^2} + 3{y^2} \ge 9\);
\({3^3}x + {4^2}y > 25\);
\(\frac{2}{x} + \frac{3}{y} < 5\);
\( - xy + {3^2}y < 0\).
Bất phương trình nào sau đây nhận \(\left( {1;\,\, - 2} \right)\) là một nghiệm?
\(5x + 3y > 1\);
\(4x - 7y < 10\);
\(7x + y \ge 2\);
\(x - 9y \le 7\).
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(x + 5y > 2\) là
nửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (kể cả bờ \(d\));
nửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) không chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (kể cả bờ \(d\));
mửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (không kể bờ \(d\));
nửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) không chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (không kể bờ \(d\)).
Hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + 5{y^2} \ge 1\\ - x + y < 2\end{array} \right.\);
\(\left\{ \begin{array}{l}x{y^2} < 1\\x + 2y > - 4\end{array} \right.\);
\(\left\{ \begin{array}{l}\frac{1}{{3x}} + \frac{1}{y} > 1\\\frac{2}{x} + y > 3\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 2y < 1\\{5^2}x + 7y > 2\end{array} \right.\).
Cặp số nào sau đây là một nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\2x + y < 8\\ - x + 3y \ge 6\end{array} \right.\)?
\(\left( {2;\, - 3} \right)\);
\(\left( {4;\,\,1} \right)\);
\(\left( { - 2;\,\, - 2} \right)\);
\(\left( { - 1;\,\,5} \right)\).
Cho góc \(\alpha \) và \(\beta \) thỏa mãn . Mối liên hệ của hai góc đó là
\(\alpha \) và \(\beta \) bù nhau;
\(\alpha \) và \(\beta \) phụ nhau;
\(\alpha \) và \(\beta \) bằng nhau;
\(\alpha \) và \(\beta \) không có mối liên hệ.
Cho góc \(\alpha \)\(\left( {0^\circ \le \alpha \le 180^\circ } \right)\) thỏa mãn \(\cos \alpha = \frac{1}{3}\) . Giá trị của \(\sin \alpha \) bằng
\(\frac{{\sqrt 3 }}{3}\);
\(\frac{2}{3}\);
\(\frac{{2\sqrt 2 }}{3}\);
\(\frac{{ - 2\sqrt 2 }}{3}\).
Giá trị của biểu thức \(H = \sin 90^\circ + \cos 18^\circ + \sin 32^\circ + \cos 162^\circ - \sin 148^\circ \) là
0;
1;
\[\sqrt 3 \];
– 1.
Cho tam giác \(ABC\) với \(BC = a,\,\,AC = b,\,\,AB = c\). Khẳng định nào sau đây là sai?
\({a^2} = {b^2} + {c^2} - 2bc \cdot \cos A\);
\({a^2} = {b^2} + {c^2}\);
\({b^2} = {c^2} + {a^2} - 2ca \cdot \cos B\);
\({c^2} = {b^2} + {a^2} - 2ba \cdot \cos C\).
Cho tam giác \(ABC\) với \(BC = a,\,\,AC = b,\,\,AB = c\), \(p = \frac{{a + b + c}}{2}\). Khi đó, diện tích \(S\) của tam giác \(ABC\) là
\[S = \frac{1}{2}\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \];
\[S = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)\];
\[S = ac\sin B\];
\[S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \].
Cho tam giác \(ABC\) có \(AB = 2,\,\,AC = 2\sqrt 2 ,\,\cos \left( {B + C} \right) = - \frac{{\sqrt 2 }}{2}\). Độ dài cạnh \(BC\) là
2;
4;
12;
20.
Cho tam giác \(ABC\) có \[AB = 10,\,\,\widehat C = 45^\circ ,\,\,\widehat B = 60^\circ \]. Độ dài cạnh \(AC\) là
\(5\sqrt 3 \);
\(5\sqrt 6 \);
\(10\sqrt 3 \);
\(10\sqrt 6 \).
Giải tam giác là
tìm độ dài các cạnh còn lại của tam giác khi biết số đo các góc;
tìm số đo các góc còn lại của tam giác khi biết độ dài các cạnh;
tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó;
tính diện tích tam giác bằng các cách khác nhau.
Cho tam giác \(ABC\) nội tiếp đường tròn có bán kính \(R = 12\) và\(\,\widehat C = 30^\circ \). Độ dài cạnh \(AB\) bằng
6;
12;
\(12\sqrt 3 \);
24.
Hai vectơ được gọi là bằng nhau nếu
chúng có cùng hướng và cùng độ dài;
chúng có hướng ngược nhau và cùng độ dài;
chúng có cùng độ dài;
chúng có cùng phương và cùng độ dài.
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Số các vectơ khác vectơ-không, ngược hướng với vectơ \(\overrightarrow {OA} \), có điểm đầu và điểm cuối là các đỉnh của lục giác đều là
2;
3;
4;
6.
Cho bốn điểm \(A,\,\,B,\,\,C,\,\,D\) phân biệt. Khẳng định nào sau đây là đúng?
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \);
\(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {DA} \);
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {CD} + \overrightarrow {DA} \);
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CD} + \overrightarrow {CB} \).
Cho hình bình hành \(ABCD\) có tâm \(O\). Tìm khẳng định sai?
\(\overrightarrow {AO} + \overrightarrow {BO} = \overrightarrow {BC} \);
\(\overrightarrow {AO} + \overrightarrow {DC} = \overrightarrow {BO} \);
\(\overrightarrow {AO} + \overrightarrow {CD} = \overrightarrow {BO} \);
\(\overrightarrow {AO} - \overrightarrow {BO} = \overrightarrow {DC} \).
Cho hình chữ nhật \(ABCD\) có \(AB = 9,\,\,AD = 3\). Khi đó, \(\left| {\overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {CD} } \right|\) bằng
\(3\sqrt {10} \);
\(12\);
\(10\sqrt 3 \);
\(15\).
Cho tam giác \(ABC\). Vị trí của điểm \(M\) sao cho \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) là
\(M\) là đỉnh thức tư của hình bình hành \(CABM\);
\(M\) là đỉnh thức tư của hình bình hành \(CBAM\);
\(M\) trùng \(B\);
\(M\) trùng \(C\).
Cho đoạn thẳng \(AB\) và \(O\) là trung điểm của \(AB\). Khẳng định nào sau đây là đúng?
\(\overrightarrow {AB} = 2\overrightarrow {OA} \);
\(\overrightarrow {AB} = 2\overrightarrow {OB} \);
\(\overrightarrow {AB} = - 2\overrightarrow {OB} \);
\(\overrightarrow {AO} = 2\overrightarrow {AB} \).
Cho ba điểm phân biệt \(A,\,\,B,\,\,C\). Nếu \(\overrightarrow {AB} = - 3\overrightarrow {AC} \) thì đẳng thức nào sau đây là đúng?
\(\overrightarrow {BC} = - 4\overrightarrow {AC} \);
\(\overrightarrow {BC} = - 2\overrightarrow {AC} \);
\(\overrightarrow {BC} = 2\overrightarrow {AC} \);
\(\overrightarrow {BC} = 4\overrightarrow {AC} \).
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(G\) là trọng tâm của tam giác, Khi đó \(\overrightarrow {AM} = ...\overrightarrow {GM} \). Số thích hợp điền vào chỗ chấm là
\( - 3\);
\(\frac{3}{2}\);
\(\frac{{ - 3}}{2}\);
3.
Cho tam giác \[ABC\] và điểm \[M\] thuộc cạnh \(BC\) sao cho \[BM = 3MC\]. Phân tích vectơ \[\overrightarrow {AM} \] theo các vectơ \[\overrightarrow {AB} \], \[\overrightarrow {AC} \] ta được
\(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \);
\(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \);
\(\overrightarrow {AM} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \);
\(\overrightarrow {AM} = \frac{5}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \).
Phát biểu nào sau đây là đúng?
Nếu \(\overrightarrow a ,\,\,\overrightarrow b \) khác \(\overrightarrow 0 \) và \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) < 90^\circ \) thì \(\overrightarrow a \cdot \overrightarrow b < 0\);
Nếu \(\overrightarrow a ,\,\,\overrightarrow b \) khác \(\overrightarrow 0 \) và \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) > 90^\circ \) thì \(\overrightarrow a \cdot \overrightarrow b > 0\);
Nếu \(\overrightarrow a ,\,\,\overrightarrow b \) khác \(\overrightarrow 0 \) và \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) < 90^\circ \) thì \(\overrightarrow a \cdot \overrightarrow b > 0\);
Nếu \(\overrightarrow a ,\,\,\overrightarrow b \) khác \(\overrightarrow 0 \) và \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) \ne 90^\circ \) thì \(\overrightarrow a \cdot \overrightarrow b < 0\).
Cho tam giác \[ABC\] vuông cân tại \(A\) có \(BC = 4a\). Tích vô hướng \(\overrightarrow {CA} \cdot \overrightarrow {CB} \) bằng
\(8{a^2}\);
\(a\);
\(\frac{{{a^2}\sqrt 2 }}{2}\);
\({a^2}\sqrt 2 \).
Cho hình vuông \(ABCD\). Góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \) bằng
\(45^\circ \);
\[135^\circ \];
\(50^\circ \);
\(90^\circ \).
II. Tự luận (3 điểm)
(1 điểm) Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất, biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900 ?
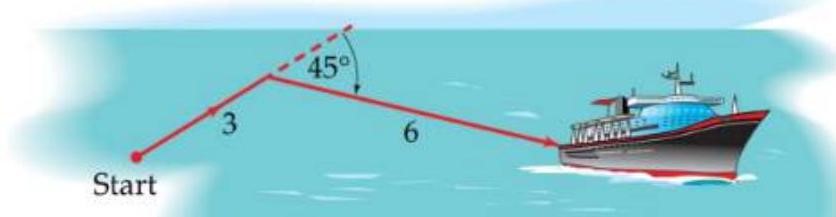
(1 điểm) Một chiếc thuyền chạy trên đường thẳng được 3 km thì rẽ \(45^\circ \) và đi tiếp thêm 6 km nữa (như hình vẽ). Khi đó chiếc thuyền cách điểm xuất phát của nó bao xa? (làm tròn đáp án đến 2 chữ số thập phân sau dấu phẩy)
(1 điểm) Cho tứ giác \(ABCD\) có \[A{B^2} + C{D^2} = B{C^2} + A{D^2}\]. Chứng minh rằng hai đường chéo \(AC\) và \(BD\) của tứ giác \(ABCD\) vuông góc với nhau.