Bộ 5 đề thi giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 3
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi!
b) Số \[15\] là số nguyên tố.
c) Tổng các góc của một tam giác là \(180^\circ \).
d) \[3\]là số nguyên dương.
\[3\].
\[2\].
\[4\
\[1\].
Cho tập hợp \(B = \left\{ {x \in \mathbb{R}|a \le x < b} \right\}\). Mệnh đề nào dưới đây đúng?
\(B = \left( {a;\,b} \right]\).
\[B = \left[ {a;\,b} \right)\].
\(B = \left[ {a;\,b} \right]\).
\[B = \left( {a;\,b} \right)\].
Điểm nào sau đây thuộc miền nghiệm của bất phương trình \(x + 5y - 3 < 0\)?
\[M\left( {1;2} \right)\].
\[N\left( { - 1;\,7} \right)\].
\[P\left( {0;\,2} \right)\].
\[Q\left( { - 8;\,1} \right)\].
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ {\begin{array}{*{20}{c}}{x + {y^2} > 4}\\{ - 3x - 5y \le - 6}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{ - 3x + y \le - 1}\\{\sqrt 5 x - 7y > 5}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{3x + y \ge 9}\\{\frac{2}{x} - 3y \le 1}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{{x^3} + y > 4}\\{ - x - y \le 100}\end{array}} \right.\).
Giá trị \(\cos 45^\circ + \sin 45^\circ \) bằng bao nhiêu?
\[1\].
\(\sqrt 2 \).
\(\sqrt 3 \).
\[0\].
Cho tam giác ABC có \(AB = 5\,{\rm{cm}}\), \(AC = 8\,{\rm{cm}}\) và \(BC = 7\,{\rm{cm}}\) . Số đo góc \[A\] bằng
\[60^\circ \].
\[30^\circ \].
\[120^\circ \].
\[90^\circ \].
Cho tam giác \(ABC\), có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là các đỉnh \(A,{\rm{ }}B,{\rm{ }}C\).
\(3\).
\(4\).
\(5\).
\(6\).
Cho ba điểm \[M,N,P\] thẳng hàng, trong đó điểm \[N\] nằm giữa hai điểm \[M\] và \[P\]. Khi đó cặp vectơ nào sau đây cùng hướng?
\[\overrightarrow {MN} \] và \[\overrightarrow {PN} \].
\[\overrightarrow {MN} \] và \[\overrightarrow {MP} \].
\[\overrightarrow {MP} \] và \[\overrightarrow {PN} \].
\[\overrightarrow {NM} \] và \[\overrightarrow {NP} \].
Cho hình bình hành \[ABCD\]. Vectơ tổng \[\overrightarrow {CB} + \overrightarrow {CD} \] bằng
\(\overrightarrow {CA} \).
\(\overrightarrow {BD} \).
\(\overrightarrow {AC} \).
\(\overrightarrow {DB} \).
Với giá trị thực nào của \[x\] mệnh đề chứa biến \[P\left( x \right):2x - 5 > 0\] là mệnh đề đúng?
\[x = 2023\].
\[x = - 23\].
\[x = 2\].
\[x = 0\].
Cho hai tập hợp \(A = \left\{ {x \in \left. \mathbb{R} \right|x - 1 > 0} \right\}\(A \cup B = \left( { - \infty ; + \infty } \right) = \mathbb{R}\)\) và \(B = \left\{ {x \in \left. \mathbb{R} \right|x - 2022 \le 0} \right\}\). Khi đó: \(A \cup B\) là
\(\left( {1;2022} \right]\).
\(\left( {1; + \infty } \right)\).
\(\mathbb{R}\).
\(\left[ {2022; + \infty } \right)\).
Cho \(\tan \alpha - \cot \alpha = 3.\) Tính giá trị của biểu thức sau: \(A = {\tan ^2}\alpha + {\cot ^2}\alpha \).
\(A = 12\).
\(A = 11\).
\(A = 13\).
\(A = 5\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho bất phương trình bậc nhất hai ẩn: \(x + y - 2 \ge 0\).
a) Đường thẳng \(d:x + y - 2 = 0\) đi qua hai điểm \(A\left( {0;2} \right)\) và \(B\left( {2;0} \right)\).
b) Gốc toạ độ \(O\left( {0;0} \right)\) không thuộc miền nghiệm của bất phương trình \(x + y - 2 \ge 0\).
c) \(M\left( {1;4} \right)\) thuộc miền nghiệm của bất phương trình \(x + y - 2 \ge 0\).
d) Phần bị gạch trong hình bên dưới (bao gồm cả bờ \(d:x + y - 2 = 0\)) là miền nghiệm của bất phương trình \(x + y - 2 \ge 0\).

Cho tam giác \(ABC\) có \(M,N\) lần lượt là trung điểm của \(AC,BC\); \(AB = a\).
a) \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN = \frac{1}{2}AB\).
b) \(\overrightarrow {NB} = \overrightarrow {CN} \).
c) \(\overrightarrow {CM} - \overrightarrow {CN} = \overrightarrow {MN} \).
d) \(\left| {\overrightarrow {CM} - \overrightarrow {NB} } \right| = \frac{a}{2}\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho mệnh đề \(P:\) “\({x^2} - 3x + 4 = 0\) vô nghiệm” và các mệnh đề sau:
“\({x^2} - 3x + 4 = 0\) có nghiệm”.
“\({x^2} - 3x + 4 = 0\) có hai nghiệm phân biệt”.
“\({x^2} - 3x + 4 = 0\) không vô nghiệm”.
Có bao nhiêu phát biểu là phủ định của mệnh đề \(P\)?
Cho \(\tan \alpha = 1\). Tính \(B = \frac{{{{\sin }^2}\alpha + 1}}{{2{{\cos }^2}\alpha - {{\sin }^2}\alpha }}\).
Một tam giác có độ dài ba cạnh là 52, 56, 60. Gọi \(R,r\) lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó \(R \cdot r\) bằng bao nhiêu?
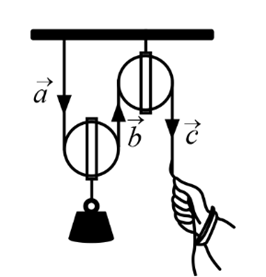
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) và \(\overrightarrow c \) như hình vẽ dưới. Trong các vectơ đó, cho biết có bao nhiêu cặp vectơ ngược hướng?
PHẦN II. TỰ LUẬN
Lớp 10A chuẩn bị lập danh sách thi học sinh giỏi ba môn Toán, Văn, Anh. Lớp có 16 bạn giỏi môn Toán, 17 bạn giỏi môn Văn, 18 bạn giỏi môn Anh. Trong đó có 4 bạn giỏi đúng hai môn Toán và Văn, 5 bạn chỉ giỏi hai môn Văn và Anh, giỏi đúng hai môn Toán và Anh có 5 bạn. Biết rằng có 3 bạn giỏi cả ba môn và học sinh giỏi ít nhất một môn sẽ có tên trong danh sách thi học sinh giỏi. Hỏi danh sách có bao nhiêu học sinh?
Trong năm nay, một cửa hàng kinh doanh xe máy dự định kinh doanh hai loại xe máy: xe máy Lead và xe máy Vision, với số vốn ban đầu không vượt quá 36 tỉ đồng. Giá nhập về 1 chiếc xe máy Lead là 40 triệu đồng, lợi nhuận dự kiến là \(5\) triệu đồng một chiếc. Giá nhập về 1 chiếc xe máy Vision là 30 triệu đồng, lợi nhuận dự kiến là \(3,2\) triệu đồng một chiếc. Cửa hàng ước tính rằng tổng nhu cầu thị trường không vượt quá 1100 chiếc xe cả hai loại và nhu cầu xe Lead không vượt quá \(1,5\) lần nhu cầu xe Vision.
Lợi nhuận có thể thu được lớn nhất của cửa hàng là bao nhiêu tiền?
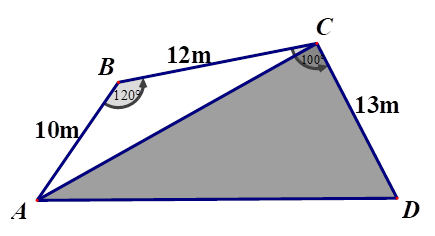
Hướng tới kỉ niệm 70 năm thành lập trường THPT TCV, nhà trường dự định bố trí một phần diện tích trong khuôn viên nhà trường để trưng bày các sản phẩm lưu giữ những kỉ niệm của Đoàn Thanh Niên qua các thời kỳ, phần diện tích đó có hình dạng là một tứ giác ABCD (hình vẽ).
Biết \(AB = 10\,\,{\rm{m}},\,BC = 12\,{\rm{m}},\,CD = 13\,\,{\rm{m}},\,\widehat {ABC} = 120^\circ ,\,\widehat {BCD} = 100^\circ .\)
a) Tính độ dài đường chéo AC.
b) Phần diện tích tam giác ACD sẽ được trải thảm. Tính số tiền cần chi trả cho việc trải thảm biết chi phí trải thảm cho 1 m2 là 300 000 đồng.