Bộ 5 đề thi giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mệnh đề nào dưới đây là mệnh đề sai?
Tổng hai cạnh bất kì của một tam giác lớn hơn cạnh thứ ba.
Số \(21\) không phải là số lẻ.
Số \(12\) chia hết cho \(3\).
Số \(\pi \) không phải là số hữu tỉ.
Hình vẽ nào sau đây minh họa cho tập hợp \(\left( {1;4} \right]\)?
A. ![]()
![]()
C. ![]()
![]()
Tập hợp \(N = \left\{ {x \in \mathbb{N}|x < 5} \right\}\) có bao nhiêu phần tử?
\(n\left( N \right) = 4\).
\(n\left( N \right) = 0\).
\(n\left( N \right) = 5\).
\(n\left( N \right) = 6\).
Bất phương trình nào sau đây không phải là là bất phương trình bậc nhất hai ẩn?
\[ - x + 4y > 7\].
\[2x - 4 + 3 \le 0\].
\[3x + 2 < 0\].
\[{x^2} - 3y \le 0\].
Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y + z > 10\\2x + y \le 12\end{array} \right.\).
\(\left\{ \begin{array}{l} - x + 2y \le 10\\2x + {y^2} > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \le 10\\2x + y = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \le 1\\2x + y > 10\end{array} \right.\).
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x > 0\\x + y \le 2\\x - y > 1\end{array} \right.\) chứa điểm nào sau đây?
\(B\left( {1\,;\,2} \right)\).
\(A\left( {1\,;\, - 1} \right)\).
\(C\left( {0\,;\,2} \right)\).
\[D\left( {3\,;\,1} \right)\]
Cho \(0^\circ < \alpha < 180^\circ \). Chọn khẳng định sai.
\(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\).
\[{\sin ^2}\alpha + {\cos ^2}\alpha = 1\].
\(\sin \alpha + \cos \alpha = 1\).
\(\cos \alpha + \cos \left( {180^\circ - \alpha } \right) = 0\).
Cho tam giác \(ABC\) có \(BC = a,\,\,AC = b,\,AB = c\). Gọi \(p\) là nửa chu vi, \(R\) là bán kính đường tròn ngoại tiếp, \(r\) là bán kính đường tròn nội tiếp và \(S\) là diện tích tam giác. Mệnh đề nào sau đây sai?
\(S = pr\).
\(S = \frac{1}{2}ab\sin C\).
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \).
\(S = \frac{{abc}}{{2{\rm{R}}}}\)
Cho tam giác \(ABC\) có \(AB = 4\)cm, \(BC = 7\) cm, \(AC = 9\)cm. Tính \(\cos A
\(\cos A = \frac{1}{2}\).
\(\cos A = - \frac{2}{3}\).
\(\cos A = \frac{2}{3}\).
\(\cos A = \frac{1}{3}\).
Trong các mệnh đề sau, mệnh đề nào đúng?
“\(\exists n \in \mathbb{N},n\left( {n + 1} \right)\left( {n + 2} \right)\) là số lẻ”.
“\(\forall x \in \mathbb{R},{x^2} < 4 \Leftrightarrow - 2 < x < 2\)”.
“\(\exists n \in \mathbb{N},{n^2} + 1\) chia hết cho 3”.
“\(\forall x \in \mathbb{R},{x^2} \ge 9 \Leftrightarrow x \ge \pm 3\)”.
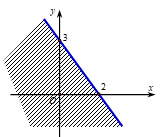
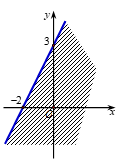
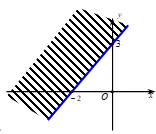
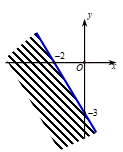
Miền nghiệm của bất phương trình \(3x - 2y > - 6\) là phần không bị gạch trong hình vẽ nào sau đây?
Giá trị của biểu thức \(A = \cos 10^\circ + \cos 20^\circ + ... + \cos 170^\circ + \cos 180^\circ \) bằng
\(A = \frac{3}{2}\).
\(A = 0\).
\(A = 1\).
\(A = - 1\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hai mệnh đề \(P\): “Tứ giác \(ABCD\) là hình vuông” và \(Q\): “Tứ giác \(ABCD\) là hình chữ nhật có hai đường chéo vuông góc với nhau”.
a) Mệnh đề đảo của mệnh đề “\(P \Rightarrow Q\)” là mệnh đề: “Nếu \(ABCD\) là hình chữ nhật có hai đường chéo vuông góc với nhau thì tứ giác \(ABCD\) là hình vuông”.
b) Hai mệnh đề \(P\) và \(Q\) không tương đương với nhau.
c) Mệnh đề \(P \Leftrightarrow Q\) là mệnh đề sai.
d)\(P\) là điều kiện cần và đủ để có \(Q\).
Cho\(\sin \alpha = \frac{1}{3}\) với \(90^\circ < \alpha < 180^\circ \).
a) Giá trị \(\sin \alpha \cdot \cos \alpha < 0\).
b) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}.\)
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}.\)
d) \[\frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \sqrt 2 \cot \alpha }} = \frac{2}{5}.\]
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho tập hợp \(A = \left\{ { - 4;\, - 2;\, - 1;\,2;\,3;\,4} \right\}\) và \(B = \left\{ {x \in \mathbb{Z}|\,\left| x \right| \le 4} \right\}\). Hỏi có bao nhiêu tập hợp \(X\) gồm bốn phần tử sao cho \(A \cup X = B\)?
Bạn Lan mang 150000 đồng đi nhà sách để mua một số quyển tập và bút. Biết rằng giá một quyển tập là 8000 đồng và giá của một cây bút là 6000 đồng. Bạn Lan có thể mua được tối đa bao nhiêu quyển tập nếu bạn đã mua 10 cây bút.
Cho tam giác\(ABC\). Tính giá trị biểu thức \(P = \sin A \cdot \cos \left( {B + C} \right) + \cos A \cdot \sin \left( {B + C} \right)\).
Cho tam giác \(ABC\) thoả mãn: \[A{C^2} + A{B^2} - B{C^2} = \sqrt 3 AC \cdot AB\]. Khi đó \(\sin \left( {B + C} \right)\) bằng bao nhiêu? (Kết quả viết dưới dạng số thập phân).
PHẦN II. TỰ LUẬN
Trong Hội khỏe phù đổng của một trường THPT, lớp 10A có 18 học sinh tham gia môn điền kinh và 14 học sinh tham gia môn bóng đá. Biết rằng trong số 40 học sinh lớp 10A có 16 học sinh không tham gia hội thi. Tìm số học sinh chỉ tham gia một môn trong hai môn trên.
Trong đợt hỗ trợ, tặng quà cho người dân vùng lũ lụt ở miền Trung, một doanh nghiệp cần thuê xe để chở ít nhất 100 người và 6 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó xe loại A có 8 chiếc và xe loại B có 6 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Nếu là chủ doanh nghiệp, em hãy đề xuất phương án để chi phí thuê xe là ít nhất?
Hai bạn Oanh, Cường lần lượt đứng tại vị trí \(O,\,C\) của một tòa nhà. Hai bạn An, Bình lần lượt đứng trên mặt đất tại vị trí mà tại đó nhìn các điểm các góc lần lượt bằng \({\alpha _1} = 30^\circ ,{\alpha _2} = 50^\circ \) và \({\beta _1} = 70^\circ ,{\beta _2} = 80^\circ \) so với phương nằm ngang. Gọi là hình chiếu của trên đường thẳng , giả sử thẳng hàng và biết khoảng cách giữa hai điểm là \(l = 20\,\,{\rm{m}}\) (Hình vẽ dưới). Gọi là khoảng cách giữa vị trí đứng của Oanh và Cường. Tìm (làm tròn kết quả đến hàng phần trăm).