Bộ 5 đề thi cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Trong các biểu thức sau, biểu thức nào là đơn thức thu gọn?
\( - {x^4}{y^3}x.\)
\(\frac{1}{3}{x^4}{y^3}.\)
\(\frac{1}{3}{x^2}{y^2}yz.\)
\(\frac{{ - 1}}{3}x{y^4}zxy.\)
Đơn thức \[30{x^2}{y^3}\] chia hết cho đơn thức nào sau đây?
\[5{x^3}{y^2}\].
\[6{y^4}\].
\[60xy\].
\[30{x^4}\].
Đẳng thức nào sau đây là hằng đẳng thức?
\(3a + 1 = a + 3\).
\(a + 3 = 3a - 1\).
\(2\left( {a - 2} \right) = 4a\).
\(a\left( {a + 1} \right) = {a^2} + a\).
Biểu thức nào sau đây không phải là phân thức đại số?
\(\frac{{x + y}}{{{x^2} - xy}}.\)
\(\frac{{2x + y}}{{8{x^3} - 1}}.\)
\(\frac{{x + 8}}{{2:x}}.\)
\(\frac{{\frac{1}{2}{x^2} - y}}{{x + 1}}.\)
Phân thức nào sau đây có tử thức là \(2x - 1\) và mẫu thức là \({x^2} - 1?\)
\(\frac{{{x^2} - 1}}{{2x - 1}}.\)
danh từ: chữ thứ tư trong mẫu tự, nốt thứ hai trong âm nhạc, sự trải ra
\(\frac{{2x - 1}}{{{x^2} + 1}}.\)
\(\frac{{2x - 1}}{{{x^2} - 1}}.\)
\(\frac{{{x^2} - 1}}{{2x + 1}}.\)
Giao điểm của đồ thị hàm số bậc nhất \(y = 3x - 6\) với trục \(Oy\) là
\(\left( {2\,;\,\,0} \right).\)
\(\left( {0\,;\,\, - 6} \right).\)
\(\left( { - 6\,;\,\,0} \right).\)
\(\left( {0\,;\,\,2} \right).\)
Cho đường thẳng \(y = ax + b.\) Với giá trị \(a\) thỏa mãn điều kiện nào sau đây thì góc tạo bởi đường thẳng đó với trục \(Ox\) là góc nhọn?
\(a < 0.\)
\(a = 0.\)
\(a > 0.\)
\(a \ne 0.\)
Tổng số cạnh bên và cạnh đáy của một hình chóp tam giác đều là
4.
6.
8.
10.
Phát biểu nào sau đây là sai?
Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là hình vuông.
Tứ giác có hai đường chéo bằng nhau là hình bình hành.
Tứ giác có 4 cạnh bằng nhau là hình thoi.
Tứ giác có 4 góc bằng nhau là hình chữ nhật.
Cho đa thức \(G = \left( {7{x^5}{y^4}{z^3} - 3{x^4}y{z^2} + 2{x^2}{y^2}z} \right):{x^2}yz\).
Đa thức \[A\] thỏa mãn \(A + 14{x^3}{y^3}{z^2} - 6{x^2}z = G\).
a) Bậc của đa thức \(G\) là 8.
b) Giá trị của biểu thức \(G\) tại \(x = 1\,;\,\,y = - 1\,;\,\,z = 1\) là 12.
c) Đa thức \[A\] có hạng tử tự do là 2.
d) Tổng của hai đa thức \[A\] và \(G\) là một đơn thức.
Cho hình bình hành \(ABCD\) có \(BC = 2AB\), \(\widehat A = 60^\circ \). Gọi \(E\), \(F\) theo thứ tự là trung điểm của \(BC\), \(AD\). Trên tia \(AB\) lấy điểm \(I\) sao cho \(B\) là trung điểm của \(AI.\)
a) \(AB = \frac{2}{3}BE\).
b) Tứ giác \(ABEF\) là hình chữ nhật.
c) Tam giác \(ADI\) cân tại \(D\).
d) \(\widehat {AED} = 90^\circ \).
Cho biểu thức \(M = {\left( {x + 3} \right)^3} - \left( {x + 9} \right)\left( {{x^2} + 27} \right)\). Giá trị của biểu thức \(M\) bằng bao nhiêu?
Cho biểu thức \[S = \left( {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} + \frac{{{x^2} - 1}}{{9 - {x^2}}}} \right):\left( {2 - \frac{{x + 5}}{{3 + x}}} \right)\,\,\,\left( {x \ne - 3\,;\,\,x \ne 3\,;\,\,x \ne - 1} \right)\].
Hỏi sau khi rút gọn biểu thức \[S\] ta được phân thức có tử thức bằng bao nhiêu?
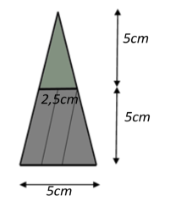
Hình ảnh bên là ảnh của một lọ nước hoa hình kim tự tháp. Khi đậy nắp, lọ có dạng hình chóp tứ giác đều (tính cả thân lọ và nắp lọ) trong đó nắp lọ cũng là hình chóp tứ giác đều có chiều cao \[5{\rm{ cm}},\] cạnh đáy \[2,5{\rm{ cm}}.\] Chiều cao thân lọ và cạnh đáy lọ đều bằng chiều cao của nắp lọ. Bỏ qua độ dày của vỏ. Tính dung tích của lọ nước hoa đó ra đơn vị mi – li – lít (làm tròn kết quả đến hàng đơn vị).
Cho tứ giác \(MNPQ\) có \(PM\) là tia phân giác của góc \(\widehat {NPQ}.\) Biết \(\widehat {QMN} = 110^\circ ,\) \(\widehat {N\,} = 120^\circ \) và \(\widehat {Q\,} = 60^\circ .\) Tính số đo của \(\widehat {MPQ}\) (đơn vị: độ).
(1,5 điểm) Một công ty viễn thông A cung cấp dịch vụ truyền hình cáp với mức phí ban đầu là 300 000 đồng và mỗi tháng phải đóng 150 000 đồng. Công ty viễn thông B cũng cung cấp dịch vụ truyền hình cáp nhưng không tính phí ban đầu và mỗi tháng khách hàng sẽ phải đóng 200 000 đồng.

a) Gọi \[T\] (đồng) là số tiền khách hàng phải trả cho mỗi công ty viễn thông trong \[t\] (tháng) sử dụng dịch vụ truyền hình cáp. Khi đó hãy lập hàm số \[T\] theo t đối với mỗi công ty.
b) Tính số tiền khách hàng phải trả sau khi sử dụng dịch vụ truyền hình cáp trong 5 tháng đối với mỗi công ty.
c) Khách hàng cần sử dụng dịch vụ truyền hình cáp trên mấy tháng thì đăng kí bên công ty viễn thông A sẽ tiết kiệm chi phí hơn?
(1,0 điểm) Cho hình vuông \[ABCD.\] Lấy điểm \[M\] thuộc đường chéo \[BD.\] Kẻ \[ME\] vuông góc với \(AB\) tại \[E,{\rm{ }}MF\] vuông góc với \[AD\] tại \[F.\]
a) Tứ giác \(AEMF\) là hình gì? Vì sao?
b) Xác định vị trí của điểm \[M\] trên đường chéo \[BD\] để diện tích của tứ giác \[AEMF\] lớn nhất.
(0,5 điểm) Tìm \(a,\,\,b,\,\,c \in \mathbb{N}*\) sao cho \(\left( {a - \frac{1}{b}} \right)\left( {b - \frac{1}{c}} \right)\left( {c - \frac{1}{a}} \right) \in \mathbb{N}*\).
(0,5 {c - \ frac {1} {a}} \ right) \ in \ mathbb {n}*\).
Biểu thức nào sau đây có thể là nhân tử chung khi phân tích đa thức \[5{x^2}\left( {2x - 5} \right) - 4x + 10\] thành nhân tử?
\(2x - 5.\)
\(5 + 2x.\)
\(4x - 10.\)
\(4x + 10.\)
Diện tích xung quanh của hình chóp đều bằng
Tích nửa chu vi đáy và đường cao của hình chóp.
Tổng chu vi đáy và trung đoạn.
Tích chu vi đáy và trung đoạn.
Tích nửa chu vi đáy và trung đoạn.
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau?
\(15\;\;{\rm{cm}};\,\,8\;\;{\rm{cm;}}\,\,{\rm{18}}\;\;{\rm{cm}}\,{\rm{.}}\)
\(2\;\;{\rm{cm}};\,\,3\;\;{\rm{cm;}}\,\,4\;\;{\rm{cm}}\,{\rm{.}}\)
\(5\;\;{\rm{m}};\,\,6\;\;{\rm{m;}}\,\,{\rm{8}}\;\;{\rm{m}}\,{\rm{.}}\)
\[21\;\;{\rm{dm}};\,\,20\;\;{\rm{dm;}}\,\,29\;\;{\rm{dm}}\,{\rm{.}}\]








