Bộ 5 đề thi cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 1
21 câu hỏi
Đa thức \(A = {x^2} + 2{y^5} - {x^4}{y^4} - 1\) có bao nhiêu hạng tử?
3.
4.
5.
6.
Hai đơn thức thu gọn trong các đơn thức đã cho là
\(A\) và \(B.\)
\(B\) và \(C.\)
\(A\) và \(D.\)
\(A\) và \(C.\)
Khẳng định nào sau đây là sai?
Hướng dẫn giải
\({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\).
\({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\).
\({x^3} - {y^3} = \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\).
\({\left( {x - y} \right)^3} = {x^3} - {y^3}\).
Biểu thức nào sau đây không phải là phân thức?
\(\frac{{5xy - 7}}{{{y^2}}}.\)
\(5x{y^2} - 2.\)
\(\frac{{{x^2} - 2x + 4}}{{3x - 1}}.\)
\(\frac{{2{x^2} - x + 1}}{{\frac{1}{{x - y}}}}.\)
Đa thức nào sau đây không là mẫu thức chung của hai phân thức \(\frac{1}{x};\,\,\frac{1}{{{y^2}}}?\)
\(\left( {{x^2} + x} \right){y^2}.\)
\(2{x^3}{y^2}.\)
\(x\left( {x + 1} \right)y.\)
\(2x{y^2}{\left( {y - 1} \right)^2}.\)
Đồ thị hàm số \(y = ax{\rm{ }}\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua
gốc tọa độ \(O\left( {0\,;\,\,0} \right).\)
điểm \(A\left( {1\,;\,\,0} \right).\)
điểm \(B\left( {0\,;\,\,1} \right).\)
điểm \(C\left( {1\,;\,\,1} \right).\)
Biết rằng đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song, khi đó hệ số \(a\) bằng
\(1.\)
\(2.\)
\(3.\)
\(0.\)
Một hình chóp tứ giác đều có cạnh đáy là \(a\) và độ dài đường cao là \(b\) thì có thể tích là
A. \(V = \frac{1}{3}{a^2}b.\)
B. \(V = {a^2}b.\)
C. \(V = 3{a^2}b.\)
D. \(V = \frac{1}{2}{a^2}b.\)
Cho các hình vẽ sau:
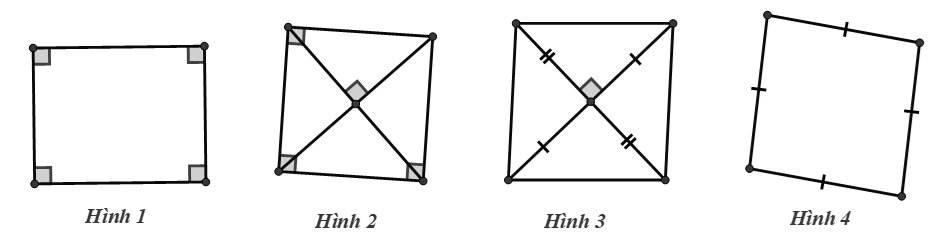
Trong các hình sau, những hình nào là hình vuông?
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Cho hai đa thức:
\(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\) và \[B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}.\]
Đa thức \(M\) thỏa mãn \(A = M + B.\)
a) Bậc của đa thức \[A\] là 8.
b) Hệ số tự do của đa thức \(B\) là 2.
c) Giá trị của biểu thức \(B\) tại \[x = - 1\,;\,\,y = 1\] là 12.
d) \(M\)là một đơn thức.
Cho tam giác \[ABC\]. Dựng bên ngoài tam giác đó hai tam giác \[ABD,{\rm{ }}ACE\] vuông cân tại đỉnh \[A\] rồi dựng hình bình hành \[AEID\]. Biết \[\widehat {DAI} = \widehat {ABC}\]. Gọi \[K\] là trung điểm của \[BD.\]
a) \[\widehat {DAI} + \widehat {BAH} = 45^\circ \].b) \[AI \bot BC\].
c) \(\widehat {EBA} = \widehat {CDA}\).d) \[KA = \frac{1}{2}KB\].
Tìm giá trị của \[a\] để biểu thức \[4{x^2} - 20x + 5a\] là bình phương của một hiệu.
Cho biểu thức \[U = \frac{{5x + 1}}{{2x - 3}} \cdot \frac{{x + 2}}{{25{x^2} - 1}} - \frac{{8 - 3x}}{{25{x^2} - 1}}:\frac{{2x - 3}}{{5x + 1}}\,\,\,\left( {x \ne \frac{3}{2}\,;\,\,x \ne \frac{1}{5}\,;\,\,x \ne - \frac{1}{5}} \right)\].
Hỏi sau khi rút gọn biểu thức \[U\] ta được phân thức có tử thức bằng bao nhiêu?
Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\)
Tứ giác \[ABCD\] có số đo các góc \[\widehat A\,,\,\,\widehat B\,,\,\,\widehat C\,,\,\,\widehat D\] tỉ lệ thuận với \[4\,;\,\,3\,;\,\,5\,;\,\,6.\] Tính số đo \[\widehat {A\,\,}\] theo đơn vị độ.
(1,5 điểm) Một cửa hàng sách cũ có một chính sách như sau: nếu khách hàng đăng kí làm hội viên của cửa hàng sách thì mỗi năm phải đóng \[50\,\,000\] đồng chi phí và chỉ phải mướn sách với giá \[5\,\,000\] đồng/cuốn sách, còn nếu khách hàng không phải hội viên thì sẽ mướn sách với giá \[10\,\,000\] đồng/cuốn sách. Gọi \[s\] (đồng) là tổng số tiền mỗi khách hàng phải trả trong mỗi năm và \[t\] là số cuốn sách mà khách hàng mướn.
![(1,5 điểm) Một cửa hàng sách cũ có một chính sách như sau: nếu khách hàng đăng kí làm hội viên của cửa hàng sách thì mỗi năm phải đóng \[50\,\,000\] đồng chi phí và chỉ phải mướn sách với giá (ảnh 1)](https://video.vietjack.com/upload2/images/1752729593/1752729655-image5.jpeg)
a) Lập hàm số của
\[s\] theo \[t\] đối với khách hàng là hội viên và với khách hàng không phải là hội viên.
b) Trung là một hội viên của cửa hàng sách, năm ngoái thì Trung đã trả cho cửa hàng sách tổng cộng \[90\,\,000\] đồng. Hỏi nếu Trung không phải là hội viên của cửa hàng sách thì số tiền phải trả là bao nhiêu?
c) Một hội viên cần thuê tối thiểu bao nhiêu cuốn sách để có thể bù được phí hội viên?
(1,0 điểm) Cho tam giác \[ABC\] có các đường trung tuyến \[BD,{\rm{ }}CE\] cắt nhau tại \[G.\] Gọi \[F,{\rm{ }}H\] lần lượt là trung điểm của \[BG,{\rm{ }}CG.\]
a) Tứ giác \[EFHD\] là hình gì? Vì sao?
b) Tìm điều kiện của tam giác \[ABC\] để tứ giác \[EFHD\] là hình vuông.
(0,5 điểm) Tính giá trị lớn nhất của biểu thức \(A = \frac{{2 + 2x - {x^2}}}{{{x^2} - 2x + 3}}\).
Số đo mỗi góc ở đỉnh của đáy hình chóp tam giác đều là
\(180^\circ .\)
\(120^\circ .\)
\(90^\circ .\)
\(60^\circ .\)
Gấp mảnh giấy hình chữ nhật như hình vẽ sau đây sao cho điểm \(D\) trùng với điểm \(E\), là một điểm nằm trên cạnh \(BC.\) Biết rằng \(AD = 10{\rm{ cm, }}\,AB = 8{\rm{ cm}}{\rm{.}}\) Hỏi độ dài của cạnh \(EC\) bằng bao nhiêu?
![Câu 11. Gấp mảnh giấy hình chữ nhật như hình vẽ sau đây sao cho điểm \(D\) trùng với điểm \(E\), là một điểm nằm trên cạnh \(BC.\) Biết rằng \(AD = 10{\rm{ cm, }}\,AB = 8{\rm{ cm}}{\rm{.}}\) Hỏi độ dài của cạnh \(EC\) bằng bao nhiêu? C. A. \[3{\rm{ cm}}.\] D. B. \[4{\rm{ cm}}.\] A. C. \[6{\rm{ cm}}.\] B. D. \[8{\rm{ cm}}.\] (ảnh 1)](https://video.vietjack.com/upload2/images/1752729593/1752729655-image1.png)
\[3{\rm{ cm}}.\]
\[4{\rm{ cm}}.\]
\[6{\rm{ cm}}.\]
\[8{\rm{ cm}}.\]
Với mọi giá trị \(x \in \mathbb{R}\) thì giá trị của biểu thức \({x^2} - 20x + 101\) là một số
dương.
không âm.
không dương.
âm.








