Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án - Đề 8
16 câu hỏi
Bậc của đa thức \({x^2}{y^5} - {x^2}{y^4} + {y^6} + 1\) là
\[4\];
\(5\);
\(6\);
\(7\).
Cặp đơn thức nào sau đây không đồng dạng?
\(7{x^3}y\) và \(\frac{1}{{15}}{x^3}y\);
\( - \frac{1}{8}{\left( {xy} \right)^2}{x^2}\) và \(32{x^2}{y^3}\);
\(5{x^2}{y^2}\) và \( - 2{x^2}{y^2}\);
\(a{x^2}y\) và \(2b{x^2}y\) \((a,b\) là các hằng số khác \(0).\)
Giá trị của biểu thức \(A = {x^4} + 4{x^2}y - 6z\) tại \(x = 4,y = - 5,z = - 2\) là
\( - 76\);
\( - 52\);
\( - 25\);
\(37\).
Cho \({x^3} + 12{x^2} + 48x + 64 = {\left( {x + a} \right)^3}\). Giá trị của \(a\) là
\( - 64\);
64;
\( - 4\);
4.
Quy đồng mẫu thức hai phân thức \(\frac{2}{{{x^2}y}}\) và \(\frac{3}{{x{y^2}}}\) ta được mẫu thức chung là
\({x^2}y\);
\(x{y^2}\);
\({x^2}{y^2}\);
\({x^3}{y^3}\).
Phân thức \(\frac{{x - 1}}{{x + 1}}\) là kết quả của phép tính nào dưới đây?
\(\frac{x}{{x + 1}} - \frac{2}{{x + 1}}\);
\(\frac{{2x}}{{x + 1}} - \frac{2}{{x + 1}}\);
\[\frac{{ - x}}{{x + 1}} - \frac{1}{{x + 1}}\];
\(\frac{x}{{x + 1}} - \frac{{ - 1}}{{ - \left( {x + 1} \right)}}\).
Hình chóp nào sau đây là hình chóp tam giác đều?
Hình có đáy là tam giác;
Hình có đáy là tam giác đều;
Hình có đáy là tam giác đều và tất cả các cạnh đều vuông góc với mặt đáy;
Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.
Một hình chóp tứ giác đều có diện tích xung quanh \({S_{xq}}\) và chiều cao \(h\). Khi đó nửa chu vi đáy là
\(\frac{{2{S_{xq}}}}{h}\);
\(\frac{{{S_{xq}}}}{h}\);
\(\frac{{{S_{xq}}}}{{2h}}\);
\(\frac{{2h}}{{{S_{xq}}}}\).
Thu gọn biểu thức:
a) \(\frac{{27}}{{15}}{x^3}y{z^5}:\frac{9}{5}x{z^2};\)
b) \(3x\left( {x - y} \right) - y\left( {y - 3x} \right)\);
c) \(\left( {x - y} \right)\left( {{x^2} + {y^2}} \right) - \left( {{x^4}y - x{y^4}} \right):xy\).
Phân tích đa thức thành nhân tử:
a) \(2{x^3} - 6{x^2}\); b) \(9{x^2} - \frac{1}{{16}}{y^2}\); c) \({x^2}y + 5x{y^2} + 6{y^3}\).
Cho biểu thức \(A = \frac{{x - 2}}{{x + 2}}\).
a) Tìm điều kiện xác định của biểu thức \(A.\)
b) Tìm biểu thức \(C\) sao cho \(C = A - B\) với \(B = \frac{x}{{x - 2}} + \frac{{9x + 2}}{{4 - {x^2}}}\) \(\left( {x \ne \pm 2} \right).\)
Một khối bê tông có dạng như hình vẽ bên. Phần đáy của bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh 40 cm, chiều cao 25 cm. Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao 100 cm. Tính thể tích của khối bê tông đó (làm tròn kết quả đến hàng đơn vị). 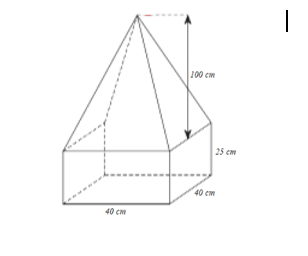
Cho tứ giác \(ABCD,\) trong đó có \(\widehat {A\,\,} + \widehat {B\,} = 140^\circ \). Tính tổng số đo góc ngoài tại đỉnh \(C\) và \(D\) của tứ giác.
Khi xây móng nhà, để kiểm tra xem 2 phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\] cm, \[AC = 4\] cm \[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\] cm thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?
Chứng minh rằng với mọi \(a,b,c\) ta luôn có:
\({\left( {a + b + c} \right)^3} = {a^3} + {b^3} + {c^3} + 3\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right).\)
Đơn thức \(\left( { - \frac{1}{5}{x^2}{y^3}} \right)\left( { - 5{x^3}y} \right)ax\) \((a\) là hằng số) có hệ số và bậc lần lượt là
\(a\) và \(6\);
\(1\) và 10;
\(a\) và 10;
1 và 6.








