Bộ 5 đề thi cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 4
21 câu hỏi
Cho các biểu thức: \[{x^2} + {y^2};\] \[2\,\,025;\] \[\frac{3}{x} + y;\] \[\frac{x}{y} + \frac{1}{5}x;\] \[\frac{x}{2} + xyz;\] \[4 + x\sqrt {yz} \] có bao nhiêu đa thức?
1.
2.
3.
4.
Đơn thức \[6{x^4}{y^3}\] chia hết cho đơn thức nào sau đây?
\[6{x^4}{y^3}z\].
danh từ: nốt si
\[4{x^5}y\].
\[2{x^3}\].
\[3{x^4}{y^4}\].
Khẳng định nào sau đây đúng?
\({\left( { - x - 3} \right)^2} = {\left( {x + 3} \right)^2}.\)
\({\left( {x - 2} \right)^2} = {x^2} - 4.\)
\({\left( {y - 2} \right)^3} = {\left( {2 - y} \right)^3}.\)
\({\left( {x - 3} \right)^2} = - {\left( {3 - x} \right)^2}.\)
Cho hai phân thức có mẫu thức là \(2{x^3}{y^2}\left( {y - 1} \right)\) và \({x^2}{y^3}{\left( {y - 1} \right)^2}.\) Mẫu thức chung của hai phân thức đó là
\(2{x^3}{y^3}\left( {y - 1} \right).\)
\(2{x^3}{y^3}{\left( {y - 1} \right)^2}.\)
\({x^3}{y^3}{\left( {y - 1} \right)^2}.\)
\(2{x^2}{y^3}{\left( {y - 1} \right)^2}.\)
Cho hàm số \(y = f\left( x \right) = 2{x^2} - 1.\) Khẳng định nào sau đây là đúng?
\(f\left( { - 1} \right) = - 3.\)
\(f\left( 1 \right) = 1.\)
\(f\left( { - 1} \right) = - 1.\)
\(f\left( 1 \right) = 3.\)
Giá trị của \(m\) để đồ thị hàm số \(y = \left( {m + 2} \right)x + 5\) là đường thẳng có hệ số góc bằng \( - 3\) là
\(m = 5.\)
\(m = 3.\)
\(m = - 3.\)
\(m = - 5.\)
Nhận định nào sau đây là đúng?
Nếu hình chóp có đáy là hình thoi, chân đường cao trùng với tâm hình thoi thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình chữ nhật, chân đường cao trùng với giao điểm của hai đường chéo đáy thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình vuông thì nó là hình chóp đều.
Nếu hình chóp có đáy là tam giác đều, chân đường cao trùng với trọng tâm của tam giác thì nó là hình chóp đều.
Một hình chóp đều và một hình lăng trụ đứng có diện tích đáy bằng nhau. Chiều cao của hình chóp đều gấp đôi chiều cao của hình lăng trụ đứng. Thể tích của hình chóp đều là
\(V = \frac{1}{3}Sh.\)
\[V = Sh.\]
\(V = \frac{2}{3}Sh.\)
\(V = 2Sh.\)
Nhà bạn An (vị trí \[A\] trên hình vẽ) cách nhà bạn Châu (vị trí \[C\] trên hình vẽ) \[600\,\,{\rm{m}}\]và cách nhà bạn Bình (vị trí \[B\] trên hình vẽ) \[450\,\,{\rm{m}}.\] Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là ba đỉnh của một tam giác vuông (như hình vẽ). Tính khoảng cách từ nhà Bình đến nhà Châu.
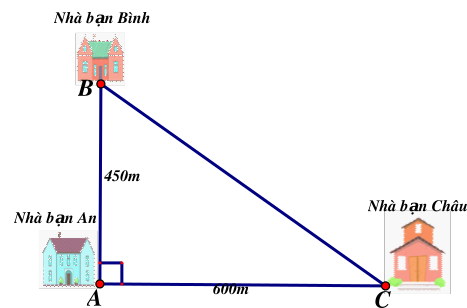
\[396{\rm{ m}}\].
\[750{\rm{ m}}\].
\[150{\rm{ m}}\].
\[250{\rm{ m}}\].
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(D,\,\,E\) theo thứ tự thuộc các cạnh bên \(AB,\,\,AC\) sao cho \(DE\,{\rm{//}}\,BC\). Tứ giác \(BDEC\) là hình gì?
Hình thang cân.
Hình thang vuông.
Hình bình hành.
Hình thoi.
Cho hai đa thức:
\(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\) và \[B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}.\]
Đa thức \(M\) thỏa mãn \(A = M + B.\)
a) Bậc của đa thức \[A\] là 8.
b) Hệ số tự do của đa thức \(B\) là 2.
c) Giá trị của biểu thức \(B\) tại \[x = - 1\,;\,\,y = 1\] là 12.
d) \(M\)là một đơn thức.
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\,,\) đường cao \(AH\,.\) Từ \(H\) kẻ \(HM \bot AB\,\,\left( {M \in AB} \right)\,.\) Kẻ \(HN \bot AC\,\,\left( {N \in AC} \right)\,.\) Trên tia đối của tia \[MH\] lấy điểm \[P\] sao cho \[M\] là trung điểm của \[PH.\] Gọi \(I\) là trung điểm của \(HC\,,\) lấy \(K\) trên tia \(AI\) sao cho \(I\) là trung điểm của \(AK;\,\,MN\) cắt \(AH\) tại \(O,\) \(CO\) cắt \(AK\) tại \(D.\)
a) \(\widehat {HKC} = \frac{1}{2}\widehat {HAC}\).
b) Tứ giác \[AMHN\] là hình chữ nhật.
c) Tứ giác \(MNCK\) là hình thang vuông.
d) \(AK = 2AD\).
Cho biểu thức \(V = {\left( {2x - 1} \right)^3} - 2\left( {x - 2} \right)\left( {4{x^2} + 2x + 7} \right) - 15\). Giá trị của biểu thức \(V\) bằng bao nhiêu?
Cho biểu thức \(D = \left( {\frac{{x + 2}}{{3x}} + \frac{2}{{x + 1}} - 3} \right):\frac{{2 - 4x}}{{x + 1}} - \frac{{3x - {x^2} + 1}}{{3x}}\,\,\left( {x \ne 0\,;\,\,x \ne - 1\,;\,\,x \ne \frac{1}{2}} \right)\).
Hỏi sau khi rút gọn biểu thức \(D\) ta được phân thức có mẫu thức bằng bao nhiêu?
Người ta thiết kế một chậu cây có dạng chóp tam giác đều có cạnh đáy \[4{\rm{ cm}}\]và trung đoạn hình chóp là \[6{\rm{ cm}}{\rm{.}}\] Tính diện tích miếng bìa cần để bọc xung quanh một chậu cây theo đơn vị \({\rm{c}}{{\rm{m}}^{\rm{2}}}\) (không tính đến phần đường viền, nếp gấp).
Cho tứ giác \(ABCD\) có \(\widehat C = 60^\circ \,;\,\,\widehat D = 80^\circ \,;\,\,\widehat A - \widehat B = 10^\circ .\) Tính \(\widehat A + 2\widehat B\) theo đơn vị độ.
(1,5 điểm) Giá trị sổ sách là giá trị của tài sản mà một công ty sử dụng để tạo ra bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm đi một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt vào tài sản. Giả sử rằng một công ty vận tải vừa mua một số ô tô mới với giá là 640 triệu đồng một chiếc. Công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe sẽ giảm giá \[640:8 = 80\] (triệu đồng).

a) Tìm hàm số bậc nhất biểu thị giá trị sổ sách \[V\] (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi \[x\] (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất tìm được ở câu a.
c) Khi nào giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng?
(1,0 điểm) Cho hình vuông \(ABCD\). Lấy \(E\) là điểm trên cạnh \(DC\,;\,\,F\) là điểm trên tia đối của tia \(BC\) sao cho \(BF = DE\). Gọi \(I\) là trung điểm của \(EF.\)
a) Chứng minh tam giác \(AEF\)vuông cân.
b) Lấy điểm \(K\) đối xứng với \(A\) qua \(I.\) Tứ giác \(AEKF\) là hình gì?
(0,5 điểm) Cho ba số thực \(a,\,\,b,\,\,c\) khác \(2\) và thỏa mãn \(a + b + c = 6.\) Tính giá trị của biểu thức:
\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}.\)
Phân tích đa thức \({x^5} - {x^3} - {x^2} + 1\) thành nhân tử ta được
\[{\left( {x + 1} \right)^2}\left( {x - 1} \right)\left( {{x^2} + x + 1} \right).\]
\[{\left( {x + 1} \right)^2}\left( {x - 1} \right)\left( {{x^2} - x + 1} \right).\]
\[{\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + x + 1} \right).\]
\[{\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} - x + 1} \right).\]
Với điều kiện các phân thức có nghĩa. Phân thức \(\frac{{ - 2xy}}{{6{x^3}{y^2}}}\) bằng phân thức nào sau đây?
\(\frac{{ - 1}}{{3x{y^2}}}.\)
\(\frac{{ - 1}}{{3{x^2}y}}.\)
\(\frac{{ - 0}}{{{x^2}y}}.\)
\(\frac{{ - 1}}{{2{x^2}y}}.\)








