Bộ 5 đề thi cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 3
21 câu hỏi
Cho các biểu thức đại số sau:
\( - 6{x^2}y;\,\,\,{x^3} - \frac{1}{2}xy;\,\,\,5{z^3};\,\,\, - \frac{4}{7}y{z^2}.5;\,\,\,\, - 3x + 7y;\,\,\,\,\left( {\sqrt 2 - 1} \right)x;\,\,\,\,x\sqrt y \).
Có bao nhiêu đơn thức trong các biểu thức đã cho ở trên?
5.
4.
3.
2.
Cho các đơn thức \(A = \left( {0,3 + \pi } \right){x^2}y;\) \(B = \frac{1}{2}xy{x^2}z;\) \(C = - xyx{z^2}\) và \(D = \left( {\sqrt 2 + 1} \right)x{y^2}z.\) Hai đơn thức thu gọn trong các đơn thức đã cho là
\(A\) và \(B.\)
\(B\) và \(C.\)
\(A\) và \(D.\)
\(A\) và \(C.\)
Khẳng định nào sau đây là đúng?
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\).
\({\left( {A + B} \right)^2} = {A^2} + AB + {B^2}\).
\({\left( {A + B} \right)^2} = {A^2} + {B^2}\).
\({\left( {A + B} \right)^2} = {A^2} - 2AB + {B^2}\).
Phân thức nào sau đây là phân thức đối của phân thức \(\frac{{2 - x}}{{3x}}?\)
\(\frac{{2 + x}}{{3x}}.\)
\(\frac{{x - 2}}{{3x}}.\)
\(\frac{{3x}}{{2 - x}}.\)
\(\frac{{3x}}{{x - 2}}.\)
Hàm số nào sau đây là hàm số bậc nhất?
\(y = 0x + 3.\)
\(y = 2{x^2} + 1.\)
\(y = - x.\)
\(y = 0.\)
Điểm \(M\) trên mặt phẳng tọa độ \[Oxy\] (hình bên) có tọa độ là

\(\left( { - 1\,;\,\,1} \right).\)
\(\left( { - 2\,;\,\,1} \right).\)
\(\left( {1\,;\,\, - 1} \right).\)
\(\left( {1\,;\,\, - 2} \right).\)
Khẳng định nào sau đây là đúng?
Hình chóp tam giác đều có 3 mặt.
Hình chóp tứ giác đều có 4 đỉnh.
Hình chóp tứ giác đều có đáy là hình thoi.
Hình chóp tam giác đều có 6 cạnh.
Một hình chóp tứ giác đều có cạnh đáy là \(a\) và độ dài trung đoạn là \(b\) thì có diện tích xung quanh là
\({S_{xq}} = 2ab.\)
\({S_{xq}} = ab.\)
\({S_{xq}} = \frac{1}{2}ab.\)
\({S_{xq}} = 4ab.\)
Hình bình hành \[ABCD\;\] là hình chữ nhật khi
\[AB = AD.\]
\(\widehat A = 90^\circ .\)
\[AB = 2AC\].
\(\widehat A = \widehat C.\)
Cho hai đa thức:
\[R = \left( {xy - 4{x^2} + 2} \right) \cdot x{y^2}\] và \[T = \left( {15{x^3}{y^4} - 20{x^4}{y^3} + 10{x^2}{y^3}} \right):5xy.\]
Đa thức \(S\) thỏa mãn \(R = T - S.\)
a) Hệ số tự do của đa thức \(R\) là 2.
b) Bậc của đa thức \(T\) là 3.
c) Giá trị của biểu thức \(T\) tại \[x = 1\,;\,\,y = - 1\] là \( - 5\).
d) \(S\) là một đơn thức.
Cho tam giác nhọn \[ABC\] có \[AB < BC.\] Từ trung điểm \(M\) của cạnh \(AB\) kẻ đường thẳng song song với \(BC\) cắt cạnh \(AC\) tại \(N.\) Trên cạnh \(BC\) lấy điểm \(D\) sao cho \(BD = MN.\) Kẻ đường cao \[AH\left( {H \in BC} \right)\] của tam giác \[ABC\].
a) Tứ giác \(BMND\)là hình bình hành.
b) Tam giác \(AMH\) cân tại \(A\).
c) \(\widehat {AMN} = \frac{2}{3}\widehat {HMN}.\)
d) Tứ giác \(DHMN\) là hình thang cân.
Có bao nhiêu giá trị của \(x\) thỏa mãn \({x^3}--2{x^2} + x = 0?\)
Cho biểu thức \[K = \frac{{{x^3} - 1}}{{{x^2} - 4}} \cdot \left( {\frac{1}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}} \right)\,\,\,\left( {x \ne - 2\,;\,\,x \ne 2\,;\,\,x \ne 1} \right)\]. Hỏi sau khi rút gọn biểu thức \[K\] ta được phân thức có tử thức bằng bao nhiêu?
Một khối rubik có dạng hình chóp tam giác đều (các mặt khối rubic là các tam giác đều bằng nhau), có chu vi đáy bằng \[180{\rm{ mm}},\] đường cao của mặt bên hình chóp là \[67\,\,{\rm{mm}}.\] Tính diện tích toàn phần (tổng diện tích các mặt) của khối rubik đó.

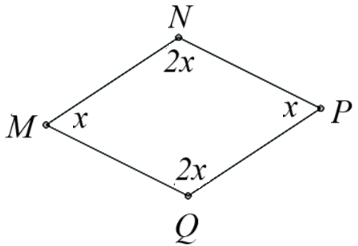
Tìm \(x\) trong hình vẽ dưới đây theo đơn vị độ.
(1,5 điểm) Giả sử rằng lượng cung \[S\] và lượng cầu \[D\] về áo phông tại một buổi biểu diễn được cho bởi các hàm số sau:
\[S\left( p \right) = -600 + 10p;{\rm{ }}\,\,\,D\left( p \right) = 1{\rm{ }}200-20p,\]
trong đó \[p\] (nghìn đồng) là giá của một chiếc áo phông.
a) Tìm mức giá cân bằng (tức là mức giá mà lượng cung bằng lượng cầu) của áo phông tại buổi biểu diễn này.
b) Vẽ đồ thị của hai hàm số \[S\left( p \right)\] và \[D\left( p \right)\] trên cùng một hệ trục tọa độ.
c) Từ kết quả câu b, xác định mức giá của áo phông mà lượng cung lớn hơn lượng cầu. Khi đó, điều gì sẽ xảy ra?
(1,0 điểm) Cho tam giác \[ABC\] vuông cân tại \(A.\) Lấy điểm \[M\] thuộc cạnh huyền \[BC.\] Gọi \[D,{\rm{ }}E\] lần lượt là hình chiếu của điểm \[M\] trên đường thẳng \[AB,{\rm{ }}AC.\]
a) Tứ giác \[ADME\] là hình gì? Vì sao?
b) Chứng minh khi điểm \[M\] thay đổi vị trí trên cạnh \[BC\] thì chu vi của tứ giác \[ADME\] không đổi.
(0,5 điểm) Cho phân thức \(A = \frac{{{x^4} + {x^3} + x + 1}}{{{x^4} - {x^3} + 2{x^2} - x + 1}}.\) Chứng minh rằng \(A\) luôn không với mọi giá trị thực của \(x.\)
Phân tích đa thức \[3{x^2} - 6xy + 3{y^2} - 12{z^2}\] thành nhân tử ta được
\(3\left( {x - y - 2z} \right)\left( {x + y + 2z} \right)\).
\(\left( {x + y - 2z} \right)\left( {x - y + 2z} \right)\).
\(3\left( {x + y - 2z} \right)\left( {x + y + 2z} \right)\).
\(\left( {x + y - 2z} \right)\left( {x + y + 2z} \right)\).
Biểu thức nào sau đây có dạng phân thức?
\(\frac{x}{0}.\)
\(\frac{{x + y}}{{\frac{1}{y}}}.\)
\(\frac{{{x^2} + y}}{{\frac{1}{2}y}}.\)
\(\frac{1}{{\frac{{{x^2} - {y^2}}}{{xy}}}}.\)
Cho tam giác \(ABC\) có đường cao \(AH.\) Biết \(AC = 15\;\;{\rm{cm}},\,\,AH = 12\;\;{\rm{cm,}}\,\,BH = 9\;\;{\rm{cm}}.\) Hỏi tam giác \(ABC\) là tam giác gì?
Tam giác cân.
Tam giác vuông.
Tam giác cân.
Tam giác tù.








