Bộ 5 đề thi cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 2
21 câu hỏi
Kết quả của phép cộng hai đơn thức \(2x{y^2}z\) và \( - {x^2}yz\) là
Một đơn thức.
Một đa thức nhưng không phải đơn thức.
Một số.
Không xác định.
Bậc của đa thức \(A = {x^6} + {y^5} + {x^4}{y^4} + 1\) là
4.
danh từ: nốt si
5.
6.
8.
Đẳng thức nào sau đây là hằng đẳng thức?
\[4{a^2} - 1 = 3a\].
\[\left( {a + 2} \right)\left( {a - 2} \right) = {a^2} - 4\].
\[5a\; = 3a + 1\].
\[{a^2} - 1 = 2a + 1\].
Khẳng định nào sau đây là đúng?
\(\frac{A}{B} = \frac{{ - A}}{{ - B}}.\)
\(\frac{A}{B} = \frac{A}{{ - B}}.\)
\(\frac{A}{B} = \frac{{ - A}}{B}.\)
\(\frac{A}{B} = - \frac{{ - A}}{{ - B}}.\)
Phân thức nghịch đảo của phân thức \( - \frac{{3{y^2}}}{{2x}}\) là
\(\frac{{3{y^2}}}{{2x}}.\)
\( - \frac{{2{x^2}}}{{3y}}.\)
\( - \frac{{2x}}{{3{y^2}}}.\)
\(\frac{{2x}}{{3{y^2}}}.\)
Hàm số nào sau đây là hàm số bậc nhất?
\(y = 2x - 1.\)
\(y = 2.\)
\[y = {x^2} + x + 1.\]
\(y = \frac{2}{x}.\)
Đồ thị hàm số \(y = x + 2\) đi qua điểm có tọa độ nào sau đây?
\(\left( {0\,;\,\, - 2} \right).\)
\(\left( {1\,;\,\,3} \right).\)
\(\left( { - 1\,;\,\,0} \right).\)
\(\left( {0\,;\,\,0} \right).\)
Cho hình chóp tam giác đều \(A.BCD\) như hình vẽ bên. Đoạn thẳng nào sau đây là trung đoạn của hình chóp?
\(AC\).
\(AM\).
\(BN\).
\(AP\).
Một công ty muốn làm một đường ống dẫn từ nhà máy \(C\) trên bờ đến một điểm \({\rm{B}}\) trên đất liền. Điểm \(A\) đảo cách bờ biển ở điểm \(B\) là \(9\,\;{\rm{km}}.\) Giá để xây dựng đường ống từ nhà máy trên biển điểm \(B\) đến diểm \(C\) trên bờ là \(5\,\,000\,\,{\rm{USD}}/{\rm{km}}.\) Khoảng cách từ \(A\) đến \(C\) là \(12\;\,{\rm{km}}{\rm{.}}\) Biết \(1\,\,{\rm{USD}} = 26\,\,115\) đồng tại thời điểm đó. Hỏi chi phí làm đường ống từ điểm \(B\) tới điểm \(C\) của công ty trên khoảng bao nhiêu tỉ đồng? (làm tròn đến chữ số thập phân thứ ba)
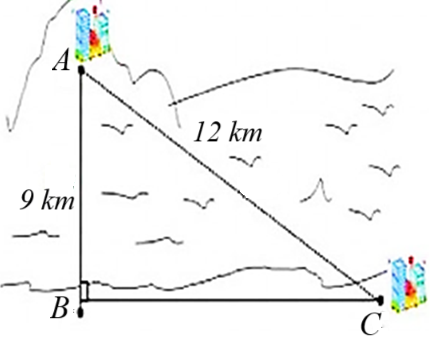
\(1,121\) tỉ đồng.
\(1,036\) tỉ đồng.
\(1,306\) tỉ đồng.
\(1,959\) tỉ đồng.
Cho đa thức \(U = \left( {10{x^5}{y^3} - 25{x^3}{y^2} + 20{x^4}{y^3}} \right):\left( { - 5{x^2}{y^2}} \right)\) và \(V = 2{x^2}y\left( {x + 2} \right)\).
a) Hệ số cao nhất của của đa thức \(U\) là 5.
b) Giá trị của biểu thức \(U\) tại \(x = - 1\,;\,\,y = 2\) là 10.
c) Bậc của đa thức \(V\) là 4.
d) Tổng của hai đa thức \(U\) và \(V\) chia hết cho 5.
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\) là một điểm bất kì trên cạnh huyền \(BC\). Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(M\) xuống \(AB\) và \(AC.\) Lấy điểm \(I\) sao cho \(A\) là trung điểm của \(ID\); điểm \(K\) sao cho \(M\) là trung điểm của \(EK\).
a) \(IA = ID\,;\,\,KM = KE.\)
b) Tứ giác \(ADME\) là hình chữ nhật.
c) Tứ giác \(ADMC\) là hình thang cân.
d) \(DK\,{\rm{//}}\,EI\).
Cho biểu thức \[T = \left( {{x^2} - 6x + 12} \right)\left( {x - 6} \right) - {\left( {x - 4} \right)^3}\]. Giá trị của biểu thức \[T\] bằng bao nhiêu?
Cho biểu thức \[I = \frac{{{{\left( {x + 2} \right)}^2}}}{x} \cdot \left( {1 - \frac{{{x^2}}}{{x + 2}}} \right) - \frac{{{x^2} + 6x + 4}}{x}\,\,\,\left( {x \ne 0\,;\,\,x \ne 2} \right)\]. Hỏi sau khi rút gọn biểu thức \[I\] ta được đa thức có bậc là bao nhiêu?
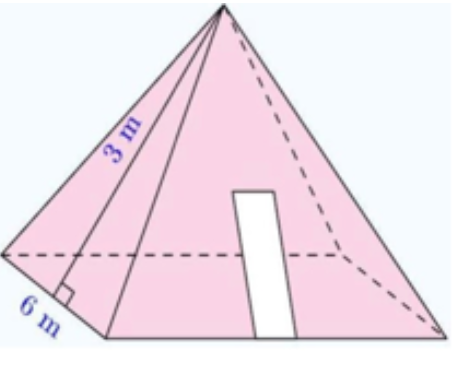
Một kho chứa có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 6 m và trung đoạn là \[3{\rm{ m}}.\] Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ phần cửa có diện tích là \[7{\rm{ }}{{\rm{m}}^{\rm{2}}}.\] Biết rằng cứ mỗi mét vuông sơn cần trả \[50\,\,000\] đồng. Tính số tiền cần trả để hoàn thành việc sơn phủ đó theo đơn vị triệu đồng?
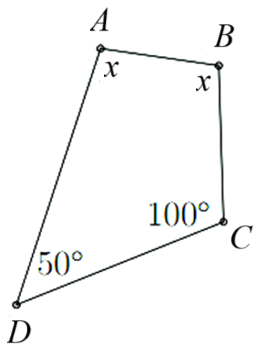
Tìm \(x\) trong hình vẽ dưới đây theo đơn vị độ.
(1,5 điểm) Một xí nghiệp may cứ mỗi tháng thì phải trả tiền lương cho công nhân viên, tiền vật liệu, tiền điện, tiền thuế,… tổng cộng là \[410\,\,000\,\,000\] đồng. Mỗi chiếc áo được bán với giá là \[350\,\,000\] đồng. Gọi số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là \[L\] (đồng) và mỗi tháng xí nghiệp sản xuất được \[a\] chiếc áo.

a) Lập hàm số của \[L\] theo \[a\]. Nếu trong một tháng, công ty bán được \[1\,\,000\] chiếc áo thì công ty lời hay lỗ bao nhiêu?
b) Mỗi tháng phải sản xuất ít nhất bao nhiêu chiếc áo để xí nghiệp không bị lỗ?
c) Hỏi cần phải sản xuất trung bình bao nhiêu chiếc áo mỗi tháng để sau 1 năm, xí nghiệp thu được tiền lời là \[1\,\,380\,\,000\,\,000\] đồng.
(1,0 điểm) Cho tam giác \(ABC\) vuông ở \(A.\) Gọi \(G\) là trung điểm của \(BC.\) Qua \(G\) kẻ \(GE \bot AB\) \(\left( {E \in AB} \right)\) và \(GF \bot AC\) \(\left( {F \in AC} \right).\) Từ \(E\) kẻ đường thẳng song song với \(BF,\) đường thẳng này cắt \(GF\) tại \(I.\)
a) Chứng minh tứ giác \(BEIF\) là hình bình hành.
b) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(AGCI\) là hình vuông.
(0,5 điểm) Cho \({a^3} + {b^3} + {c^3} = 3abc\) và \(a + b + c \ne 0.\) Tính giá trị của biểu thức: \(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}}.\)
Phân tích đa thức \[\left( {{x^2} + 4x + 4} \right) - \left( {x + 2} \right)\] thành nhân tử ta được
\[\left( {x + 2} \right)\left( {x + 1} \right)\].
\[x\left( {x + 2} \right)\].
\[x\left( {x + 3} \right)\].
\[\left( {x + 2} \right)\left( {x + 3} \right)\].
Nhận định nào sau đây là đúng?
Nếu hình chóp có đáy là hình thoi, chân đường cao trùng với tâm hình thoi thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình chữ nhật, chân đường cao trùng với giao điểm của hai đường chéo đáy thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình vuông thì nó là hình chóp đều.
Nếu hình chóp có đáy là tam giác đều, chân đường cao trùng với trọng tâm của tam giác thì nó là hình chóp đều.
Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là
hình thang cân.
hình chữ nhật.
hình bình hành.
hình thoi.








