Bộ 5 đề thi Cuối kì 1 Toán 11 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 5
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho góc lượng giác \(\alpha = - \frac{{5\pi }}{4}\). Khẳng định nào sau đây đúng?
\(\sin \alpha < 0\).
\(\cos \alpha < 0\).
\(\tan \alpha > 0\).
\(\cot \alpha > 0\).
Trong các mệnh đề sau, mệnh đề nào đúng?
\(\sin 2\alpha = 4\sin \alpha .\cos \alpha \).
\(\sin 2\alpha = 2\sin \alpha .\cos \alpha \).
\(\sin 2\alpha = \sin \alpha .\cos \alpha \).
\(\sin 2\alpha = 2{\cos ^2}\alpha - 1\).
Trong các dãy số cho bởi công thức của số hạng tổng quát dưới đây, dãy số nào là dãy số tăng?
\({u_n} = \frac{5}{n}\).
\({u_n} = 2n + 1\).
\({u_n} = 1 - 2n\).
\({u_n} = {\left( { - 1} \right)^n}.n\).
Dãy số nào sau đây không phải là cấp số nhân?
\(1; - 1;1; - 1\).
\(1; - 3;9;10\).
\(1;0;0;0\).
\(32;16;8;4\).
Một người thống kê thời gian thực hiện các cuộc gọi điện thoại của mình (đơn vị: phút) trong một tuần ở bảng sau:

Giá trị đại diện của nhóm \(\left[ {180;240} \right)\) là
\(205\).
\(210\).
\(200\).
\(220\).
Tìm hiểu thời gian xem ti vi trong tuần của một số học sinh (đơn vị: giờ) thu được mẫu số liệu ghép nhóm sau:

Tìm cỡ mẫu của mẫu số liệu trên
\(35\).
\(33\).
\(34\).
\(36\).
Cho điểm \(A\) thuộc mặt phẳng \(\left( P \right)\), mệnh đề nào sau đây đúng?
\(A \subset \left( P \right)\).
\(A \notin \left( P \right)\).
\(A \in \left( P \right)\).
\(A\not \subset \left( P \right)\).
Cho hình tứ diện \(ABCD\). Khẳng định nào sau đây đúng?
\(AC\) và \(BD\) cắt nhau.
\(AC\)và \(BD\) không có điểm chung.
Tồn tại một mặt phẳng chứa \(AC\) và \(BD\).
\(AC\)và \(BD\) song song với nhau.
Trong không gian cho ba mặt phẳng phân biệt \(\left( P \right),\left( Q \right)\) và \(\left( R \right)\). Xét các mệnh đề sau
(I) Nếu mặt phẳng (P) chứa một đường thẳng song song với (Q) thì (P) song song với (Q).
(II) Nếu mặt phẳng (P) chứa hai đường thẳng song song với (Q) thì (P) song song với (Q).
(III) Nếu hai mặt phẳng (P) và (Q) song song với (R) thì (P) song song với (Q).
(IV) Nếu hai mặt phẳng (P) và (Q) cắt (R) thì (P) song song với (Q).
Số mệnh đề đúng là
1.
0.
3.
2.
Trong các mệnh đề sau, mệnh đề nào sai?
Hình lăng trụ có các cạnh bên song song và bằng nhau.
Các mặt bên của hình lăng trụ là các hình bình hành.
Hai mặt đáy của hình lăng trụ là hai đa giác đều.
Hai mặt đáy của hình lăng trụ nằm trên hai mặt phẳng song song.
Cho dãy số \(\left( {{u_n}} \right)\) có \(\lim {u_n} = - 2\), dãy số \(\left( {{v_n}} \right)\) có \(\lim {v_n} = 3\). Tính \(\lim \left( {{u_n} + {v_n}} \right)\).
3.
1.
6.
5.
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(K\) và \({x_0} \in K\). Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) khi nào?
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không tồn tại.
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\).
\(f\left( {{x_0}} \right)\) không tồn tại.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = - 2,d = - 5\).
a) Dãy số \(\left( {{u_n}} \right)\) là một dãy tăng.
b) \({u_2} = - 7\).
c) Số hạng tổng quát \({u_n} = - 5n + 7\).
d) Số \( - 902\) là số hạng thứ 180 của dãy số \(\left( {{u_n}} \right)\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành có tâm là \(O\).
a) Điểm \(O\) không thuộc mặt phẳng \(\left( {SBD} \right)\).
b) \(SA\) và \(BD\) là hai đường thẳng chéo nhau.
c) Giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là đường thẳng đi qua \(S\) và song song với \(AD\).
d) Gọi \(I\) là trung điểm của SB. Khi đó \(OI//\left( {SCD} \right)\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Có bao nhiêu giá trị của \(x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) để hàm số \(y = \cos x\)nhận giá trị bằng \(\frac{1}{2}\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có công bội \(q = 3\) biết \({u_4} = 54\). Tìm số hạng \({u_1}\).
Khảo sát tiền lương tháng của các nhân viên của một văn phòng được ghi lại ở bảng sau:
Lương tháng (triệu đồng) | \(\left[ {6;8} \right)\) | \(\left[ {8;10} \right)\) | \(\left[ {10;12} \right)\) | \(\left[ {12;14} \right)\) |
Số nhân viên | 3 | 6 | 8 | 7 |
Tính mức lương mà nhiều người đạt được nhất (làm tròn kết quả đến hàng phần mười).
Tính giới hạn \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{{5.2}^{n + 2}} - {{2.3}^{n + 2}}}}{{7 + {3^{n + 1}}}}\).
PHẦN II. TỰ LUẬN
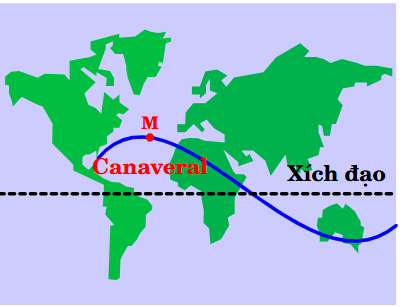
Giả sử một con tàu vũ trụ được phóng lên từ mũi Canaveral ở Mỹ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất như hình mô phỏng bên dưới. Điểm M mô tả cho con tàu, đường thẳng D mô tả cho đường xích đạo. Khoảng cách \(h\) (km) từ \(M\) đến \(\Delta \) được tính theo công thức \(h = \left| d \right|\), trong đó \(d = 4000\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right]\), với \(t\) (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, d > 0 nếu M ở phía trên D, d < 0 nếu M ở phía dưới D. Hãy tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có \(h\) lớn nhất.
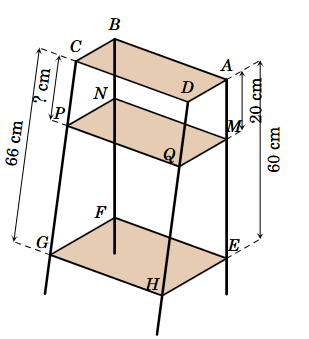
Ông Hai có một kệ gỗ để vật dụng gia đình gồm 2 tầng song song nhau. Để tăng diện tích để vật dụng, ông Hai đóng thêm một mặt gỗ ở giữa hai tầng để trờ thành kệ gỗ 3 tầng. Do đó, ông Hai kí hiệu và đo các kích thước như hình bên dưới. Nếu ông Hai đo đoạn AM = 20 cm thì ông Hai phải đo CP dài bao nhiêu cm để mặt gỗ MNPQ song song với 2 tầng kia. Biết \(AE = 60\;{\rm{cm}}\), CG = 66 cm.
Tại một nhà máy, người ta đo được rằng 80% lượng nước sau khi qua sử dụng được xử lí và tái sử dụng. Với 100 m3 ban đầu được sử dụng tại nhà máy, khi quá trình xử lí và tái sử dụng lặp lại mãi mãi, nhà máy sử dụng được tổng lượng nước là bao nhiêu?








