Bộ 5 đề thi Cuối kì 1 Toán 11 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Khẳng định nào sau đây là sai?
\(\sin \left( {a - b} \right) = \sin a\cos b + \cos a\sin b\).
\(\sin 2a = 2\sin a\cos a\).
\(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\).
\({\cos ^2}\alpha - {\sin ^2}\alpha = \cos 2\alpha \).
Hàm số \(y = \cos x\) là hàm số
Lẻ và tuần hoàn với chu kì \(2\pi \).
Chẵn và tuần hoàn với chu kì \(2\pi \).
Lẻ và tuần hoàn với chu kì \(\pi \).
Chẵn và tuần hoàn với chu kì \(\pi \).
Công thức nào sau đây là đúng với cấp số cộng có số hạng đầu \({u_1}\), công sai \(d,n \ge 2\)?
\({u_n} = {u_1} + \left( {n - 1} \right)d\).
\({u_n} = {u_1} + d\).
\({u_n} = {u_1} + \left( {n + 1} \right)d\).
\({u_n} = {u_1} - \left( {n - 1} \right)d\).
Cho cấp số nhân có \({u_1} = 1;q = 3\). Số hạng thứ 9 của cấp số nhân là
\(19683\).
\(2187\).
\(729\).
\(6561\).
Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tính trung vị của mẫu số liệu ghép nhóm này
\(18,1\).
\(18,5\).
\(17,2\).
\(15,6\).
Chiều cao của 40 vận động viên bóng chuyền được cho trong bảng sau
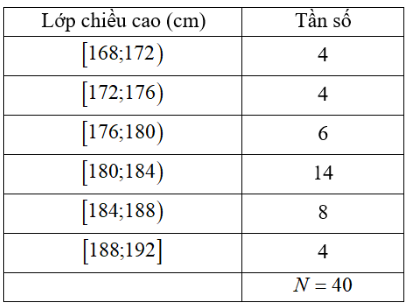
Giá trị đại diện của nhóm [180; 184) là
\(182\).
\(184\).
\(14\).
\(180\).
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,BC\). Giao tuyến của hai mặt phẳng \(\left( {MCD} \right)\) và \(\left( {ADN} \right)\)là
Đường thẳng MN.
Đường thẳng AM.
Đường thẳng DH (H là trọng tâm tam giác ABC).
Đường thẳng BG (G là trọng tâm tam giác ACD).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Hình chiếu song song của điểm \(O\)lên \(\left( {SAD} \right)\) theo phương của đường thẳng \(SB\) là
Điểm A.
Điểm D.
Điểm M là trung điểm của đoạn SA.
Điểm N là trung điểm của đoạn SD.
Phát biểu nào sau đây là sai?
\(\lim {q^n} = 0\left( {\left| q \right| > 1} \right)\).
\(\lim \frac{1}{n} = 0\).
\(\lim \frac{1}{{{n^k}}} = 0\) (k nguyên dương).
\(\lim {u_n} = c\) (\({u_n} = c\) là hằng số).
Hàm số nào sau đây liên tục trên \(\mathbb{R}\).
\(y = 2{x^3} - 3{x^2} + 1\).
\(y = \frac{{x + 1}}{{2x - 1}}\).
\(y = \tan x\).
\(y = \sqrt {2x - 1} \).
Hàm số \(y = \frac{{x + 2}}{{x - 3}}\) gián đoạn tại điểm nào dưới đây?
\({x_0} = 1\).
\({x_0} = - 2\).
\({x_0} = - 1\).
\({x_0} = 3\).
Nếu \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = 4\) thì \(\mathop {\lim }\limits_{x \to 3} \left[ {4 - 3f\left( x \right)} \right]\) bằng
\(9\).
\(8\).
\( - 8\).
\( - 9\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho mẫu số liệu điểm môn Toán của một nhóm học sinh như sau
Điểm | \(\left[ {6;7} \right)\) | \(\left[ {7;8} \right)\) | \(\left[ {8;9} \right)\) | \(\left[ {9;10} \right)\) |
Số học sinh | 8 | 7 | 10 | 5 |
a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm.
b) Cỡ mẫu của mẫu số liệu là 30.
c) Điểm trung bình của các học sinh là 7,9.
d) Mốt của mẫu số liệu là 10.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,N,P\) theo thứ tự là trung điểm của các cạnh \(SB,BC\) và \(SD\).
a) Đường thẳng \(SA\) là giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\).
b) Hai đường thẳng \(MP\) và \(SC\) cắt nhau.
c) Giao tuyến của mặt phẳng \(\left( {MNP} \right)\)và mặt phẳng \(\left( {ABCD} \right)\) là đường thẳng đi qua \(N\) và song song với đường thẳng \(BD\).
d) Biết rằng đường thẳng \(SA\) cắt mặt phẳng \(\left( {MNP} \right)\) tại điểm \(K\). Khi đó \(\frac{{SK}}{{SA}} = \frac{1}{4}\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Phương trình \(\tan \left( {2x + \frac{\pi }{4}} \right) = - \sqrt 3 \) có nghiệm \(x = \frac{{a\pi }}{b} + \frac{{k\pi }}{2}\left( {a;k \in \mathbb{Z};b \in \mathbb{N}*} \right)\); \(\frac{a}{b}\) là phân số tối giản. Tính giá trị của biểu thức \({a^2} + b\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 123;{u_3} - {u_{15}} = 84\). Số hạng \({u_{17}}\) bằng bao nhiêu?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\) là trung điểm của \(SC\). Gọi \(I\) là giao điểm của \(AM\) với mặt phẳng \(\left( {SBD} \right)\). Khi đó \(\overrightarrow {IA} = k\overrightarrow {IM} \). Giá trị của \({k^3}\) bằng bao nhiêu?
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{9 - {x^2}}}{{x - 3}}{\rm{khi}}\;x < 3\\1 - x\;\;\;{\rm{khi}}\;x \ge 3\end{array} \right.\). Biết \(\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = a\) và \(\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = b\). Giá trị của \({a^2} + {b^2}\) bằng bao nhiêu?
PHẦN II. TỰ LUẬN
Trong không gian cho 10 điểm phân biệt, không có ba điểm nào thẳng hàng và không có 4 điểm nào đồng phẳng. Hỏi có bao nhiêu mặt phẳng đi qua ba điểm trong 10 điểm đó?
Người ta thiết kế một cái tháp gồm 10 tầng theo cách sau: Diện tích bề mặt trên của mỗi tầng bằng một nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt trên của tầng 1 bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là 12288 m2. Tính diện tích bề mặt trên cùng của tháp (đơn vị: m2).
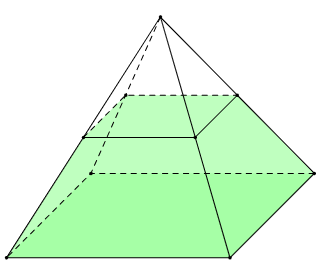
Một khối gỗ có dạng hình chóp có đáy là hình vuông và tất cả các cạnh bằng 0,5 m. Một người muốn thiết kế thành đồ trang trí bằng cách cưa đi phần đỉnh của khối gỗ này và gắn dây đèn trang trí theo các cạnh của khối hình mới (tham khảo hình vẽ). Biết rằng lưỡi cưa đi qua 3 trung điểm của ba cạnh bên của khối gỗ. Chiều dài của dây đèn trang trí là bao nhiêu mét?