Bộ 5 đề thi Cuối kì 1 Toán 11 Cánh diều cấu trúc mới (có tự luận) có đáp án - Đề 4
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mệnh đề nào sau đây là sai?
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\left( {\cos \alpha \ne 0} \right)\).
\(\tan \alpha + \cot \alpha = 2\).
\(\tan \alpha .\cot \alpha = 1\).
Hàm số \(y = \tan x\) tuần hoàn với chu kì là
\(3\pi \).
\(\frac{\pi }{2}\).
\(2\pi \).
\(\pi \).
Cho dãy số \(\left( {{u_n}} \right)\) biết \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = {u_n} + 1\end{array} \right.\) với \(n \ge 1\). Số hạng thứ ba của dãy số là số nào dưới đây?
\(5\).
\(4\).
\(3\).
\(2\).
Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
\({u_n} = 2n + 1\).
\({u_n} = {n^2}\).
\({u_n} = \frac{7}{{3n}}\).
\({u_n} = {3^n}\).
Dãy số nào sau đây có giới hạn bằng 0?
\({\left( {\frac{6}{5}} \right)^n}\).
\({\left( {\frac{5}{2}} \right)^n}\).
\({\left( {\frac{5}{6}} \right)^n}\).
\({5^n}\).
Cho hai hàm số \(f\left( x \right),g\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = 25;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 5\). Giá trị của \(\mathop {\lim }\limits_{x \to - \infty } \frac{{g\left( x \right)}}{{f\left( x \right)}}\) bằng
\(20\).
\(5\).
\( - 5\).
\(25\).
Cho mệnh đề đúng.
Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên một khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại một điểm của khoảng đó.
Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên một khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên một khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại ba điểm của khoảng đó.
Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên một khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại hai điểm của khoảng đó.
Hàm số nào sau đây liên tục trên \(\mathbb{R}\).
\(y = \tan x\).
\(y = {x^2} - 3x + 2024\).
\(y = \sqrt {x - 4} \).
\(y = \sqrt x \).
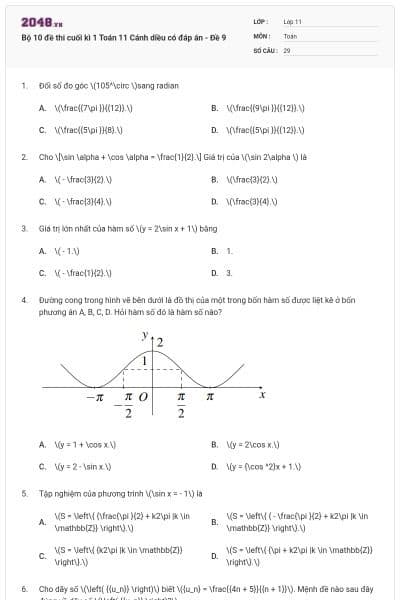
Cho tam giác \(ABC\). Lấy điểm \(M\)trên cạnh \(AC\) kéo dài (như hình)
Mệnh đề nào sau đây là mệnh đề sai?
\(A \in \left( {MBC} \right)\).
\(B \in \left( {ACM} \right)\).
\(M \in \left( {ABC} \right)\).
\(C \in \left( {ABM} \right)\).
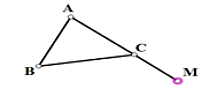
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành (như hình vẽ).
Hai đường thẳng \(SB\) và \(CD\) là hai đường thẳng.
Song song.
Chéo nhau.
Cắt nhau.
Trùng nhau.
Cho đường thẳng d nằm trên mặt phẳng \(\left( Q \right)\). Khi đó mệnh đề nào sau đây sai?
d có hai điểm chung phân biệt thuộc \(\left( Q \right)\).
\(d \subset \left( Q \right)\).
\(M \in d,d \subset \left( Q \right) \Rightarrow M \notin \left( Q \right)\).
d và \(\left( Q \right)\)có vô số điểm chung.
Hai mặt phẳng được gọi là song song với nhau nếu
chúng có hai điểm chung.
chúng có một đường thẳng chung.
chúng có đúng một điểm chung.
chúng không có điểm chung.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho lăng trụ tứ giác \(ABCD.A'B'C'D'\) có hai đáy \(ABCD\) và \(A'B'C'D'\)là hai hình bình hành.
a) Lăng trụ tứ giác \(ABCD.A'B'C'D'\)là hình hộp.
b) Tứ giác \(ABC'D'\) là hình chữ nhật.
c) Đường thẳng \(AD'\)song song với mặt phẳng \(\left( {BDC'} \right)\).
d) Mặt phẳng \(\left( {ACD'} \right)\)song song với mặt phẳng \(\left( {BA'C'} \right)\).
Cho hàm số \(f\left( x \right) = \tan 3x\).
a) Giá trị của hàm số tại \(x = \frac{\pi }{3}\) bằng 0.
b) Hàm số \(f\left( x \right)\) là hàm số lẻ.
c) Tập xác định của hàm số \(f\left( x \right)\) là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{6} + k\pi |k \in \mathbb{Z}} \right\}\).
d) Tổng các nghiệm của phương trình \(\tan 3x = 1\) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{5\pi }}{4}\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Nếu \(a,b\) là hai góc nhọn và \(\sin a = \frac{1}{3},\sin b = \frac{1}{2}\) thì \(\cos 2\left( {a + b} \right)\) có giá trị bằng \(\frac{{7 - m\sqrt 6 }}{n},n \ne 0\). Hãy tính giá trị của \(m + 2n\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và số hạng thứ hai \({u_2} = - 6\). Tính \({u_4}\).
Tìm giới hạn \(\lim \frac{{3{n^2} + n}}{{1 - 2{n^2}}}\).
Cho lăng trụ \(ABC.A'B'C'\). Gọi \(M\) là trung điểm của \(AC\). Gọi \(N\)là hình chiếu song song của điểm \(M\) lên \(\left( {AA'B'} \right)\) theo phương chiếu \(CB\). Tính \(\frac{{MN}}{{BC}}\).
PHẦN II. TỰ LUẬN
Người ta trồng 465 cây trong một khu vườn hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có 2 cây, hàng thứ ba có 3 cây, … cứ tiếp tục trồng như thế cho đến khi hết số cây. Tính số hàng cây của khu vườn.
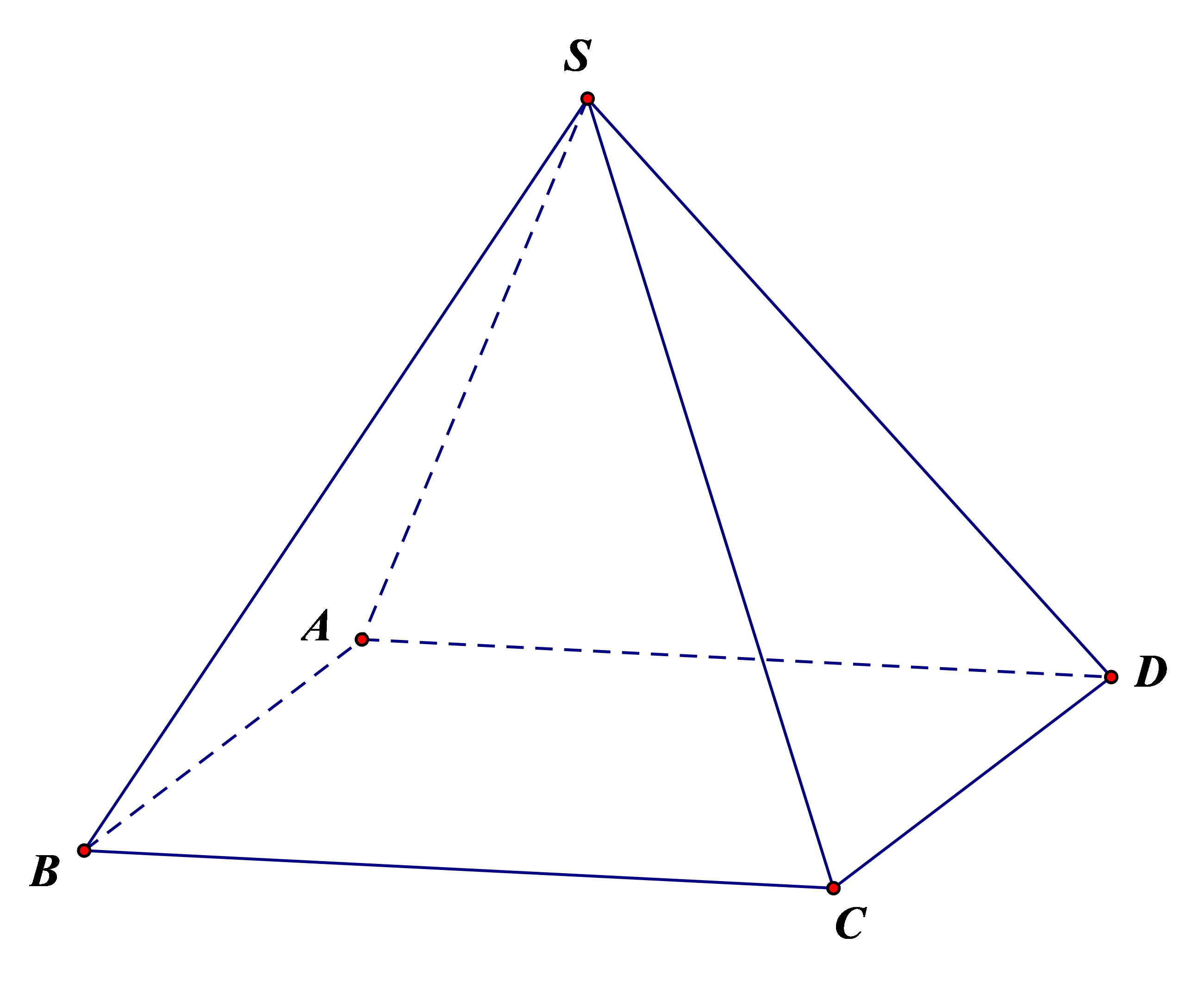
Hình bên dưới là kệ sách gỗ có bốn mặt kệ, với thanh gỗ đứng (xem như đường thẳng d1) và thanh gỗ xiên (xem như đường thẳng d2). Giả sử các mặt kệ xuất hiện ở các vị trí \(A,B,C,D,E,F,G,H\). Biết rằng \(EF = 32\) cm và các điểm \(A,B,C,D\) cách đều nhau. Các mặt kệ đặt song song với mặt đất. Tính độ dài HE.
Từ sảnh tầng 2 của dãy nhà G trường THPT A với độ cao 7,2 m so với mặt sân, một học sinh khối 11 thả một quả bóng cao su xuống sân trường. Giả sử cứ sau mỗi lần chạm đất, quá bóng lại nảy lên một độ cao bằng \(\frac{3}{{10}}\) độ cao mà quả bóng đạt được trước đó. Gọi \({S_n}\) là tổng độ dài quãng đường đi được của quả bóng từ lúc bắt đầu thả quả bóng đến khi quả bóng chạm đất lần thứ \(n\). Nếu quá trình này cứ tiếp tục diễn ra mãi, hay tính tổng quãng đường bóng di chuyển được?