Bộ 5 đề thi Cuối kì 1 Toán 11 Cánh diều cấu trúc mới (có tự luận) có đáp án - Đề 2
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Giá trị \(\tan \frac{{65\pi }}{6}\) bằng
\(\frac{2}{3}\).
\( - \frac{{\sqrt 3 }}{3}\).
\( - \sqrt 3 \).
\(\frac{3}{2}\).
Trong các khẳng định sau, khẳng định nào đúng?
\(\sin \left( {a + b} \right) = \cos a.\cos b + \sin a\sin b\).
\(\sin \left( {a + b} \right) = \sin a.\cos b - \cos a.\sin b\).
\(\sin \left( {a + b} \right) = \cos a.\cos b - \sin a.\sin b\).
\(\sin \left( {a + b} \right) = \sin a.\cos b + \cos a\sin b\).
Trong các dãy số sau dãy số nào là dãy số giảm?
\( - 5; - 4; - 3; - 2; - 1\).
\(0; - 1; - 3; - 5; - 7\).
\(0;3;12;16;19\).
\(24;15;14;16;19\).
Dãy nào sau đây là cấp số cộng?
\(3;3;3;7;10\).
\(2; - 1; - 4; - 7; - 10\).
\(1;4;7;9;1\).
\(1;3;5;7;11\).
Cho dãy số \(\left( {{u_n}} \right)\) với \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - 1} \right) = 0\). Khẳng định nào sau đây đúng?
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0\).
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = - 1\).
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 1\).
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty \).
Cho hàm số \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 3\). Giá trị \(\mathop {\lim }\limits_{x \to + \infty } 4f\left( x \right)\) bằng
\(3\).
\( + \infty \).
\(4\).
\(12\).
Trong không gian, cho ba điểm phân biệt \(A,B,C\) không thẳng hàng. Có bao nhiêu mặt phẳng phân biệt đi qua cả ba điểm trên?
Vô số.
\(1\).
\(2\).
\(3\).
Trong không gian, hai đường thẳng không có điểm chung thì
chéo nhau hoặc song song.
cắt nhau.
song song.
chéo nhau.
Cho hai đường thẳng phân biệt \(a,b\) và mặt phẳng \(\left( \alpha \right)\). Giả sử \(a//b,b//\left( \alpha \right)\). Khi đó
\(a//\left( \alpha \right)\) hoặc \(a \subset \left( \alpha \right)\).
\(a//\left( \alpha \right)\).
\(a\) cắt \(\left( \alpha \right)\).
\(a \subset \left( \alpha \right)\).
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Mặt phẳng \(\left( R \right)\)cắt mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\)lần lượt theo hai giao tuyến a và b. khẳng định nào sau đây sai?
\(a//\left( Q \right)\).
\(b//\left( P \right)\).
\(a//b\).
\(a\) và \(b\) chéo nhau.
Tính chất nào không đúng về hình lăng trụ?
Mặt bên là các hình bình hành.
Các cạnh bên song song và bằng nhau.
Đáy là hai đa giác bằng nhau.
Các cạnh bên đồng quy tạo một điểm.
Qua phép chiếu song song trong không gian, hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
Hình chữ nhật.
Hình bình hành.
Hình thoi.
Hình thang.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(O\). Gọi \(M,N\) lần lượt là trung điểm của \(SB,BC\)
a) Đường thẳng \(AB\) song song với đường thẳng \(CD\).
b) Giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) là đường thẳng qua \(S\) và song song với \(AC\).
c) Đường thẳng \(CD\) song song với mặt phẳng \(\left( {OMN} \right)\).
d) Hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {OMN} \right)\) song song.
Cho cấp số nhân \(\left( {{u_n}} \right)\) gồm các số hạng 5; 10; 20; …; 163840.
a) Số hạng đầu và công bội của cấp số nhân lần lượt là \({u_1} = 5;q = 5\).
b) Số hạng tổng quát của cấp số nhân là \({u_n} = {5.5^{n - 1}}\).
c) Số hạng thứ năm của cấp số nhân là \({u_5} = 80\).
d) Cấp số nhân đã cho là dãy số hữu hạn gồm có 15 số hạng.
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Biểu thức thu gọn của biểu thức \(A = \frac{{\sin 2a + \sin 5a - \sin 3a}}{{1 + \cos a - 2{{\sin }^2}2a}}\) bằng \(m\sin \left( {na} \right)\) với \(m,n \in \mathbb{N}\). Tính \(m + n\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = - 3\) và \(q = 2\). Tìm số hạng thứ 6 của cấp số nhân.
Giới hạn của hàm số \(L = \mathop {\lim }\limits_{x \to 5} \frac{{\sqrt {x + 4} - 3}}{{{x^2} - 25}} = \frac{1}{a}\). Tìm \(a\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(N\) là trung điểm của \(SA\), \({G_1},{G_2}\) lần lượt là trọng tâm của \(\Delta SAB,\Delta SAD\). Khi đó \(\frac{{{G_1}{G_2}}}{{BD}} = \frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản). Tính \(a - b\).
PHẦN II. TỰ LUẬN
Giả sử khi một con sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số \(h\left( t \right) = 80\cos \left( {\frac{\pi }{{2024}}t} \right) + 10\), trong đó \(h\left( t \right)\) là độ cao tính bằng cm trên mực nước biển trung bình tại thời điểm \(t\) giây. Tính chiều cao của sóng (cm) (là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng).
Anh Minh muốn làm kệ để rubic có dạng như hình, nên đã thiết kế bằng việc tạo ra một hình chóp tam giác sau đó cắt phần đỉnh như hình vẽ.

Cụ thể anh Minh làm 1 hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) có \(AB = AC = 5\) cm, \(\widehat {BAC} = 30^\circ \). Sau đó dựng mặt phẳng \(\left( P \right)\) song song với \(\left( {ABC} \right)\) cắt đoạn \(SM\) tại \(M\) sao cho \(SM = 2MA\) rồi cắt để tạo sản phẩm. Hỏi diện tích thiết diện sau khi cắt thành sản phẩm hoàn chỉnh là bao nhiêu?
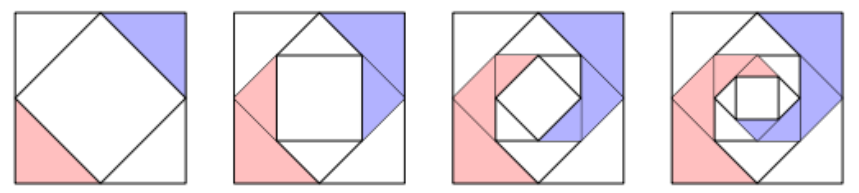
Một thợ thủ công muốn vẽ trang trí một tấm bìa hình vuông có độ dài cạnh bằng 4 mét. Người thợ thủ công quyết định vẽ các hình vuông lên tấm bìa bằng cách: hình vuông mới có các đỉnh là trung điểm các cạnh của hình vuông ban đầu và tô kín màu lên hai tam giác đối diện (như hình vẽ bên dưới). Giả sử quá trình vẽ và tô theo quy luật đó được lặp lại vô hạn lần. Tổng diện tích mà người thợ thủ công đó tô được là bao nhiêu mét vuông?