Bộ 5 đề thi cuối kì 1 Toán 10 Kết nối tri thức cấu trúc mới có đáp án - Đề 05
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phát biểu nào sau đây là mệnh đề?
Em thích học môn Toán không?
Hãy làm bài kiểm tra nghiêm túc!
Đông Phú là thị trấn của huyện Quế Sơn.
\(3x + 5\) chia hết cho 7.
Cho b là một phần tử của tập hợp S . Mệnh đề nào dưới đây đúng?
\(b \subset S\).
\(b \in S\).
\(S \subset b\).
\(\left\{ b \right\} \in S\).
Cho \(M = \left[ { - 2;3} \right],N = \left( {0;7} \right)\). Tập \(M \cup N\) là
\(\left[ { - 2;7} \right)\).
\(\emptyset \).
\(\left( {0;3} \right]\).
\(\left[ { - 2;0} \right)\).
Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\},B = \left\{ {2;3;5;6;7} \right\}\). Khi đó \(A \cap B = ?\)
\(\left\{ {2;3} \right\}\).
\(\left\{ 3 \right\}\).
\(\left\{ {3;5} \right\}\).
\(\left\{ {2;3;5} \right\}\).
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất 2 ẩn \(x,y\)?
\(\left\{ \begin{array}{l}xy - y < - 3\\x + 2y \ge - 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - y < - 3\\x + {5^2}y \ge - 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - y < - 3\\{x^2} + 2xy \ge - 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - {y^2} < - 3\\x + y \ge - 4\end{array} \right.\).
Biết miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y \ge m\\x - 5y < m + 2\end{array} \right.\) chứa gốc tọa độ \(O\left( {0;0} \right)\). Có bao nhiêu giá trị nguyên của tham số \(m\) thỏa mãn hệ bất phương trình trên?
1.
4.
3.
2.
Chọn công thức đúng trong các đáp án sau:
\(S = \frac{1}{2}bc\sin A\,.\)
\(S = \frac{1}{2}ac\sin A\,.\)
\(S = \frac{1}{2}bc\sin B\,.\)
\(S = \frac{1}{2}bc\sin B\,.\)
Tam giác \(ABC\) có \(a = 21,{\rm{ }}b = 17,{\rm{ }}c = 10\). Diện tích của tam giác \(ABC\) bằng:
\[{S_{\Delta ABC}} = 16\].
\[{S_{\Delta ABC}} = 48\].
\[{S_{\Delta ABC}} = 24\].
\[{S_{\Delta ABC}} = 84\].
Gọi \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\) của hình bình hành \(ABCD\). Đẳng thức nào sau đây là đẳng thức sai?
\(\overrightarrow {OA} = \overrightarrow {OC} \).
\(\overrightarrow {AB} = \overrightarrow {DC} \).
\(\overrightarrow {CB} = \overrightarrow {DA} \).
\(\overrightarrow {OB} = \overrightarrow {DO} \).
Cho tam giác \(ABC\), gọi \(M\) là trung điểm của \(BC\) và \(G\) là trọng tâm của tam giác \(ABC\). Mệnh đề nào sau đây đúng?
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AM} \).
\(\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
\(\overrightarrow {AG} = \frac{3}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
\(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AM} \).
Làm tròn số của \(2,57656\) đến hàng phần chục ta được kết quả là
\(2,57\).
\(2,58\).
\(2,5\).
\(2,6\).
Cho số gần đúng \(a = 869265\) với độ chính xác \(d = 50\). Số quy tròn của số \(a\) là
\(869300\).
\(869270\).
\(869200\).
\(869260\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ \(A\) thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ \(B\) thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20 . Gọi \(x,y\) theo thứ tự là số lần người chơi chọn được chữ \(A\) và chữ \(B\). Khi đó:
a) Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
b) Bất phương trình bậc nhất hai ẩn \(x,y\) trong tình huống người chơi chiến thắng là \(3x - y \ge 18.\)
c) Người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
d) Người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 4 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Cho \(\sin \alpha = \frac{2}{3}\left( {90^\circ < \alpha < 180^\circ } \right)\,\)
a) \(\cos \alpha < 0\).
b) \(\cos \alpha = - \frac{{\sqrt 5 }}{3}\).
c) \(\frac{{\sin \alpha + 2\sqrt 5 \cos \alpha }}{{2\sin \alpha + \sqrt 5 \cos \alpha }} = \frac{4}{3}\).
d) \(\frac{{\sin \alpha - \cos (180^\circ - \alpha )}}{{\sin \left( {90^\circ - \alpha } \right) + \sin (180^\circ - \alpha )}} = - 1\).
Trong hệ tọa độ \(Oxy\), cho bốn điểm \(A\left( {1;1} \right),B\left( {2; - 1} \right),C\left( {4;3} \right),D\left( {3;5} \right)\).
a) \(\overrightarrow {AB} = \left( {1; - 2} \right)\).
b) \(G\left( {2;\frac{5}{3}} \right)\) là trọng tâm tam giác \(BCD\).
c) \(\overrightarrow {AB} ,\overrightarrow {CD} \) cùng phương.
d) Hai vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) vuông góc với nhau.
Trong một cuộc thi nghề, người ta ghi lại thời gian (đơn vị: phút) hoàn thành một sản phẩm của một số thí sinh ở bảng sau
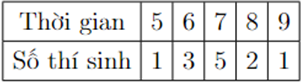
a) Trung vị của mẫu số liệu \({Q_2} = 7\).
b) Mốt của mẫu số liệu \({M_o} = 7\).
c) Khoảng tứ phân vị \({\Delta _Q} = 0,5\).
d) Độ lệch chuẩn của mẫu số liệu là \(\frac{{155}}{{144}}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một nhà phân phối bánh gạo có hai nhà kho ở phía Đông và phía Tây của thành phố. Kho ở phía Đông có \(80\) thùng bánh gạo, kho ở phía Tây có \(45\) thùng bánh gạo. Sáng thứ Hai đầu tuần, đại lí \(A\) cần \(50\) thùng bánh gạo, đại lí \(B\) cần \(70\) thùng bánh gạo. Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Đông là \(10\) nghìn đồng cho đại lí \(A\) và \(12\) nghìn đồng cho đại lí \(B\). Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Tây là \(9\) nghìn đồng cho đại lí \(A\) và \(11\) nghìn đồng cho đại lí \(B\). Chi phí vận chuyển là nhỏ nhất nhà phân phối cần phải trả là bao nhiêu nghìn đồng?
Cho tam giác \(ABC\) có \(AB = 4\;{\rm{cm}},\,\,\widehat A = 40^\circ ,\,\,\widehat C = 60^\circ \). Diện tích tam giác \(ABC\) bằng bao nhiêu \({\rm{c}}{{\rm{m}}^{\rm{2}}}\)?( làm tròn đến hàng phần trăm).
Để đo chiều cao của một cột cờ trên đỉnh một toà nhà anh Bắc đã làm như sau: Anh đứng trên một đài quan sát có tầm quan sát cao 5 m so với mặt đất, khi quan sát anh đo được góc quan sát chân cột là \(40^\circ \) và góc quan sát đỉnh cột là \(50^\circ \), khoảng cách từ vị trí quan sát đến tòa nhà là \(18{\rm{m}}\). Tổng chiều cao cột cờ và chiều cao của toà nhà là bao nhiêu mét? (Làm tròn đến hàng phần mười).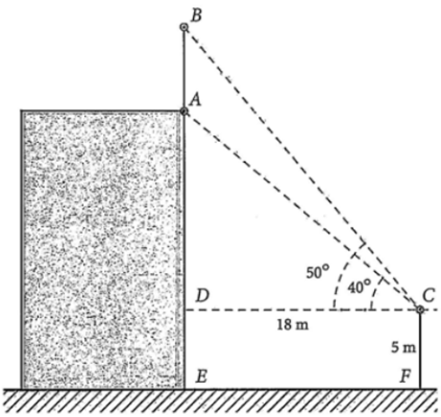
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động vào một vật đặt tại điểm \(O\). Biết hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều có cường độ là 20 N và chúng hợp với nhau một góc \(80^\circ \). Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu Newton (kết quả làm tròn đến hàng phần trăm)?
Trong mặt phẳng với hệ trục tọa độ \(Oxy\); cho tam giác \(ABC\) có \(A\left( {5;8} \right),B\left( {7;6} \right)\) và trọng tâm là \(G\left( {\frac{{10}}{3};\frac{{17}}{3}} \right)\). Giả sử \(N\left( {a;b} \right)\) trên trục \(Ox\) sao cho tam giác \(NBC\) vuông cân tại \(N\). Tính \(a + b\).
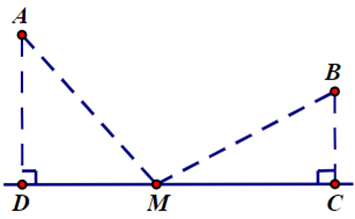
Hai đảo \(A\) và \(B\) cách bờ một khoảng \(AD = 30\)km và \(BC = 20\) km (như hình vẽ). Người ta muốn dựng một trạm phát sóng\(M\) trên bờ \(DC\) sao cho khoảng cách từ trạm phát sóng đến hai đảo bằng nhau. Biết khoảng cách giữa hai vị trí \(D\) và \(C\) bằng \(50\) km. Tính khoảng cách từ trạm phát sóng đến hai đảo (đơn vị km) (kết quả làm tròn đến hàng phần trăm).