Bộ 5 đề thi Cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 4
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các câu sau, câu nào là mệnh đề?
\(x + 2 = 5\).
Lớp 10A1 có bao nhiêu học sinh?
\({x^2} < 4\).
Số 5 là số nguyên tố.
Liệt kê các phần tử của tập hợp \(X = \left\{ {x \in \mathbb{Z}|2{x^2} - 5x + 3 = 0} \right\}\).
\(X = \left\{ {1;\frac{3}{2}} \right\}\).
\(X = \left\{ 1 \right\}\).
\(X = \left\{ 0 \right\}\).
\(X = \left\{ {\frac{3}{2}} \right\}\).
Cặp số nào sau đây không là nghiệm của bất phương trình \(2x + y - 7 > 0\).
\(\left( {3;2} \right)\).
\(\left( {5; - 1} \right)\).
\(\left( {4;0} \right)\).
\(\left( { - 2;5} \right)\).
Hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}0x + 0y > - 4\\4x + y \le 2\end{array} \right.\).
\(\left\{ \begin{array}{l}2x - 5y \ge 2\\\frac{3}{x} - y \le - 1\end{array} \right.\).
\(\left\{ \begin{array}{l}{x^2} + {y^3} > 4\\2x - 5y \le 1\end{array} \right.\).
\(\left\{ \begin{array}{l}3x + 7y \le 11\\5x - y < 5\end{array} \right.\).
Tìm tập xác định của hàm số \(f\left( x \right) = \frac{{2x - 1}}{{x + 3}}\).
\(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\).
\(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
\(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
\(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Trục đối xứng của đồ thị hàm số sau đây có phương trình là
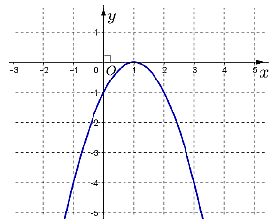
\(x = 1\).
\(y = 1\).
\(y = 0\).
\(x = - 1\).
Cho α và β là hai góc bù nhau. Trong các khẳng định sau, khẳng định nào sai?
\(\cot \alpha = \cot \beta \).
\(\cos \alpha = - \cos \beta \).
\(\sin \alpha = \sin \beta \).
\(\tan \alpha = - \tan \beta \).
Cho tam giác ABC có \(BC = a;CA = b;AB = c\). Mệnh đề nào dưới đây đúng?
\({a^2} = {b^2} + {c^2} + 2bc.\cos A\).
\({c^2} = {a^2} + {b^2} - 2ab\cos C\).
\(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}}\).
\({b^2} = {a^2} + {c^2}\).
Phát biểu nào sau đây là sai?
Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
Hai vectơ cùng phương thì cùng hướng.
Hai vectơ cùng hướng với một vectơ khác vectơ không thì chúng cùng hướng.
Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Cho bốn điểm bất kỳ A, B, C, O. Mệnh đề nào sau đây là đúng?
\(\overrightarrow {OA} = \overrightarrow {OB} - \overrightarrow {BA} \).
\(\overrightarrow {OA} = \overrightarrow {CA} + \overrightarrow {CO} \).
\(\overrightarrow {BC} - \overrightarrow {AC} + \overrightarrow {AB} = \overrightarrow 0 \).
\(\overrightarrow {BA} = \overrightarrow {OB} - \overrightarrow {OA} \).
Số quy tròn của số gần đúng \(a\) biết \(\overline a = 234710 \pm 200\) là
235000.
234910.
234500.
234000.
Khoảng tứ phân vị\({\Delta _Q}\) là
\({Q_2} - {Q_1}\).
\({Q_3} - {Q_2}\).
\({Q_3} + {Q_1}\).
\({Q_3} - {Q_1}\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình vẽ.
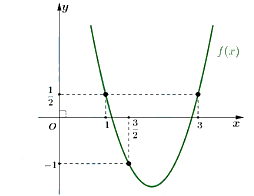
Khi đó:
a) \(f\left( 1 \right) = 1\).
b) \(a > 0\).
c) \(a + b + c > 1\).
d) \(a - b = 10\).
Thời gian chờ xe buýt (đơn vị: phút) của 13 học sinh tại một bến xe buýt được thống kê như sau:
1 | 3 | 6 | 4 | 25 | 8 | 10 | 12 | 15 | 6 | 3 | 5 | 7 |
a) Giá trị lớn nhất của mẫu số liệu là 25.
b) Khoảng biến thiên của mẫu số liệu là 25.
c) Trung vị của mẫu số liệu là 5.
d) Khoảng tứ phân vị của mẫu số liệu là \({\Delta _Q} = 7,5\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho các tập hợp \(A = \left\{ {x \in \mathbb{Z}|\left| x \right| < 3} \right\},B = \left\{ {0;1;3} \right\},C = \left\{ {x \in \mathbb{N}|\left( {{x^2} - 4x + 3} \right)\left( {{x^2} - 4} \right) = 0} \right\}\). Tìm số phần tử của \(\left( {A\backslash B} \right) \cup C\).
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình vẽ.
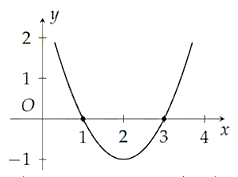
Tìm tất cả các giá trị ngyên của \(x\) để \(f\left( x \right) < 0\).
Cho \(\tan x = \frac{1}{2}\). Tính giá trị của biểu thức \(P = 25\left( {{{\sin }^4}x + {{\cos }^4}x} \right)\).
Một cơ sở chăn nuôi gia cầm tiến hành nuôi thử nghiệm giống gà đẻ trứng mới. Khi gà đã cho trứng họ tiến hành khảo sát với 20 quả được cân nặng (gam) như sau
40 | 42 | 36 | 38 | 40 | 42 | 29 | 48 | 43 | 43 |
41 | 41 | 39 | 44 | 45 | 41 | 40 | 39 | 42 | 41 |
Trong mẫu số liệu trên hãy tính tích các giá trị bất thường.
PHẦN II. TỰ LUẬN
Một nhà máy dự tính sản xuất hai loại bột cà phê hòa tan (loại I và loại II) từ 15 tấn cà phê hạt và 5 tấn hương liệu tổng hợp. Biết để sản xuất một tấn bột cà phê loại I cần 3 tấn cà phê hạt và 0,5 tấn hương liệu tổng hợp, khi bán lãi được 18 triệu đồng. Để sản xuất một tấn bột cà phê loại II cần 2 tấn cà phê hạt và 1 tấn hương liệu tổng hợp, khi bán lãi được 14 triệu đồng. Biết rằng sản phẩm của nhà máy luôn được tiêu thụ hết. Với lượng nguyên liệu như trên, nhà máy có thể thu được số tiền lãi lớn nhất là bao nhiêu triệu đồng?
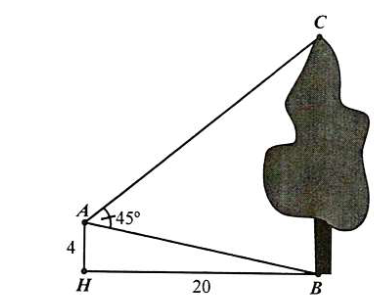
Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết AH = 4 m, HB = 20 m, \(\widehat {BAC} = 45^\circ \). Tính chiều cao của cây?
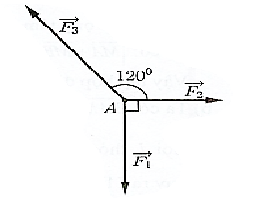
Một chất điểm A chịu tác dụng của ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) như hình vẽ biết chất điểm A đang ở trạng thái cân bằng. Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) biết rằng lực \(\overrightarrow {{F_1}} \) có độ lớn 12 N.