Bộ 5 đề thi Cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 2
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho số tự nhiên \(n\). Xét mệnh đề: “Nếu số tự nhiên \(n\) có chữ số tận cùng bằng 4 thì \(n\) chia hết cho 2”. Mệnh đề đảo của mệnh đề đó là
Nếu số tự nhiên \(n\) chia hết cho 2 thì \(n\) có chữ số tận cùng bằng 4.
Nếu số tự nhiên \(n\) có chữ số tận cùng bằng 4 thì \(n\) không chia hết cho 2.
Nếu số tự nhiên \(n\) chia hết cho 2 thì \(n\) không có chữ số tận cùng bằng 4.
Nếu số tự nhiên \(n\) không chia hết cho 2 thì \(n\) có chữ số tận cùng bằng 4.
Cho tập hợp \(A = \left\{ {0;2} \right\}\). Khẳng định nào sau đây sai?
\(\left\{ 0 \right\} \subset A\).
\(2 \subset A\).
\(\emptyset \subset A\).
\(0 \in A\).
Cho \(X = \left[ { - 1;3} \right];Y = \left( {2;5} \right)\). Tập hợp nào sau đây bằng \(X \cup Y\)?
\(\left( {2;3} \right]\).
\(\left[ { - 1;5} \right)\).
\(\left( {3;5} \right)\).
\(\left[ { - 1;2} \right]\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}|{x^2} - 2x = 0} \right\}\), \(B = \left\{ {x \in \mathbb{Z}|1 < \left| x \right| \le 2} \right\}\). Tìm tập hợp \(A\backslash B\).
\(A\backslash B = \left\{ { - 2;0;2} \right\}\).
\(A\backslash B = \left\{ 2 \right\}\).
\(A\backslash B = \left\{ 0 \right\}\).
\(A\backslash B = \left\{ { - 2} \right\}\).
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(2x - 3y - 6z < 0\).
\(x - xy + 1 \ge 0\).
\(\left( {x - y} \right)\left( {x + y} \right) > 2\).
\(x - 3y \le 2\).
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\)?
\(\left( { - 1;4} \right)\).
\(\left( { - 2;4} \right)\).
\(\left( {0;0} \right)\).
\(\left( { - 3;4} \right)\).
Tập xác định D của hàm số \(y = \sqrt {3x - 1} \) là
\(D = \left( {0; + \infty } \right)\).
\(D = \left[ {0; + \infty } \right)\).
\(D = \left[ {\frac{1}{3}; + \infty } \right)\).
\(D\left( {\frac{1}{3}; + \infty } \right)\).
Trục đối xứng của parabol \(\left( P \right):y = {x^2} - 4x + 2024\) là
\(x = 4\).
\(x = - 4\).
\(x = - 2\).
\(x = 2\).
Rút gọn biểu thức \(S = \cos \left( {90^\circ - x} \right)\sin \left( {180^\circ - x} \right) - \sin \left( {90^\circ - x} \right)\cos \left( {180^\circ - x} \right)\).
\(S = 0\).
\(S = {\sin ^2}x - {\cos ^2}x\).
\(S = 1\).
\(S = 2\sin x\cos x\).
Cho tam giác ABC có AB = 10, AC = 9, \(\cos \widehat {BAC} = \frac{3}{5}\). Tính diện tích S của tam giác ABC?
\(S = 32\).
\(S = 36\).
\(S = 40\).
\(S = 27\).
Cho hình bình hành ABCD tâm O. Hỏi vectơ \(\overrightarrow {AO} - \overrightarrow {DO} \) bằng vectơ nào trong các vectơ sau
\(\overrightarrow {BA} \).
\(\overrightarrow {BC} \).
\(\overrightarrow {DC} \).
\(\overrightarrow {AC} \).
Cho tam giác ABC, lấy điểm I trên cạnh AC sao cho \(\overrightarrow {AC} - 3\overrightarrow {IC} = \overrightarrow 0 \). Biểu diễn \(\overrightarrow {BI} \) theo hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \). Khẳng định nào sau đây đúng?
\(\overrightarrow {BI} = \frac{1}{3}\overrightarrow {BA} - \frac{2}{3}\overrightarrow {BC} \).
\(\overrightarrow {BI} = \frac{2}{3}\overrightarrow {BA} - \frac{1}{3}\overrightarrow {BC} \).
\(\overrightarrow {BI} = \frac{1}{3}\overrightarrow {BA} + \frac{2}{3}\overrightarrow {BC} \).
\(\overrightarrow {BI} = - \overrightarrow {BA} + \frac{3}{4}\overrightarrow {AC} \).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho DABC cân tại A có AB = a và \(\widehat A = 30^\circ \). M và N lần lượt là trung điểm của AB và AC.
a) \(\overrightarrow {MN} = \overrightarrow {BC} \).
b) \(\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {MN} } \right|\).
c)\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = 30^\circ \).
d) \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{\sqrt 3 }}{2}{a^2}\).
Trong một tuần, nhiệt độ cao nhất trong ngày (đơn vị °C) tại hai thành phố Hà Nội và Điện Biên như sau:
Hà Nội | 23 | 25 | 28 | 28 | 32 | 33 | 35 |
Điện Biên | 16 | 24 | 26 | 25 | 26 | 27 | 28 |
Khi đó:
a) Khoảng biến thiên nhiệt độ của mẫu số liệu Hà Nội bằng 12.
b) Khoảng biến thiên nhiệt độ trong tuần của Hà Nội và Điện Biên là giống nhau.
c) Trung vị của mẫu số liệu Điện Biên bằng 25.
d) Từ kết quả phương sai của hai mẫu số liệu ta nhận thấy nhiệt độ trong một tuần của Hà Nội đồng đều hơn ở Điện Biên.
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Tính \(\tan 45^\circ + \cot 135^\circ \).
Cho hai vectơ \(\overrightarrow {AB} ,\overrightarrow {MN} \) như hình vẽ bên.
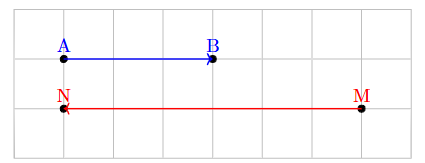
Khi đó \(\overrightarrow {MN} = a\overrightarrow {AB} ,a \in \mathbb{Z}\). Tìm \(a\).
Cho hình thoi ABCD tâm O, \(\widehat {BAC} = 60^\circ \). Gọi M là trung điểm AD và G là trọng tâm của tam giác ABC. Biết \(\overrightarrow {GM} = \frac{m}{3}\overrightarrow {BA} + \frac{n}{6}\overrightarrow {BC} \). Tính tổng \(m + n\).
Sau khi học xong bài “Hệ thức lượng trong tam giác” giáo viên yêu cầu học sinh thực hành đo chiều cao của dãy nhà học 3 tầng. Bạn An đo được chiều cao của dãy nhà là 9,6 m. Sai số tương đối của phép đo là bao nhiêu phần trăm, biết chiều cao thực tế của dãy nhà là 10 m?
PHẦN II. TỰ LUẬN
Một hộ nông dân dự định trồng cây đào và cây bưởi trên diện tích 4 ha. Trên diện tích mỗi ha, nếu trồng đào thì cần 10 công và thu 2 triệu đồng, nếu trồng bưởi thì cần 15 công và thu 2,5 triệu đồng. Số tiền nhiều nhất mà hộ nông dân thu được là bao nhiêu triệu đồng, biết rằng tổng số công không quá 45 công?
Gia đình An dự định kéo đường dây điện thành một hình tròn ngoại tiếp sân chơi hình tam giác có độ dài các cạnh là 20 m, 28 m, 32 m. Độ dài đường dây điện ít nhất nhà An cần dùng là bao nhiêu mét?
Độ cao của quả bóng golf tính theo thời gian có thể được xác định bằng một hàm bậc hai. Với các thông số cho trong bảng sau, hãy xác định độ cao quả bóng đạt được tại thời điểm 3 giây?
Thời gian (giây) | 0 | 0,5 | 1 | 2 |
Độ cao (mét) | 0 | 28 | 48 | 64 |