Bộ 5 đề thi Cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\). Số tập con có hai phần tử của A là
10.
5.
20.
15.
Cho hai tập hợp \(X = \left\{ {1;2;4;7;9} \right\}\) và \(Y = \left\{ { - 1;0;7;10} \right\}\). Tập hợp \(X \cup Y\) có bao nhiêu phần tử?
10.
7.
8.
9.
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau
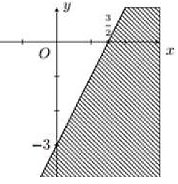
\(2x - y \le 3\).
\(x + y \ge 3\).
\(x - y \ge 3\).
\(x + 2y \ge 3\).
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + y > 0\\x - 3y < 6\\x - y \ge - 4\end{array} \right.\) chứa điểm nào sau đây?
\(M\left( {1;1} \right)\).
\(O\left( {0;0} \right)\).
\(N\left( {1; - 3} \right)\).
\(P\left( { - 1; - 7} \right)\).
Tập xác định của hàm số \(y = \frac{{3x + 4}}{{\sqrt {x - 1} }}\) là
\(\mathbb{R}\backslash \left\{ 1 \right\}\).
\(\mathbb{R}\).
\(\left( {1; + \infty } \right)\).
\(\left[ {1; + \infty } \right)\).
Cho parabol \(y = a{x^2} + bx + 4\) có trục đối xứng là đường thẳng \(x = \frac{1}{3}\) và đi qua điểm \(A\left( {1;3} \right)\). Tổng giá trị \(a + 2b\) là
\( - \frac{1}{2}\).
\(1\).
\(\frac{1}{2}\).
\( - 1\).
Cho góc \(\alpha \left( {0^\circ < \alpha < 180^\circ } \right)\) thỏa mãn \(\cot \alpha = - \frac{1}{2}\). Giá trị \(\cos \alpha \) bằng
\( - \frac{{\sqrt 5 }}{5}\).
\( - \frac{{\sqrt 5 }}{2}\).
\( - \frac{{\sqrt 5 }}{3}\).
\(\frac{{\sqrt 5 }}{5}\).
Cho tam giác ABC có bán kính đường tròn ngoại tiếp tam giác là R. Khẳng định nào dưới đây đúng?
\(R = \frac{{AB}}{{\sin C}}\).
\(R = \frac{{AB}}{{2\sin C}}\).
\(R = \frac{{AB}}{{\cos C}}\).
\(R = \frac{{AB}}{{2\cos C}}\).
Cho ba điểm M, N, P. Vectơ \(\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} \) bằng vectơ nào dưới đây?
\(\overrightarrow {PN} \).
\(\overrightarrow {PM} \).
\(\overrightarrow {MP} \).
\(\overrightarrow {NM} \).
Cho tam giác ABC, gọi M là trung điểm của BC và G là trọng tâm của tam giác ABC. Câu nào sau đây đúng?
\(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \).
\(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GA} \).
\(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GM} \).
\(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} \).
Cho DABC có AB = 5, AC = 8, \(\widehat A = 60^\circ \). Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng
\(40\sqrt 3 \).
\(20\sqrt 3 \).
40.
20.
Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được các số liệu sau: Giá trị nhỏ nhất bằng 2,5; tứ phân vị thứ nhất \({Q_1} = 36\); tứ phân vị thứ hai \({Q_2} = 60\); tứ phân vị thứ ba \({Q_3} = 100\); giá trị lớn nhất bằng 205. Khoảng tứ phân vị của mẫu số liệu này là
\(64\).
14.
202,5.
100,875.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số bậc hai \(y = f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình vẽ
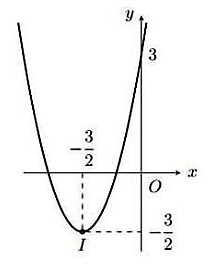
a) Đồ thị hàm số có trục đối xứng \(x = - \frac{3}{2}\).
b) Giá trị lớn nhất của hàm số là \( - \frac{3}{2}\).
c) Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt.
d) \(a > 0;b < 0;c > 0\).
Điểm trung bình môn học kì I của hai bạn An và Bình được cho như bảng
| Toán | Vật lí | Hóa học | Ngữ Văn | Lịch Sử | Địa lí | Tin học | Tiếng Anh |
An | 9,2 | 8,7 | 9,5 | 6,8 | 8,0 | 8,0 | 7,3 | 6,5 |
Bình | 8,2 | 8,1 | 8,0 | 7,8 | 8,3 | 7,9 | 7,6 | 8,1 |
a) Khoảng biến thiên điểm của bạn An là .
b) Bạn An học đều hơn bạn Bình.
c) Điểm trung bình môn học kì I của bạn Bình là 8,0.
d) Phương sai của mẫu số liệu về điểm trung bình học kỳ I của bạn An là 1,022.
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho góc \(\alpha \) thỏa mãn \(\cos \alpha = 0,2\) và \(0^\circ < \alpha < 90^\circ \). Giá trị của \(\cos \left( {180^\circ - \alpha } \right)\) bằng bao nhiêu?
Cho hai điểm M, N thỏa mãn \(\overrightarrow {MN} .\overrightarrow {NM} = - 4\). Tính MN.
Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Khi đó \(\overrightarrow {AK} = m\overrightarrow {AB} + n\overrightarrow {AC} \). Tính \(m + 3n\).
Cho mẫu số liệu 15; 20; 1; 2; 4; 6; 7; 5. Tìm khoảng tứ phân vị của mẫu số liệu trên.
PHẦN II. TỰ LUẬN
Sau dịp Tết Trung thu, gia đình bạn Nam hoàn thành việc sản xuất bánh trung thu và còn dư khá nhiều nguyên liệu như bột nếp, đậu xanh, đường, dầu ăn, lá nếp và tinh dầu bưởi. Gia đình dự kiến sử dụng các nguyên liệu dư đó và mua thêm cốm tươi, dừa tươi để làm bánh Cốm và bánh Xu xê mang đi bán lấy lãi. Biết rằng gia đình bạn Nam đã mua thêm 5 kg cốm tươi và 3 kg dừa sợi. Ngoài các nguyên liệu còn dư ở trên, để sản xuất ra một hộp bánh cốm cần 0,2 kg cốm tươi và 0,1 kg dừa sợi. Để sản xuất ra một hộp bánh Xu xê cần 0,1 kg cốm tươi và 0,1 kg dừa sợi. Mỗi hộp bánh Cốm bán ra được lãi là 6 nghìn đồng và mỗi hộp bánh Xu xê bán ra được lãi 5 nghìn đồng. Mẹ của bạn Nam giao cho Nam lập kế hoạch sản xuất. Để thu được số tiền lãi cao nhất thì cần sản xuất bao nhiêu hộp bánh cốm và bao nhiêu hộp bánh Xu xê?
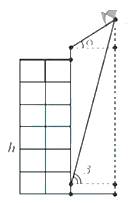
Một người A đứng ở đỉnh của một tòa nhà cao h = 18 m quan sát một chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của người A tới chiếc diều và phương nằm ngang) là \(\alpha = 40^\circ \), khoảng cách từ đỉnh tòa nhà đến mặt người A là 1,6 m. Cùng lúc đó ở dưới chân tòa nhà người B cũng quan sát một chiếc diều, nhận thấy góc nâng là \(\beta = 80^\circ \), khoảng cách từ mặt đất đến mắt người B là 1,5 m. Hỏi chiếc diều bay cao so với mặt đất bao nhiêu mét?
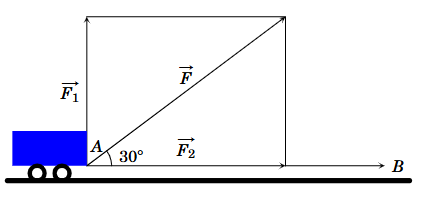
Một xe goòng được kéo bởi một lực \(\overrightarrow F \) có độ lớn là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài 200 m. Cho biết góc giữa \(\overrightarrow F \) và \(\overrightarrow {AB} \) là 30° và \(\overrightarrow F \) được phân tích thành hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (tham khảo hình vẽ). Tính công sinh bởi lực \(\overrightarrow {{F_1}} \) (đơn vị J).