Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 9
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau. Tìm đường tiệm cận ngang của đồ thị hàm số đó
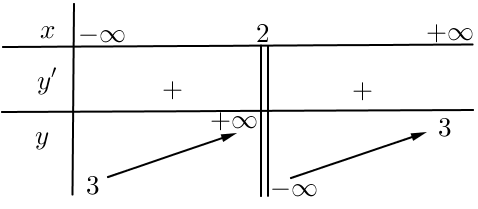
\(x = 2.\)
\(x = 3.\)
\(y = 2.\)
\(y = 3.\)
Hàm số \[y = \frac{x}{{{x^2} + 1}}\] đồng biến trên khoảng nào sau đây?
\[\left( { - \infty ;\, - 1} \right)\].
\[\left( { - 1;\,1} \right)\].
\[\left( { - \infty ;\, + \infty } \right)\].
\[\left( {0;\, + \infty } \right)\].
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 6x + 4y - 8z + 4 = 0\). Tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \(\left( S \right)\) lần lượt là
\(I\left( { - 3\,;\,2\,;\, - 4} \right)\), \(R = 5\).
\(I\left( {3\,;\, - 2;\,4} \right)\), \(R = 5\).
\(I\left( { - 3\,;\,2\,;\, - 4} \right)\), \(R = 25\).
\(I\left( { - 3\,;\,2\,;\, - 4} \right)\), \(R = 25\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị như hình vẽ bên.
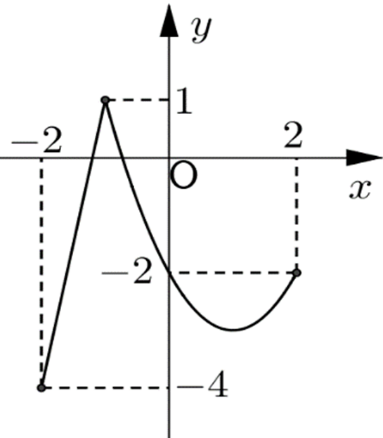
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) bằng
\( - 3.\)
\( - 4.\)
\(5.\)
\( - 5.\)
Trong không gian với hệ toạ độ Oxyz, cho điểm \(M\left( {2; - 1;5} \right)\), toạ độ hình chiếu vuông góc của điểm\(M\) lên trục \(Oy\) là
\(\left( {2;0;5} \right).\)
\(\left( {2; - 1;0} \right).\)
\(\left( {2; - 1;5} \right).\)
\(\left( {0; - 1;0} \right).\)
Trong không gian với hệ tọa độ \[{\rm{Ox}}yz\], cho hai vectơ \(\overrightarrow a = \left( {2; - 3;1} \right)\) và \(\overrightarrow b = \left( { - 1;4; - 2} \right)\). Giá trị của biểu thức \(\overrightarrow a .\overrightarrow b \) bằng
\(4\).
\( - 16\).
\( - 4\).
\(16\).
Cho ba điểm \[A\left( {1;0; - 2} \right),{\rm{ }}B\left( {2;1; - 1} \right),{\rm{ }}C\left( {1; - 2;2} \right)\] và điểm \(E\) là đỉnh thứ tư của hình bình hành \(ABCE\) thì tọa độ của \(E\) là
\(\left( {2; - 3;1} \right)\).
\(\left( {0; - 1;3} \right)\).
\(\left( {2; - 1 - 3} \right)\).
\(\left( {0; - 3;1} \right)\).
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Tìm giá trị của \(k\)thích hợp điền vào đẳng thức vectơ: \(\overrightarrow {AB} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {D{D_1}} = k\overrightarrow {A{C_1}} \)
\(k = 4\).
\(k = 2\).
\(k = 1\).
\(k = 0\).
Có một giá trị \({m_0}\) của tham số \(m\) để hàm số \(y = {x^3} + \left( {{m^2} + 1} \right)x + m + 1\) đạt giá trị nhỏ nhất bằng \(5\) trên đoạn \(\left[ {0;1} \right]\). Mệnh đề nào sau đây là đúng?
\(2{m_0} + 1 < 0\).
\(6{m_0} - m_0^2 < 0\).
\(2018{m_0} - m_0^2 \ge 0\).
\(2{m_0} - 1 < 0\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\)có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?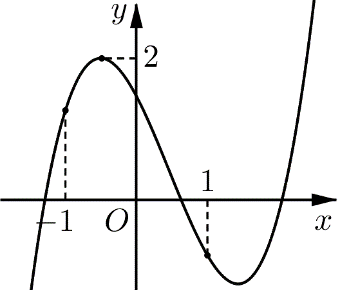
\(a > 0,{\rm{ }}b < 0,{\rm{ }}c < 0,{\rm{ }}d > 0.\)
\(a > 0,{\rm{ }}b > 0,{\rm{ }}c < 0,{\rm{ }}d > 0.\)
\(a > 0,{\rm{ }}b > 0,{\rm{ }}c > 0,{\rm{ }}d < 0.\)
\(a < 0,{\rm{ }}b < 0,{\rm{ }}c < 0,{\rm{ }}d < 0.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) là \(f'\left( x \right) = \left( {2x + 1} \right)\left( {x - 3} \right){\left( {x + 5} \right)^4}\). Hàm số đã cho có tất cả bao nhiêu điểm cực trị?
\(4\).
\(2\).
\(3\).
\(1\).
Biết đồ thị \(\left( {{C_m}} \right)\)của hàm số \(y = {x^4} - m{x^2} + m + 2018\)luôn luôn đi qua hai điểm \(M\)và \(N\)cố định khi \(m\)thay đổi. Tọa độ trung điểm \(I\)của đoạn thẳng \(MN\)là
\(I\left( {0;\,1} \right)\).
\(I\left( {0;\,2018} \right)\).
\(I\left( {1;\,2018} \right)\).
\(I\left( {0;\,2019} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - m{x^2} + \left( {4\;m - 2} \right)x + 1 - 4\;m}}{{x - 1}}\) có đồ thị là \(\left( C \right)\) với \(m\) là tham số
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\).
c) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\).
d) Có 2 phương trình tiếp tuyến của \(\left( C \right)\) song song với đường thẳng \(x - y = 0\).
Cho hàm số \(y = \frac{{ - m{x^2} + (4\;m - 2)x + 1 - 4\;m}}{{x - 1}}\)
a) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\)
b) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị
c) Có 2 phương trình tiếp tuyến của \((C)\) song song với đường thẳng \(x - y = 0\)
d) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\)
Cho hàm số \(y = \left( {{m^2} - 1} \right){x^3} + \left( {m - 1} \right){x^2} - x + 4\) . Khi đó
a) Khi \(m = 1\) thì hàm số đồng biến trên khoảng \(\left( { - \infty \,; + \infty } \right)\).
b) Khi \(m = 0\) thì hàm số nghịch biến trên khoảng \(\left( { - \infty \,; + \infty } \right)\).
c) Khi \(m = 3\) thì hàm số đồng biến trên khoảng \(\left( {3\,; + \infty } \right)\).
d) Tổng các giá trị nguyên của tham số \(m\) để hàm số \(y = \left( {{m^2} - 1} \right){x^3} + \left( {m - 1} \right){x^2} - x + 4\) nghịch biến trên khoảng\(\left( { - \infty \,; + \infty } \right)\) bằng 2.
Nồng độ thuốc \(C\left( t \right)\) tính theo \({\rm{mg}}/{\rm{c}}{{\rm{m}}^3}\) trong máu của bệnh nhân được tính bởi \(C\left( t \right) = \frac{{0,05t}}{{{t^2} + t + 1}}\), trong đó \(t\) là thời gian tính theo giờ kể từ khi tiêm cho bệnh nhân.
a) Hàm số \(C\left( t \right)\) có đạo hàm \(C'\left( t \right) = \frac{{1 - {t^2}}}{{20{{\left( {{t^2} + t + 1} \right)}^2}}},t \ge 0\).
b) Sau khi tiêm, nồng độ thuốc trong máu của bệnh nhân giảm dần theo thời gian.
c) Nồng độ thuốc trong máu lớn nhất ở thời điểm 1 giờ sau khi tiêm.
d) Có thời điểm nồng độ trong máu của bệnh nhân đạt \(0,02{\rm{mg}}/{\rm{c}}{{\rm{m}}^3}\).
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kể với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC,SD sao cho S.ABCD là hình chóp tứ giác đều có góc ASC = 60° . Biết P= =m.g, trong đó g là vectơ gia tốc rơi tự do có độ lớn 10 m/s, P là trọng lực tác động lên vật có đơn vị là N, m là khối lượng của vật có đơn vị kg. Độ lớn của lực căng cho mỗi sợi xích bằng bao nhiêu Niu-tơn ?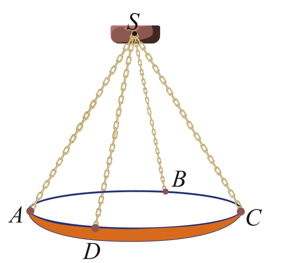
Một toà nhà được thiết kế để làm 2 phòng dạy học có trang bị máy chiếu. Mái nhà là dạng mái vát \(CDFE\) như hình vẽ. Chiều dài của mỗi phòng học là \(OA = 30m\) và chiều rộng là \(OB = 20m\), chiều cao các bức tường \(BD = 10m\) và \(EA = 6m\). Từ vị trí \(P\) cách \(B\) một khoảng 10 m, người ta xây các bậc thang cao dần về phía cuối của phòng học để đặt các dãy bàn ghế học sinh trên các bậc thang đó. Chiều rộng mỗi bậc thang là 2 m và chiều cao mỗi bậc thang là 20 cm.
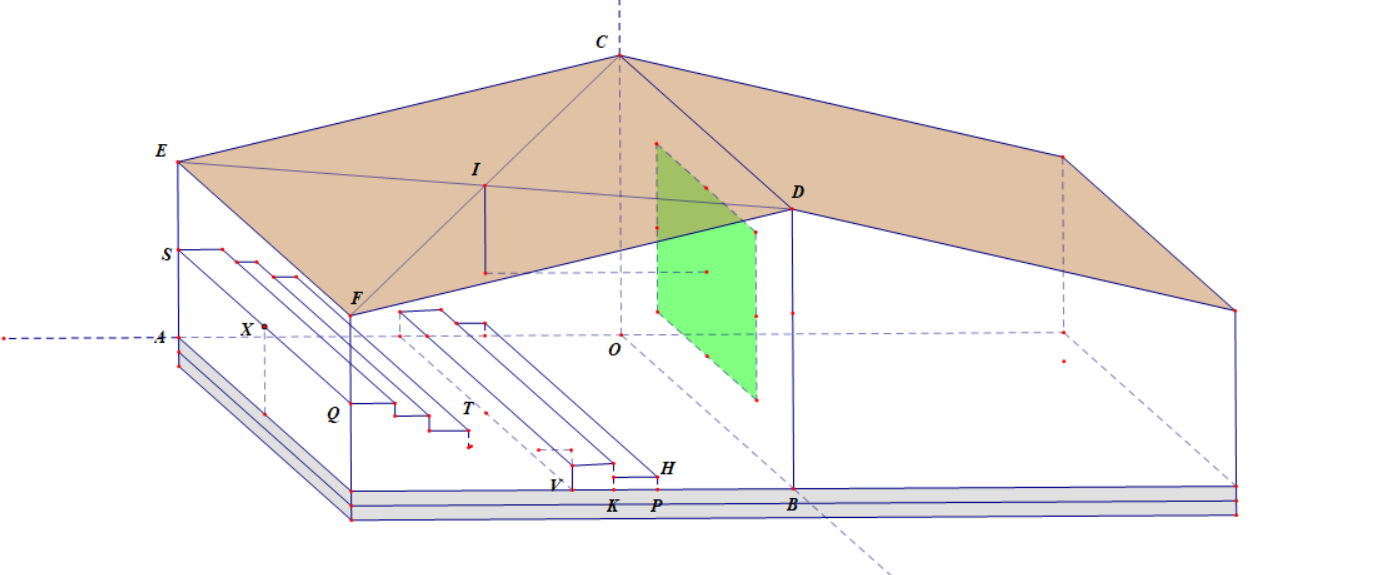
Chủ toà nhà muốn lắp giá treo máy chiếu tại vị trí \(I\) là giao của \(DE\) và \(CF\) như hình vẽ, vuông góc với mặt sàn sao cho không vướng vào đầu học sinh khi học sinh đó đứng tại bậc thang ngay dưới máy chiếu và cũng không che khuất tầm nhìn của học sinh ngồi ở hàng ghế sau cùng, tại vị trí \(X\) trung điểm \(SQ\), theo phương vuông góc bức tường \(OBDC\). Hỏi tổng độ dài thanh treo máy chiếu và cả thân máy chiếu lớn nhất là bao nhiêu mét? Kết quả làm tròn đến hàng phần mười.
Khi làm nhà kho, bác Cường muốn để cửa sổ có dạng hình chữ nhật với diện tích bằng \(3,4{\mkern 1mu} {{\rm{m}}^2}\) . Tìm chu vi nhỏ nhất của khung cửa sổ ?

Quan sát một đàn ong trong 20 tuần, người ta ước lượng được số lượng ong trong đàn bởi công thức \(P\left( t \right) = \frac{{20000}}{{1 + 1000{e^{ - t}}}}\), trong đó \(t\) là thời gian tính theo tuần kể từ khi bắt đầu quan sát, \(0 \le t \le 20\). Tại thời điểm nào thì số lượng ong của đàn tăng nhanh nhất ?
Vận tốc trung bình của dòng xe trên đoạn đường 124 từ 6#A.M. đến 10#A.M. được xấp xỉ bởi \(f(t) = 20t - 40\sqrt t + 50,\quad 0 \le t \le 4\) trong đó \(t\) tính bằng giờ kể từ \(6\;\)A.M. và \(f(t)\) tính bằng km/giờ. Hỏi vào thời điểm mấy giờ trong buổi sáng thì vận tốc trung bình thấp nhất?
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G\left( x \right) = 0,035{x^2}\left( {15 - x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.








