Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 8
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian với hệ toạ độ Oxyz, cho điểm \(M\left( {2;1; - 3} \right)\). Khoảng cách từ \(M\) đến gốc toạ độ \(O\) bằng:
\(\sqrt 5 .\)
\(\sqrt {14} .\)
\(0.\)
\(\sqrt {10} .\)
Trong không gian Oxyz, hình chiếu vuông góc của điểm \(M(2;1; - 1)\) trên mặt phẳng (Ozx)có tọa độ là
\[\left( {2\,;\,0\,;\, - 1} \right)\].
\[\left( {2\,;\,1\,;\,0} \right)\].
\[\left( {0;\,1\,;\, - 1} \right)\].
\[\left( {0\,;\,1\,;\,0} \right)\].
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow u = \left( {1\,;\, - 2\,;\,1} \right)\) và \(\overrightarrow v = \left( {2\,;\,1\,;\, - 1} \right)\). Vectơ nào dưới đây vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \)?
\(\overrightarrow {{w_2}} = \left( { - 1\,;\,3\,;\,5} \right)\).
\(\overrightarrow {{w_4}} = \left( {1\,;\,4\,;\,7} \right)\).
\(\overrightarrow {{w_1}} = \left( { - 2\,;\, - 6\,;\, - 10} \right)\).
\(\overrightarrow {{w_3}} = \left( {1\,;\, - 4\,;\,7} \right)\).
Hàm số \(y = {x^3} + 3{x^2}\) nghịch biến trên khoảng nào sau đây?
\(\left( {0;4} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - 2;0} \right)\).
\(\left( { - \infty ; - 2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới. Số đường tiệm cận ngang của đồ thị hàm số đã cho là
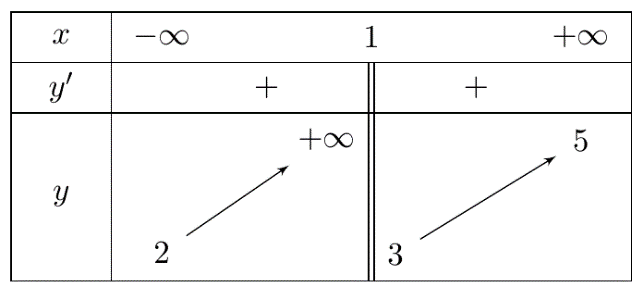
\(1\).
\(3\).
\(4\).
\[2\].
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2\,;\,2} \right]\).
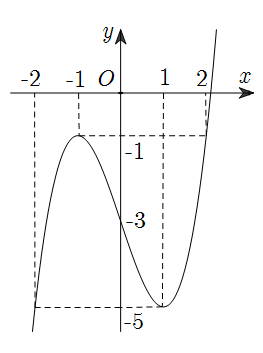
\(m = - 1\,;\,M = 0\).
\(m = - 5\,;\,M = 0\).
\(m = - 5\,;\,M = - 1\).
\(m = - 2\,;\,M = 2\).
Trong không gian với hệ tọa độ Oxyz cho ba điểm \[M\left( {1;\,1;\,1} \right)\], \[N\left( {2;\,3;\,4} \right)\],\[P\left( {7;\,7;\,5} \right)\]. Để tứ giác \[MNPQ\] là hình bình hành thì tọa độ điểm \[Q\] là
\[\left( {6;\,5;\,2} \right)\].
\[\left( { - 6;\,5;\,2} \right)\].
\[\left( {6;\, - 5;\,2} \right)\].
\[\left( { - 6;\, - 5;\, - 2} \right)\].
Số điểm có tọa độ nguyên thuộc đồ thị hàm số \(y = \frac{{2{{\rm{x}}^2} + 3{\rm{x}} + 10}}{{x + 2}}\)là
\(10\).
\(16\).
\(12\).
\(8\).
Cho ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]không đồng phẳng. Xét các vectơ \[\overrightarrow x = 2\overrightarrow a - \overrightarrow b ;\overrightarrow y = - 4\overrightarrow a + 2\overrightarrow b ;\overrightarrow z = - 3\overrightarrow b - 2\overrightarrow c \]. Chọn khẳng định đúng?
Hai vectơ\[\overrightarrow x ;\overrightarrow y \]không cùng phương.
Hai vectơ\[\overrightarrow x ;\overrightarrow z \]cùng phương.
Ba vectơ\[\overrightarrow x ;\overrightarrow y ;\overrightarrow z \]đồng phẳng.
Hai vectơ\[\overrightarrow y ;\overrightarrow z \]cùng phương.
Cho hàm số \[y = f\left( x \right)\] có đồ thị \[y = f'\left( x \right)\] của nó trên khoảng \[K\] như hình vẽ. Khi đó trên \[K\] hàm số \[y = f\left( {x - 2019} \right)\] có bao nhiêu điểm cực trị?
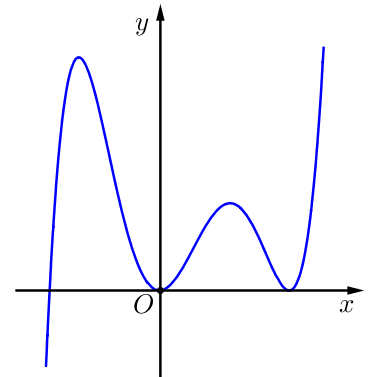
\[2\].
\[1\].
\[3\].
\[4\].
Cho hàm số \(y = {x^2} - 6x + m\) (\(m\) là tham số thực) thỏa mãn \[\mathop {\min }\limits_{\left[ {0;4} \right]} y + \mathop {\max }\limits_{\left[ {0;4} \right]} y = - 23\]. Mệnh đề nào sau đây đúng?
\(m < - 10\).
\(0 < m < 10\).
\( - 7 < m < 0\).
\( - 10 < m \le - 7\).
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + 3\,\left( {a \ne 0} \right)\) có bảng biến thiên như sau: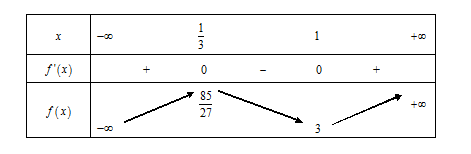
Xác định dấu của hệ số \(a,b,c\).
\(a > 0,b < 0,c > 0\).
\(a < 0.b < 0,c < 0\).
\(a > 0,b > 0,c > 0\).
\(a < 0,b < 0,c > 0\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị là đường cong \((C)\).
a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
b) Để phương trình \({x^2} + 3x + 3 = m|x + 2|\) có 4 nghiệm phân biệt thì \(m > 2\).
c) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến với \((C)\) vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2},\frac{3}{2}} \right)\).
Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x)\) xác định và liên tục trên \(\mathbb{R}\) và \(f'(x)\) có đồ thị như hình vẽ dưới đây:
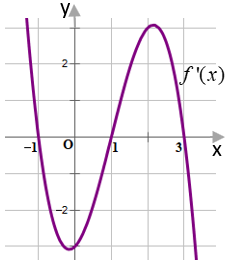
Xét tính đúng sai của các khẳng định sau:
a) \[\mathop {Max}\limits_{(1; + \infty )} f(x) = f(2)\].
b) Hàm số \(y = f(3 - 2x)\) đồng biến trên khoảng \(( - \infty ;0)\).
c) Hàm số\(y = f(x)\) có hai điểm cực trị.
d) \(f'(x) < 0\,\,\forall \,x \in ( - 1;1)\).
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \(30.000\) đồng mà cứ tăng giá thêm \(1000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\). Hỏi:
a) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần tăng thêm \[10000\] đồng?
b) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá \[39000\] đồng?
c) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi chiếc khăn lãi \[21000\] đồng?
d) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm \[800\] chiếc?
Cho tứ diện \(ABCD\) với \(A\left( {2;1;0} \right),B\left( {1;1;3} \right),C\left( {2; - 1;3} \right),D\left( {1; - 1;0} \right)\).
a) Khoảng cách giữa 2 đường thẳng \(AB\) và \(CD\) bằng \(3\)
b) Tứ diện \(ABCD\) có các cạnh đối đôi một bằng nhau.
c) Góc giữa 2 đường thẳng \(AB\) và \(CD\) là \(\varphi = \arccos 0,3\)
d) Bán kính của mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(\frac{{\sqrt {14} }}{2}\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho biết máy bay \(A\) đang bay với vectơ vận tốc \(\vec a = \left( {300;200;400} \right)\) (đơn vị: km/h). Máy bay \(B\) bay cùng hướng và có tốc độ gấp ba lần tốc độ của máy bay \(A\). (làm tròn đến hàng đơn vị)

Tính tốc độ của máy bay \(B\).
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả hàm số :
\(y = h\left( x \right) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840;\left( {0 \le x \le 2000} \right)\)
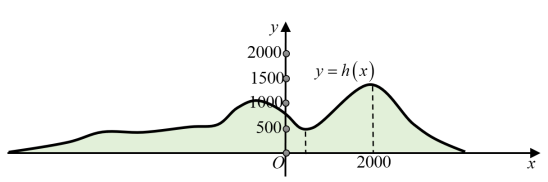
Trên đoạn \(\left[ {0;2000} \right]\) cưa lát cắt dãy núi nơi thấp nhất có hoành độ bao nhiêu ?
Giả sử tăng cân nặng ( tính bằng \(kg\)) của một giống vật nuôi ( trong vòng một số tháng nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số: \(f\left( t \right) = \frac{{150}}{{1 + 3{e^{ - t}}}},\;\;t \ge 0\)
Trong đó thời gian \(t\) được tính bằng tháng kể từ khi vật nuôi đó bắt đầu sinh ra. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ tăng cân nặng của loài cây đó. Hỏi sau khi vật nuôi sinh ra thì sau bao nhiêu tháng tốc độ tăng cân nặng của vật nuôi là nhanh nhất?
Một công ty bất động sản có \(20\) phòng cho thuê. Biết rằng nếu cho thuê mỗi phòng với giá \(2\) triệu đồng một tháng thì tất cả các phòng đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi phòng thêm \(200\) nghìn đồng một tháng thì có thêm một phòng bị bỏ trống. Hỏi công ty nên cho thuê mỗi phòng bao nhiêu triệu đồng một tháng để tổng số tiền thu được là lớn nhất?
Một em bé cân nặng \(m = 20{\rm{\;kg}}\) trượt trên cầu thang trượt dài 2 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \({40^ \circ }\). Cho biết công \(A\left( J \right)\) sinh bởi một lực \(\vec F\) có độ dịch chuyển \(\vec d\) được tính theo công thức \(\vec A = \vec F \cdot \vec d\). Hãy tính công sinh bởi trọng lực \(\vec P\) khi em bé trượt hết chiều dài cầu trượt biết \(g \approx 10{\rm{\;m}}/{{\rm{s}}^2}\). (làm tròn đến hàng đơn vị).
Một vật chuyển động theo quy luật \(s = - \frac{1}{2}{t^3} + 6{t^2}\) với \(t\) là khoảng thời gian tính từ khi vật đó bắt đầu chuyển động và \(s\left( {\rm{m}} \right)\) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian \(6\) giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bào nhiêu?








