Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 7
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các khẳng định sau, khẳng định nào sai ?
\[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\cos \left( {\vec u,\,\vec v} \right)\].
\[\left[ {\vec u,\vec v} \right] = \vec 0\] \[ \Leftrightarrow \]\[\vec u\], \[\vec v\] cùng phương.
Nếu \[\vec u\], \[\vec v\] không cùng phương thì giá của vectơ \[\left[ {\vec u,\vec v} \right]\] vuông góc với mọi mặt phẳng song song với giá của các vectơ \[\vec u\] và \[\,\vec v\].
\[\left[ {\vec u,\vec v} \right].\,\vec u = \left[ {\vec u,\vec v} \right].\,\vec v = \vec 0\].
Trong không gian với hệ tọa độ Oxyz, cho vectơ \(\overrightarrow u = \left( {x;2;1} \right)\)và \(\overrightarrow v = \left( {1; - 1;2x} \right)\). Tính tích vô hướng của \(\overrightarrow u \)và \(\overrightarrow v \).
\(x + 2\).
\(3x - 2\).
\(3x + 2\).
\( - 2 - x\)
Tìm tọa độ điểm \(M'\) là điểm đối xứng của điểm \(M\left( {1;2;3} \right)\) qua gốc tọa độ \(O\).
\(M'\left( { - 1;2;3} \right)\).
\(M'\left( { - 1; - 2; - 3} \right)\).
\(M'\left( {1;2; - 3} \right)\).
\(M'\left( { - 1; - 2;3} \right)\).
Cho hàm số \[y = \frac{{x + 1}}{{2 - x}}\]. Khẳng định nào sau đây đúng?
Hàm số đã cho đồng biến trên từng khoảng xác định của nó.
Hàm số đã cho đồng biến trên khoảng \[\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right)\].
Hàm số đã cho nghịch biến trên \[\mathbb{R}\].
Hàm số đã cho nghịch biến trên từng khoảng xác định của nó.
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 1}}{{x - 2}}\) là
\(y = 1\).
\(y = 2\).
\(x = 2\).
\(x = 1\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\). Giá trị \(M + m\) bằng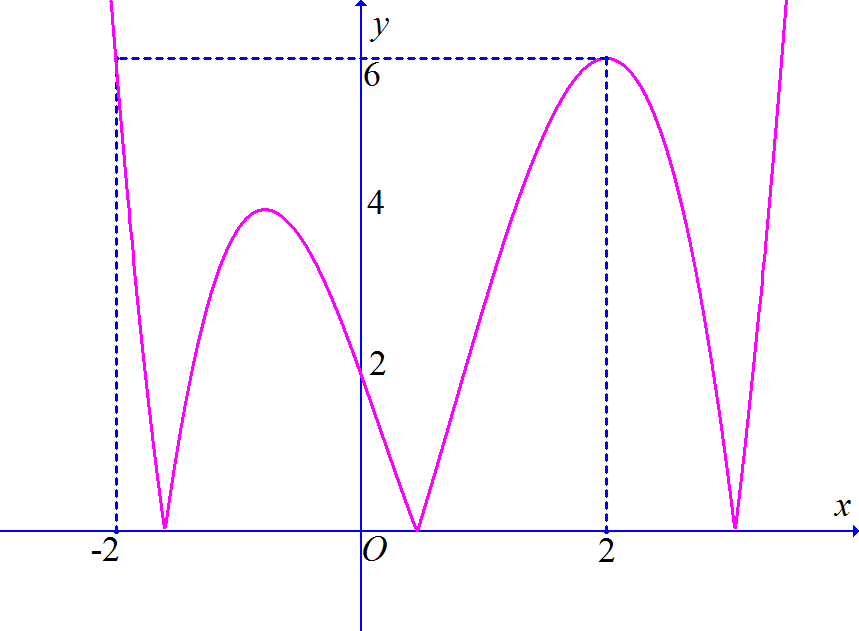
8.
9.
6.
4.
Bảng biến thiên sau là của hàm số nào?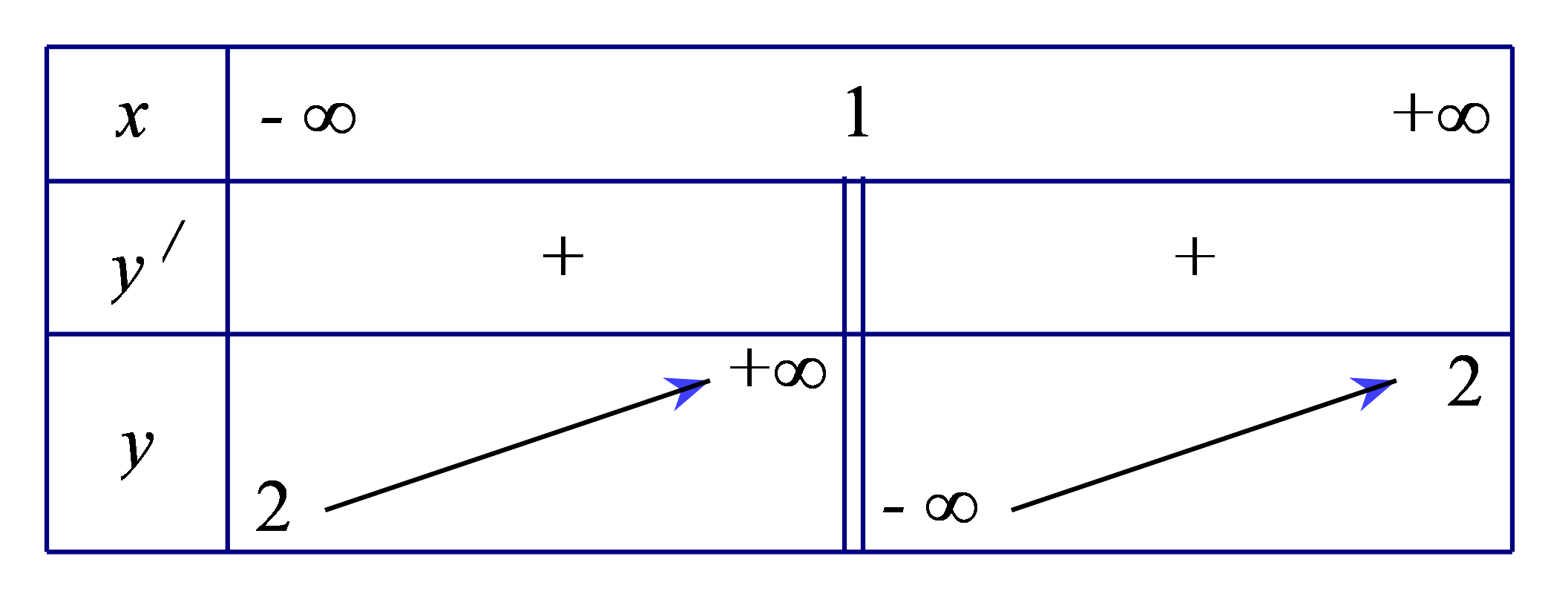
\(y = \frac{{ - 2x + 3}}{{1 - x}}\).
\(y = \frac{{x + 5}}{{x - 2}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{x - 6}}{{x - 2}}\).
Cho hàm số \(y = \frac{{ax - b}}{{x - 1}}\) có đồ thị như hình dưới đây.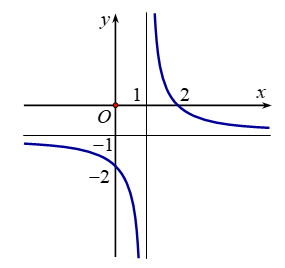
Khẳng định nào dưới đây là đúng?
\(0 < a < b\).
\(0 < b < a\).
\(b < 0 < a\).
\(b < a < 0\).
Cho hàm số \[y{\rm{ }} = {\rm{ }}f\left( x \right)\] có đạo hàm \(f'(x) = x{(x + 3)^2},\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(2\).
\(3\).
\(1\).
\(0\).
Cho hàm số \(y = \frac{{x - {m^2}}}{{x + 8}}\) với \(m\) là tham số thực. Giả sử \({m_0}\) là giá trị dương của tham số \(m\) để hàm số có giá trị nhỏ nhất trên đoạn \(\left[ {0;3} \right]\) bằng 3. Giá trị \({m_0}\) thuộc khoảng nào trong các khoảng cho dưới đây?
\(\left( {20;25} \right)\).
\(\left( {2;5} \right)\).
\(\left( {6;9} \right)\).
\(\left( {1;4} \right)\).
Cho tứ diện \[ABCD\]. Đặt \[\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c ,\]gọi G là trọng tâm của tam giác \[BCD\]. Trong các đẳng thức sau, đẳng thức nào đúng?
\[\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
\[\overrightarrow {AG} = \frac{1}{2}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
\[\overrightarrow {AG} = \overrightarrow a + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
Trong không gian với hệ tọa độ Oxyz cho tam giác \(ABC\) có \(A\left( {1\,;\,3\,;\,5} \right)\,,{\rm{ }}B\left( {2\,;\,0\,;\,1} \right)\) và \(G\left( {1\,;\,4\,;\,2} \right)\)là trọng tâm. Tìm tọa độ điểm \(C.\)
\(C\left( {0\,;\, - 9\,;\,0} \right)\).
\(C\left( {\frac{4}{3}\,;\,\frac{7}{3}\,;\,\frac{8}{3}} \right)\).
\(C\left( {0\,;\,0\,;\,9} \right)\).
\(C\left( {0\,;\,9\,;\,0} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \[y = \left( {m - 1} \right){x^4} - 2\left( {m - 3} \right){x^2} + 1\](\(m\) là tham số). Khi đó:
a) Nếu \(m = 1\) thì hàm số không có cực đại
b) Nếu \(m = 2\) thì hàm số có 1 điểm cực trị
c) Nếu \(m = 0\) thì điểm cực tiểu của đồ thị hàm số là \(M\left( {a;b} \right)\) khi đó \(ab = 1\)
d) Để hàm số \[y = \left( {m - 1} \right){x^4} - 2\left( {m - 3} \right){x^2} + 1\] không có cực đại thì \(m \in \left[ {a;b} \right]\) khi đó \(a + b = 3\)
Trong không gian Oxyz, cho điểm \[A\left( { - 2\,;3\,;1} \right)\], \[B\left( {5\,;\, - 3\,;\,2} \right)\] và \(C( - 2\,;\,2\,;\,4)\). Đường thẳng \[AB\]cắt mặt phẳng \[\left( {Oyz} \right)\] tại điểm \[M\].
a) Tọa độ của điểm \(M\) là \(\left( {0\,;\,\frac{9}{7}\,;\,\frac{9}{7}} \right)\).
b) Tam giác \(ABC\) vuông tại \(A\).
c) \(\overrightarrow {AB} = \left( { - 7\,;\, - 6\,;\,1} \right)\).
d) Tọa độ trọng tâm của tam giác \(ABC\) là \(G\left( {\frac{1}{3}\,;\,\frac{2}{3}\,;\,\frac{7}{3}} \right)\).
Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá \[2\,000\,000\,\]đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm \[50\,000\] đồng một tháng thì có thêm một căn hộ bị bỏ trống. Hỏi :
a) Thu nhập cao nhất công ty có thể đạt được trong 1 tháng là \[101250000\]đồng?
b) Thu nhập cao nhất công ty có thể đạt được trong 1 tháng là \[105250000\]đồng?
c) Có 5 căn hộ bị bỏ trống thì công ty có thu nhập cao nhất ?
d) Để công ty có thu nhập cao nhất trong 1 tháng thì giá cho thuê là \[2500000\]đồng?
Cho hàm số \[y = \frac{{{x^2} + x - 5}}{{x - 2}}\] có đồ thị \((C)\).
a) Tập xác định:\[D = \mathbb{R}\backslash \left\{ 2 \right\}\].
b) Đường thẳng \(x = 2\)là tiệm cận đứng của \((C)\).
c) Đường thẳng \(y = x + 3\) là tiệm cận xiên của \((C)\).
d) Hàm số đồng biến trên các khoảng (\( - \infty ;1)\)và (\(3; + \infty )\). Hàm số nghịch biến trên các khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một bể ban đầu chứa 10 gal dung dịch muối với 2 lb muối. Dung dịch vào có nồng độ \(1.5lb/gal\) chảy vào với tốc độ \(3gal/\) phút, và hỗn hợp trong bể chảy ra với tốc độ \(4gal/\) phút. Người ta cho biết lượng muối trong bể sau \(t\) phút là \(x\) (pound), với\(x = f(t) = 1,5(10 - t) - 0,0013{(10 - t)^4},\quad 0 \le t \le 10.\)Hỏi lượng muối tối đa có thể có trong bể tại một thời điểm nào đó là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
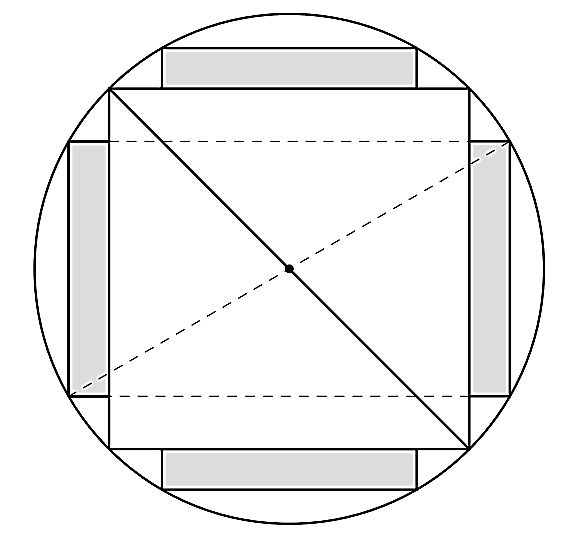
Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm, cần xả thành một chiếc xà có tiết diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng \(x\) của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. (làm tròn kết quả đến hàng phần trăm).
Một doanh nghiệp dự định sản xuất \(200\) máy tính bảng dành cho học sinh. Nếu doanh nghiệp đó bán \(x\) máy tính bảng \(\left( {1 \le x \le 200,x \in \mathbb{N}} \right)\) thì giá bán cho mỗi máy tính bảng là \(p\left( x \right) = 4000 - 10x\)(nghìn đồng), trong đó chí phí để sản xuất mỗi máy tính bảng là \(c\left( x \right) = {x^2} - 70x + 400 + \frac{{1000}}{x}\)(nghìn đồng). Hỏi doanh nghiệp đó sẽ bán bao nhiêu máy tính bảng để lợi nhuận cao nhất?.
Một em nhỏ cân nặng \(m = 25\;\)kg trượt trên cầu trượt dài \(3,5\;\)m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ \).
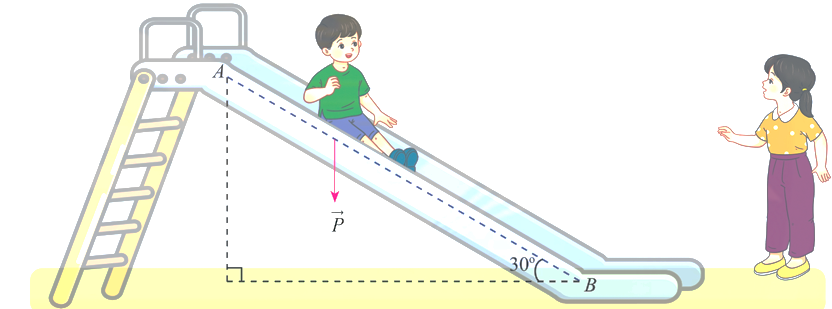
Tính độ lớn của trọng lực \(\vec P = m\vec g\) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\vec g\) có độ lớn là \(g = 9,8\;{\rm{m/}}{{\rm{s}}^2}\). (làm tròn đến hàng đơn vị)
Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết \[a = 24\] và \[b = 3\], Biết chiều dài tối thiểu của que sào thỏa mãn điều kiện trên là \(l\). Tính giá trị của \({l^2}\).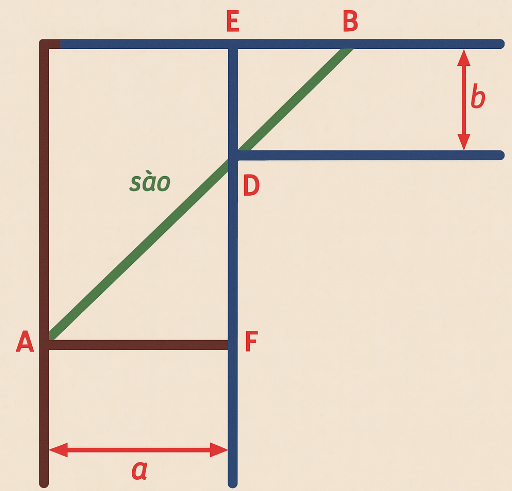
Trong không gian với hệ tọa độ Oxyz (đơn vị đo lấy theo \(km\)), một Radar phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm \(A\left( {812;\,600\,;\,5} \right)\) đến điểm \(B\left( {950\,;\,530\,;\,6} \right)\) trong 10 phút.
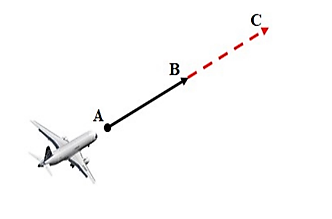
Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là \(C\left( {x;\,y\,;\,z} \right)\). Khi đó \(x + y + z\) bằng bao nhiêu?
