Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 6
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow x = \overrightarrow i - 3\overrightarrow j + 2\overrightarrow k \). Tìm tọa độ của \(\overrightarrow x \)
\[\overrightarrow x = \left( {1; - 3;2} \right)\].
\[\overrightarrow x = \left( { - 1; - 3;2} \right)\].
\[\overrightarrow x = \left( {1; - 3;0} \right)\].
\[\overrightarrow x = \left( { - 1;3; - 2} \right)\].
Hàm số \(y = f\left( x \right)\)liên tục và có bảng biến thiên như hình bên. Gọi \[M\]là giá trị lớn nhất của hàm số \[y = f\left( x \right)\]trên nữa khoảng \[\left[ {0;3} \right)\]. Tìm mệnh đề đúng.![Chọn AD. \[M = f\left( 5 \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/12-1761615261.png)
\[M = f\left( 0 \right)\].
\[M = f\left( 2 \right)\].
\[M = f\left( 3 \right)\].
\[M = f\left( 5 \right)\].
Trong không gian với hệ trục tọa độ Oxyz, cho hai véc tơ \(\overrightarrow u = \left( {2;3;0} \right),\overrightarrow v = \left( {1; - 1;4} \right)\). Tích vô hướng của hai véc tơ đó bằng:
1
0
\( - 1\)
2
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} - 6x + 4y - 8z + 4 = 0.\] Toạ độ tâm \[I\]của mặt cầu \[\left( S \right)\] là
\[\left( { - 3;\,2;\,4} \right)\].
\[\left( {3;\, - 2;\,4} \right)\].
\[\left( {3;\, - 2;\, - 4} \right)\].
\[\left( { - 3;\,2;\, - 4} \right)\].
Hàm số \(y = f\left( x \right)\) bảng biến thiên như hình bên. Khẳng định nào sau đây sai?
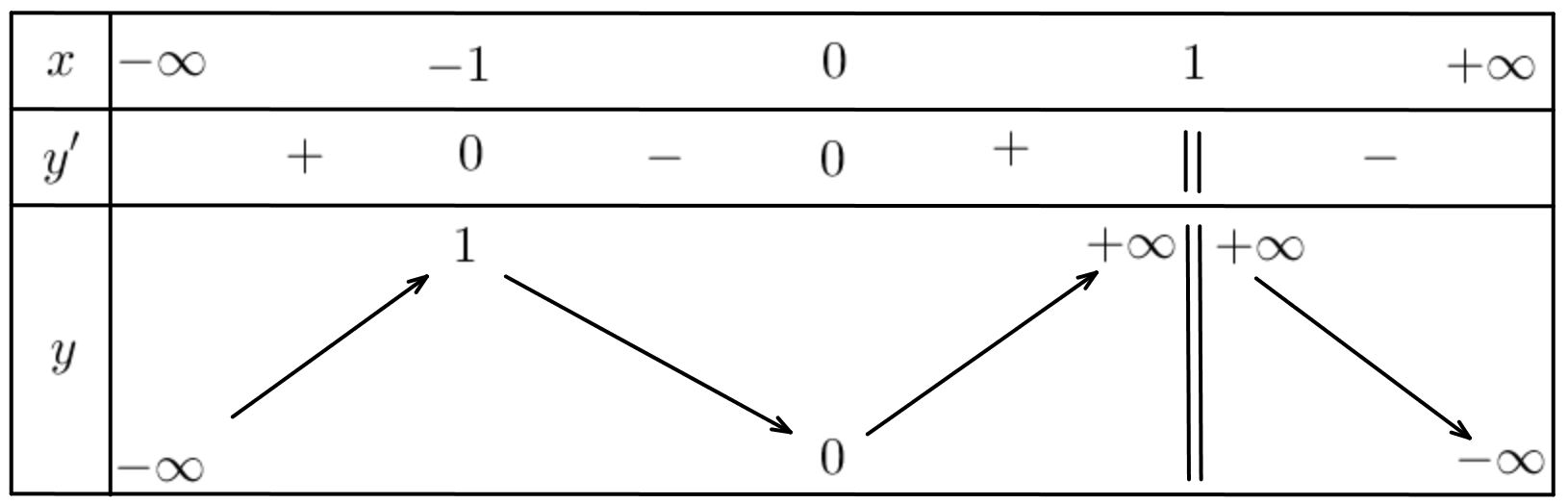
Hàm số có hai cực trị.
Đồ thị hàm số có 1 đường tiệm cận.
Hàm số nghịch biến trên khoảng \(\left( {1\,;\, + \infty } \right)\).
Hàm số có hai điểm cực đại.
Các khoảng nghịch biến của hàm số \(y = {x^3} - 12x + 12\) là:
\(\left( { - \infty ; - 2} \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( { - 2;2} \right)\).
\(\left( { - \infty ; - 2} \right)\,;\,\left( {2; + \infty } \right)\).
Cho hàm số \(f\left( x \right) = \frac{{x - m}}{{x + 4}}\). Tổng tất cả các giá trị của \(m\) để \(\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 2\) là
\(\frac{1}{2}\).
\(0\).
\( - 11\).
\(1\).
Cho hàm số \(f(x) = \frac{{2 - ax}}{{bx - c}}\)\(\left( {a,b,c \in \mathbb{R}} \right)\)có bảng biến thiên như sau:
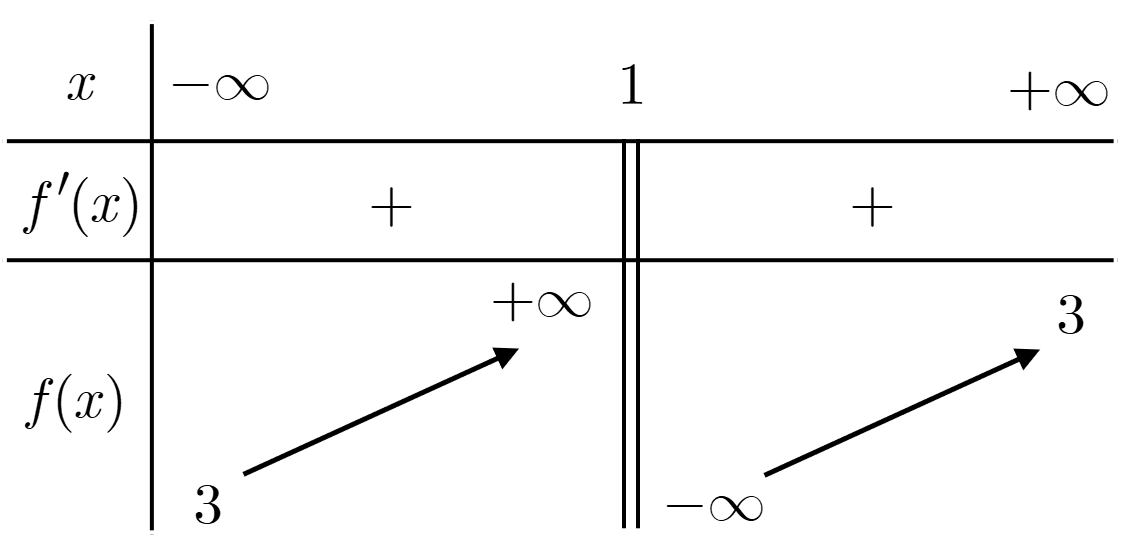
Tổng các số \(a + b + c\)thuộc khoảng nào sau đây
\(\left( { - 2;0} \right)\).
\(\left( { - \frac{2}{3};0} \right)\).
\(\left( {0;\frac{2}{3}} \right)\).
\(\left( {0;2} \right)\).
Cho tứ diện đều \(ABCD\) . Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} \) bằng
\(\frac{{{a^2}}}{2}\).
\( - \frac{{{a^2}}}{2}\).
\({a^2}\).
\(0\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {1 - x} \right)^2}{\left( {3 - x} \right)^3}{\left( {x - 2} \right)^4}\) với mọi \(x \in \mathbb{R}\). Điểm cực tiểu của hàm số là
\(x = 3\).
\(x = 2\).
\(x = 0\).
\(x = 1\).
Đồ thị hàm số \[y = \frac{{2x + 1}}{{3 - x}}\] có tâm đối xứng là
\(I\left( {3;2} \right)\).
\(I\left( {3; - 2} \right)\).
\(I\left( {3; - 1} \right)\).
\(I\left( { - 2;3} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow {OA} = 3\overrightarrow i + \overrightarrow j - 2\overrightarrow k \) và \(B\left( {m;m - 1; - 4} \right)\). Tìm tất cả giá trị của tham số \(m\)để độ dài đoạn \(AB = 3\).
\(m = 2\) hoặc \(m = 3\).
\(m = 1\) hoặc \(m = 2\) .
\(m = 1\) hoặc \(m = 4\).
\(m = 3\) hoặc \(m = 4\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một công ty bất động sản có \[150\] căn hộ cho thuê, biết rằng nếu cho thuê mỗi căn hộ với giá\[2\]triệu đồng mỗi tháng thì mỗi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm \[100.000\] đồng mỗi tháng thì có thêm \[5\] căn hộ bị bỏ trống. Mệnh đề nào sau đây đúng
a) Thu nhập cao nhất của công ty đạt được là 312.500.000 đồng.
b) Khi giá cho thuê mỗi căn hộ là 2.200.000 đồng thì có 10 căn hộ bị trống
c) Khi thu nhập công ty cao nhất thì số căn hộ có người thuê là 125 căn hộ.
d) Khi giá cho thuê mỗi căn hộ là 2.700.000 đồng thì thu nhập của công ty cao nhất.
Cho hàm số \(y = \left( {3{m^2} - 12} \right){x^3} + 3\left( {m - 2} \right){x^2} - x + 2\) (tham số \[m\]). Khi đó
a) Khi \(m = 0\) thì hàm số đồng biến trên \(\mathbb{R}\).
b) Khi \(m = \pm 2\) thì hàm số nghịch biến trên \(\mathbb{R}\).
c) Có 3 giá trị nguyên của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\).
d) Tổng bình phương của tất cả các giá trị nguyên của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\)là 5.
Trong hệ trục Oxyz, cho 3 điểm \(A\left( {1;0;0} \right),B\left( {0;0;1} \right),C\left( {2;1;1} \right)\). Xét tính đúng sai của các mệnh đề sau:
a) Diện tích của tam giác \(ABC\) bằng \(\frac{{\sqrt 6 }}{2}\)(đvdt)
b) Gọi \(D\left( {x;y;z} \right)\) sao cho tứ giác \(ABCD\) là một hình bình hành khi đó \(x + y + z = 3\)
c) Độ dài đường cao của tam giác \(ABC\) hạ từ \(A\) bằng \(AH = \frac{{\sqrt {30} }}{5}\)(đơn vị dài)
d) Thể tích của khối chóp \(SABCD\) với đỉnh \(S\left( {0;3;4} \right)\) bằng \(2\)(đvtt)
Cho hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\). Khi đó:
a) Tập xác định của hàm số là \(D = R\backslash \left\{ 1 \right\}\).
b) Đồ thị hàm số có hai điểm cực trị lần lượt là \(A(0;2),B( - 2; - 2).\)
c) Đồ thị hàm số có đường tiệm cận xiên là đường thẳng \(y = x - 1.\)
d) Hàm số có đồ thị như hình vẽ:
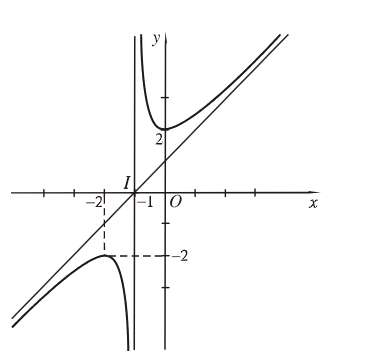
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty bất động sản có \[50\] căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá \[x\] triệu đồng mỗi tháng thì lợi nhuận của công ty sẽ được biểu diễn bởi hàm số \[F\left( x \right) = - \frac{{{x^2}}}{{50.000}} + 90x\] (đồng). Vậy công ty cần cho thuê căn hộ với giá bao nhiêu để lợi nhuận của công ty cao nhất?
Trong không gian, một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cầu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 60°. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết rằng các lực căng F1, F2, F3, F4 đều có cường độ là 4700N. Tìm ![]() (làm tròn kết quả đến hàng đơn vị của Niu-tơn))
(làm tròn kết quả đến hàng đơn vị của Niu-tơn))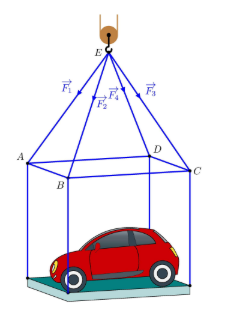
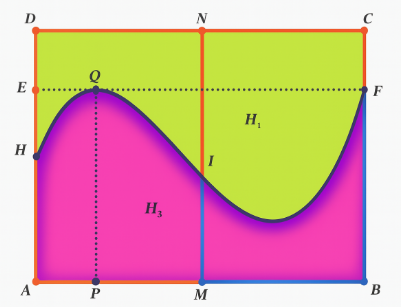
Khuôn viên của một công viên có dạng hình chữ nhật \[ABCD\]với \[AB = 100\;m;\;AD = 80\;m.\] Người ta muốn chia công viên thành hai khu, một khu dành cho trẻ em, một khu dành cho người lớn. Để tạo thiết kế độc đáo và lạ mắt, người ta dùng một đường cong chia khuôn viên thành hai phần \[{H_1}\] (không tô màu) dành cho trẻ em và \[{H_2}\] (tô màu) dành cho người lớn như hình vẽ bên với \[AH = 40\;m;\;AE = 60\;m;AP = 20\;m\] và \[EF//AB;\,\;PQ//AD\].
Biết rằng khi xét trong một hệ tọa độ \[Oxy,\] đường cong trong hình là một phần của đồ thị hàm số bậc ba. Phần chính giữa công viên người ta muốn mắc dây đèn trang trí dọc đoạn thẳng \[MN\] như hình. Biết giá tiền mỗi mét dây trang trí của phần dành cho trẻ em là 140 nghìn đồng và phần dành cho người lớn là 180 nghìn đồng. Tổng số tiền mắc dây đèn trang trí trên đoạn \[MN\] là bao nhiêu triệu đồng.
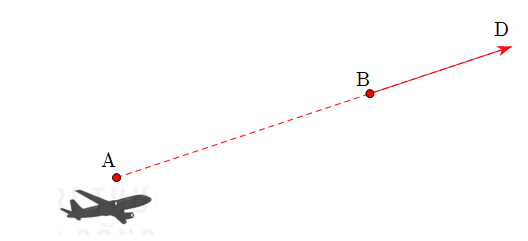
Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm \(A\left( {800;500;7} \right)\) đến điểm \(B\left( {940;550;8} \right)\) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo \(D\left( {x;y;z} \right)\). Khi đó \(x + y + z = ?\)
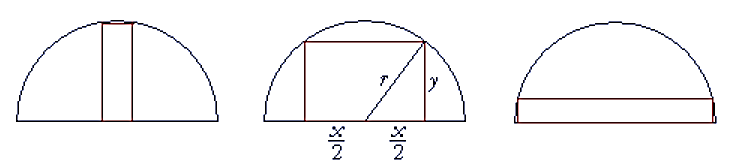
Ông An có một tấm tôn có dạng nửa đường tròn bán kính \(r = 3\) m. Ông muốn cắt ra một hình chữ nhật nội tiếp nửa đường tròn đó để làm biển quảng cáo. Khi biển quảng cáo đó có diện tích lớn nhất thì chiều dài của tấm biển bằng bao nhiêu mét?.
Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật lạ càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc \(v\) của luồng khí liên hệ với bán kính \(x\) của khí quản theo công thức: \(v(x) = k\left( {{x_0} - x} \right) \cdot {x^2}{\rm{ voi }}\frac{1}{2}{x_0} \le x \le {x_0}\) trong đó \(k\) là hằng số \((k > 0)\) và \({x_0}\) là bán kính khí quản ở trạng thái bình thường (Theo James Stewart, J. (2015). Calculus. Cengage Learning). Khi đó \(x = \) \(............\) \({x_0}\) thì vận tốc luồng khí của một cơn ho trong trường hợp này là lớn nhất (làm tròn kết quả đến hàng phần trăm).








