Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 5
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Hàm số \(y = f\left( x \right)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;3} \right]\) cho trong hình bên. Gọi \(M\) là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\). Tìm mệnh đề đúng?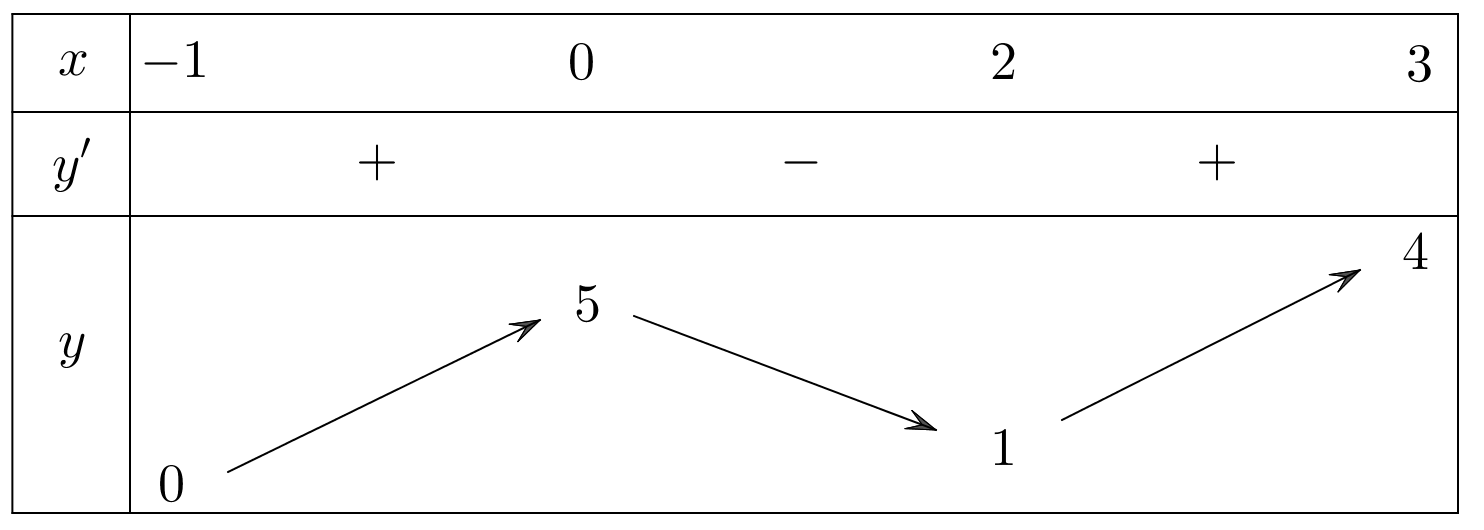
\(M = f\left( 2 \right)\).
\(M = f\left( { - 1} \right)\).
\(M = f\left( 3 \right)\).
\(M = f\left( 0 \right)\).
Trong không gian Oxyz. cho biết \(A\left( { - 2;3;1} \right)\); \(B\left( {2;1;3} \right)\). Điểm nào dưới đây là trung điểm của đoạn \(AB\)?
\[P\left( {0;2;0} \right)\].
\[N\left( {2;2;2} \right)\].
\[M\left( {0;2;2} \right)\].
\[Q\left( {2;2;0} \right)\].
Trong không gian với hệ trục tọa độ Oxyz, cho \(\overrightarrow u = \left( { - 1;\,1;\,0} \right)\), \(\overrightarrow v = \left( {0;\, - 1;\,0} \right)\). Góc giữa hai véc-tơ \(\overrightarrow u \) và \(\overrightarrow v \) là
\({60^o}\).
\({135^o}\).
\({45^o}\).
\({120^o}\).
Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}\)?
\(y = {x^2} + 1\).
\(y = \frac{{x + 1}}{{x + 3}}\).
\(y = {x^4} + {x^2} - 1\).
\(y = {x^3} + x\).
Trong không gian Oxyz, toa độ một vectơ n vuông góc với cả hai vectơ a =(1;1;-2),b = (1:0;3) là
(2;-3;-1).
(3;5; -2)
(2;3; -1).
(3; -5; -1)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau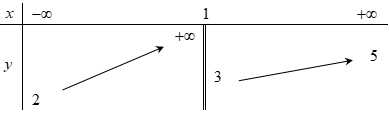
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
\(4\).
\(3\).
\(2\).
\(1\).
Cho hàm số \(y = {x^2} - 6x + m\) (\(m\) là tham số thực) thỏa mãn \(\mathop {\min }\limits_{\left[ {0;4} \right]} y = - 1\). Mệnh đề nào sau đây đúng?
\(m < - 10\).
\( - 10 < m \le - 7\).
\(0 < m < 10\).
\( - 7 < m < 0\).
Trong không gian tọa độ Oxyz, góc giữa hai vectơ \(\overrightarrow i \) và \(\overrightarrow u = \left( { - \sqrt 3 \,;\,0\,;\,1} \right)\) là
\({30^0}\).
\({150^0}\).
\({60^0}\).
\({120^0}\).
Đồ thị hàm số \(y = {x^3} - 3{x^2} + 5x - 4\)có tâm đối xứng là
\(I( - 1; - 1)\).
\(I( - 1;1)\).
\(I(1; - 1)\).
\(I(1;1)\).
Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = \left( {{{\rm{e}}^x} + 1} \right)\left( {{{\rm{e}}^x} - 12} \right)\left( {x + 1} \right){\left( {x - 1} \right)^2}\) trên \(\mathbb{R}\). Hỏi hàm số \(y = f(x)\) có bao nhiêu điểm cực trị?
\(1\).
\(2\).
\(3\).
\(4\).
Bảng biến thiên sau đây là của hàm số nào?
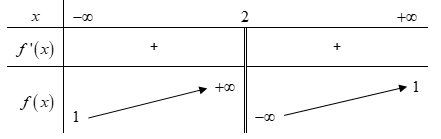
\(f\left( x \right) = \frac{{x + 3}}{{x - 2}}\).
\(f\left( x \right) = \frac{{2x - 3}}{{x - 2}}\).
\[f\left( x \right) = \frac{{x + 3}}{{2 - x}}\].
\[f\left( x \right) = \frac{{x - 3}}{{x - 2}}\].
Trong không gian cho 3 vectơ \[\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \] không đồng phẳng. Xét các vectơ \[\overrightarrow x = 2\overrightarrow a - \overrightarrow b ,\,\,y = - 4\overrightarrow a + 2\overrightarrow b ,\,\,\overrightarrow z = - 3\overrightarrow a - 2\overrightarrow b \]. Khẳng định nào đúng?
Hai vectơ \[\overrightarrow y ,\,\,\overrightarrow z \] cùng phương
Hai vectơ \[\overrightarrow x ,\,\,\overrightarrow z \] cùng phương.
3 vectơ \[\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \] đồng phẳng.
Hai vectơ \[\overrightarrow x ,\,\,\overrightarrow y \] cùng phương
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - m{x^2} + \left( {4\;m - 2} \right)x + 1 - 4\;m}}{{x - 1}}\) có đồ thị là \(\left( C \right)\) với \(m\) là tham số
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\).
c) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\).
d) Có 2 phương trình tiếp tuyến của \(\left( C \right)\) song song với đường thẳng \(x - y = 0\).
Các mệnh đề sau đúng hay sai?
a) không nghịch biến trên R.
b) \(y = - 5x + \sin x\)không nghịch biến trên R.
c) không nghịch biến trên R.
d) \(y = {\left( {\frac{\pi }{{\sqrt 3 + \sqrt 5 }}} \right)^x}\)không nghịch biến trên R.
Dân số của một quốc gia sau \[t\] (năm) bắt đầu từ năm \[2023\] được tính theo công thức \[N\left( t \right) = 100{e^{0,012t}}\] (trong đó \[N\left( t \right)\] được tính bằng triệu người, \[0 \le t \le 50\])
a) Dân số của quốc gia này ở năm \[2030\] vượt mức \[110\] triệu người.
b) Dân số của quốc gia này ở năm \[2035\] vượt mức \[115\] triệu người.
c) Vào năm \[2030\] thì tốc độ tăng dân số là \[1,6\] triệu người/năm.
d) Vào năm \[2026\] thì tốc độ tăng dân số là \[1,6\] triệu người/năm.
Trong không gian Oxyz, cho hình hộp OABC.O'A'B'C' có \(A\left( {1;1; - 1} \right),B\left( {0;3;0} \right),\overrightarrow {BC'} = \left( {2; - 6;6} \right)\)Gọi \(H,K\) lần lượt là trọng tâm của tam giác \(OA'O'\) và \(CB'C'\).
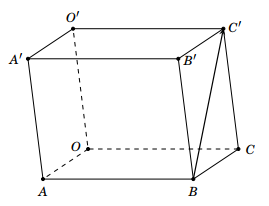
a) Tọa độ véc tơ \(\overrightarrow {HK} = \left( { - 1;2; - 1} \right)\).
b) Tọa độ véc to \(\overrightarrow {AB'} = \left( { - 2;3; - 6} \right)\).
c) Tọa độ điểm \(O'\) là \(\left( {3; - 5;5} \right)\).
d) Tọa độ điểm \(C'\) là \(\left( {2; - 3;6} \right)\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Sự ảnh hưởng khi sử dụng một loại độc tố đối với vi khuẩn \[HP\] được một bác sĩ mô tả với hàm số \[P\left( t \right) = \frac{{2t + 1}}{{4{t^2} + 2t + 4}}\], trong đó \[P\left( t \right)\] là số lượng vi khuẩn \[HP\] sau thời gian \[t\] sử dụng độc tố. Sau khi sử dụng độc tố bao lâu thì số lượng vị khuẩn HP bắt đầu giảm (kết quả được làm tròn đến hàng phần mười)
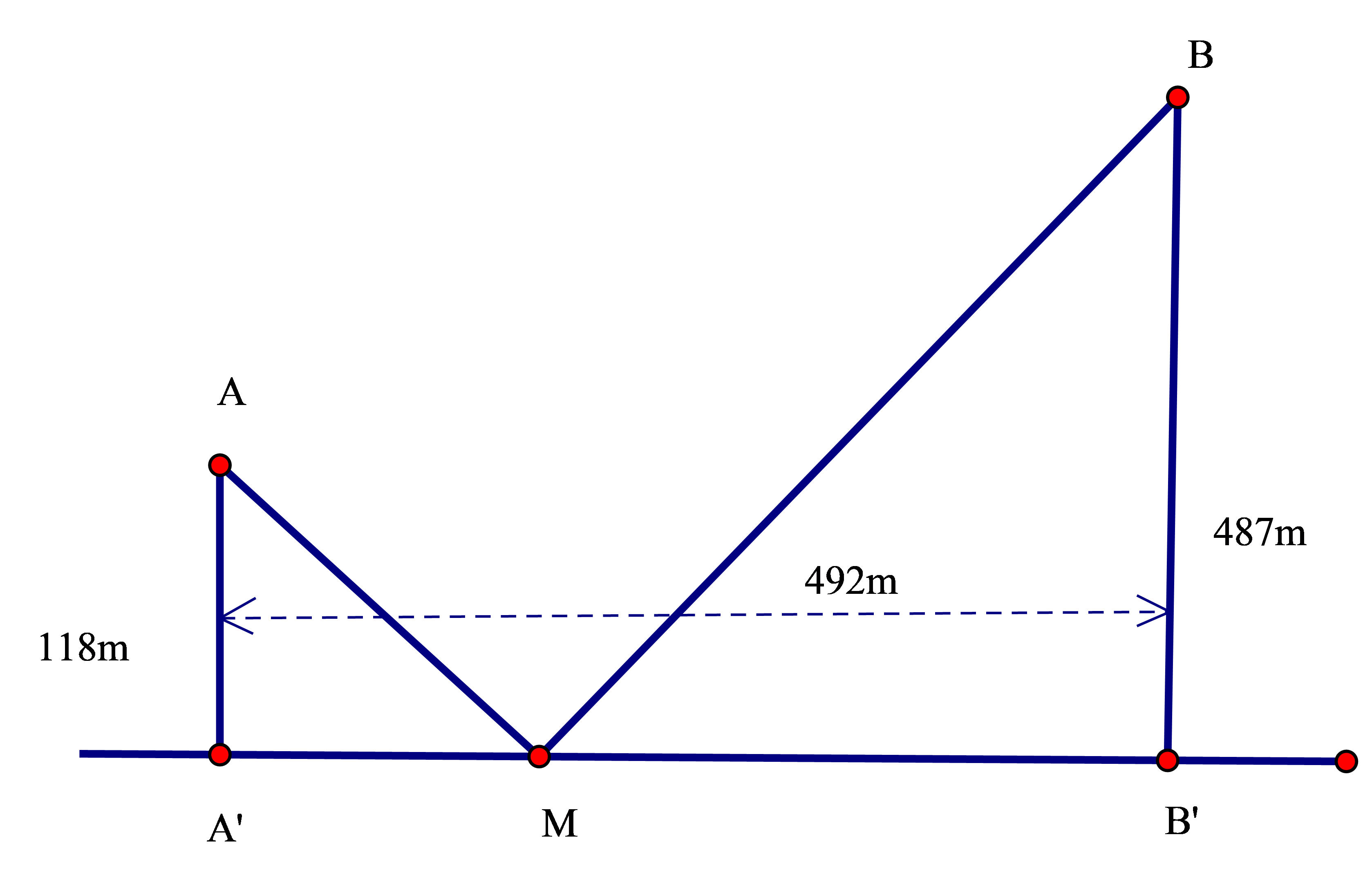
Có hai xã cùng ở một bên bờ sông. Người ta đo được khoảng cách từ trung tâm \[A,B\] của hai xã đó đến bờ sông lần lượt là \[AA' = 118m\], \[BB' = 487m\] và \[A'B' = 492\,m\] (Hình vẽ). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí \[M\] của trạm cung cấp nước sạch đó trên đoạn \[A'B'\] sao cho tổng khoảngcách từ hai vị trí \[A,B\] đến vị trí \[M\] là nhỏ nhất. Tính tổng khoảng cách nhỏ nhất đó (kết quả làm tròn đến hàng đơn vị).
Cho hàm số \[y = \frac{{mx + 2}}{{2x + m}}\], \[m\] là tham số thực. Gọi \[S\] là tập hợp tất cả các giá trị nguyên của tham số \[m\] để hàm số nghịch biến trên khoảng \[\left( {0;1} \right)\]. Tìm số phần tử của \[S\].
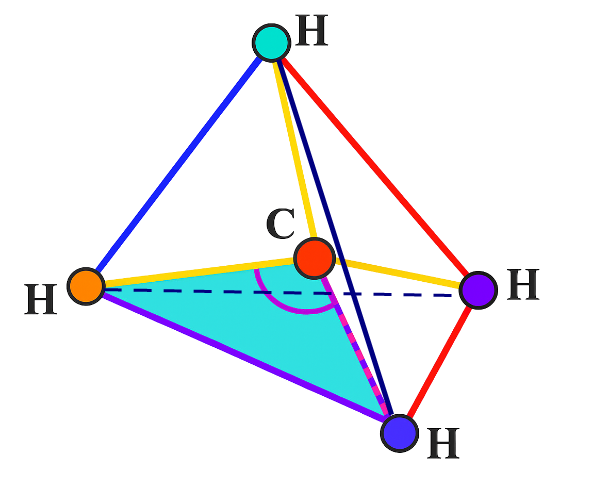
Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó. Một phân tử metan \(C{H_4}\) được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện. Góc liên kết là góc tạo bởi liên kết \(H - C - H\) là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen. Tính số đo góc liên kết này (làm tròn kết quả đến hàng đơn vị của độ).
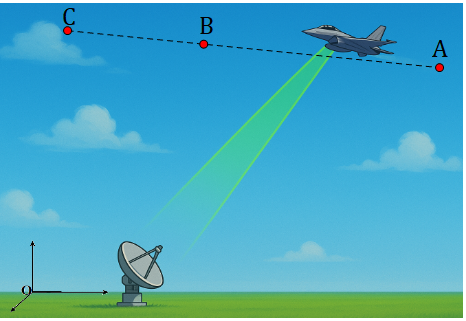
Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilomet), ra đa phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm \[A\left( {800\,;\,500\,;7} \right)\] đến điểm \[B\left( {940\,;\,550\,;\,9} \right)\] trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là điểm \[C\left( {x\,;\,y\,;z} \right)\]. Tính \[x\, + \,y\, + z\]
Một tay lái mô tô nặng 180 (lb), di chuyển với vận tốc không đổi 30 dặm/giờ, thực hiện một khúc cua trên đường cho bởi đồ thị \(y = 100{e^{0,01x}},\quad - 200 \le x \le 50\)
Có thể chứng minh rằng độ lớn của lực pháp tuyến tác dụng lên tay lái mô tô xấp xỉ
\[F(x) = \frac{{10890{e^{0,1x}}}}{{{{\left( {1 + 100{e^{0,2x}}} \right)}^{3/2}}}}\](đơn vị lb)
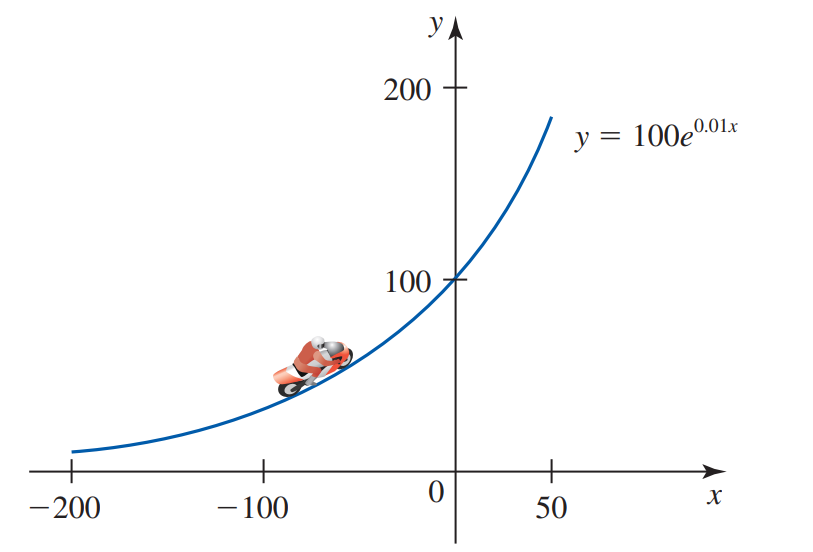
Hãy tìm lực pháp tuyến lớn nhất tác dụng lên tay lái trong suốt khúc cua (làm tròn kết quả đến hàng đơn vị)
