Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 4
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;2} \right]\)và có bảng biến thiên như sau.
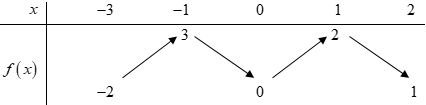
Gọi \[M,{\kern 1pt} \,m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;2} \right]\). Tính \[M + {\kern 1pt} \,m\].
\[1\].
\[3\].
\[4\].
\[2\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau: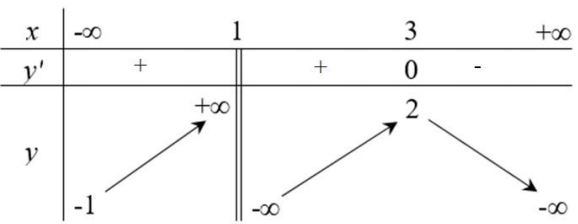
Đồ thị hàm số \[y = f\left( x \right)\] có tổng số bao nhiêu tiệm cận ?
\[3\].
\[2\].
\[1\].
\[0\].
Trong không gian tọa độ Oxyz, cho tam giác ABC có ba đỉnh \[A\left( {a;0;0} \right)\],\[B\left( {0;b;0} \right)\],\[C\left( {0;0;c} \right)\]. Tọa độ trọng tâm của tam giác \[ABC\]là
\(\left( {\frac{a}{3};\frac{b}{3};\frac{c}{3}} \right)\).
\(\left( {a;b;c} \right)\).
\(\left( {\frac{{ - a}}{3};\frac{{ - b}}{3};\frac{{ - c}}{3}} \right)\).
\(\left( { - a; - b; - c} \right)\).
Trong không gian với hệ trục tọa độ Oxyz, cho ba véctơ \(\overrightarrow a = \left( {1;2; - 1} \right),\overrightarrow b = \left( {3; - 1;0} \right),\overrightarrow c = \left( {1; - 5;2} \right)\). Câu nào sau đây đúng?
\(\overrightarrow a \) vuông góc với \(\overrightarrow b \).
\(\overrightarrow a \) cùng phương với \(\overrightarrow b \).
\(\overrightarrow a \),\(\overrightarrow b \),\(\overrightarrow c \) không đồng phẳng.
\(\overrightarrow a \),\(\overrightarrow b \),\(\overrightarrow c \) đồng phẳng.
Trong không gian với hệ tọa độ Oxyz, cho hai véc tơ \(\overrightarrow a = \left( {2;m + 1; - 1} \right)\)và \(\overrightarrow b = \left( {1; - 3;2} \right)\). Với giá trị nào của \(m\) sau đây thì \(\left| {\overrightarrow a .\overrightarrow b } \right| = 3\) ?
\(2\).
\( - 3\).
\(0\).
\(4\).
Hàm số \[y = {x^3} - 2{x^2} + x + 1\] đồng biến trên khoảng nào?
\[\mathbb{R}\backslash \left( { - 1;\,1} \right)\].
\[\left( {0;\,2} \right)\].
\[\left( { - 3;\, - 2} \right)\].
\[\left( { - 1;\,1} \right)\].
Cho hàm số \[f\left( x \right)\] có \[f'\left( x \right) = {x^2}{\left( {x - 2} \right)^3}{\left( {x - 3} \right)^4},\forall x \in \mathbb{R}\]. Số điểm cực đại của hàm số đã cho là
\[0\].
\[3\].
\[1\].
\[2\].
Cho hàm số \(y = \frac{{2x - m}}{{x + 2}}\)với \(m\)là tham số, \(m \ne - 4\). Biết \(\mathop {\min }\limits_{x \in \left[ {0;2} \right]} f\left( x \right) + \mathop {{\rm{max}}}\limits_{x \in \left[ {0;2} \right]} f\left( x \right) = - 8\). Giá trị của tham số \(m\)bằng
\(8\).
\(9\).
\(12\).
\(10\).
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a \ne 0\) có đồ thị như hình vẽ: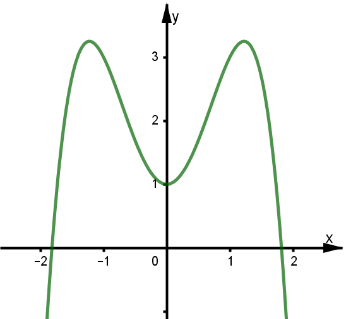
Tìm mệnh đề đúng trong các mệnh đề sau?
\(a < 0\); \(b < 0\); \(c > 0\).
\(a > 0\); \(b < 0\); \(c > 0\).
\(a < 0\); \(b > 0\); \(c > 0\).
\(a < 0\); \(b > 0\); \(c < 0\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ bên. Tìm số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 1\).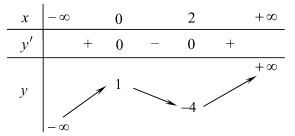
\(4\).
\(6\).
\(5\).
\(0\).
Trong không gian Oxyz, cho tam giác \(MNP\) có \(M\left( {2; - 3;4} \right),N\left( {1;2;3} \right)\) và \(P\left( {3; - 2;2} \right)\). Trọng tâm của tam giác \(MNP\) có tọa độ là:
\(\left( { - 2;1; - 3} \right)\).
\(\left( {6; - 3;9} \right)\).
\(\left( {2; - 1;3} \right)\).
\(\left( { - 6;3; - 9} \right).\)
Hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Tính độ dài vectơ \[\overrightarrow x = \overrightarrow {AA'} + \overrightarrow {AC'} \] theo \(a\).
\(\frac{{a\sqrt 6 }}{2}\).
\(a\sqrt 2 \).
\(\left( {1 + \sqrt 3 } \right)a\).
\(a\sqrt 6 \).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
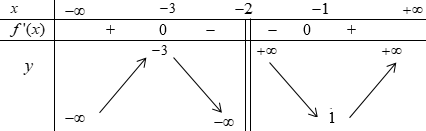
Các mệnh đề sau đúng hay sai?
a) Hàm số nghịch biến trên khoảng \(\left( { - 3; - 1} \right)\).
b) Hàm số đạt cực đại tại điểm \(x = - 3\)và đạt cực tiểu tại \(x = - 1\).
c) Đồ thị hàm số không có điểm chung với trục hoành.
d) Đồ thị hàm số nhận đường thẳng \(x = - 2\)làm tiệm cận đứng.
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen trong một hồ nước sau \(t\) giờ \((t \ge 0)\) khi một lượng rác thải hữu cơ bị xả vào hồ được tính xấp xỉ bởi hàm số
\(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}.\)
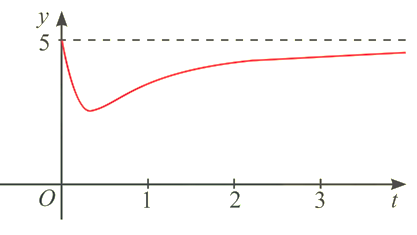
a) Vào thời điểm \(t = 1\) thì nồng độ oxygen trong nước là \(3,5\).
b) Nồng độ oxygen trong một hồ nước không vượt quá \(5\).
c) Vào thời điểm \(t = 0\) thì nồng độ oxygen trong nước cao nhất.
d) Nồng độ oxygen trong một hồ nước thấp nhất là \(3,5\).
Cho hàm số \(y = x - \frac{1}{{x + 1}}\)
a) Đồ thị của hàm số có tiệm cận đứng là \(x = 1\).
b) Đồ thị hàm số cắt trục \(Oy\) tại \(M\). Phương trình tiếp tuyến của tại \(M\) là \(y = 2x - 1\).
c) Tồn tại hai tiếp tuyến của đồ thị vuông góc với nhau.
d) Để đường thẳng \(y = k\) cắt \((C)\) tại hai điểm phân biệt \(A\) và \(B\) sao cho \(OA \bot OB\) khi đó \(k\) là nghiệm của phương trình \({k^2} - k - 1 = 0\).
Trong không gian Oxyz, cho ba điểm \(A\left( {3{\mkern 1mu} ;{\mkern 1mu} 5{\mkern 1mu} ;{\mkern 1mu} - 1} \right)\), \(B\left( {7{\mkern 1mu} ;{\mkern 1mu} x;{\mkern 1mu} 1} \right)\), \(C\left( {9{\mkern 1mu} ;{\mkern 1mu} 2{\mkern 1mu} ;{\mkern 1mu} y} \right)\).
a) Tích vô hướng của \(\overrightarrow {AB} .\overrightarrow {AC} = - 3x + 2y + 41\).
b) Ba điểm \(A,B,C\) thẳng hàng thì \(x + y = 5.\)
c) Tam giác \(ABC\) vuông tại \(A\) thì \(x = 13,y = - 1.\)
d) Điểm \(G\left( {\frac{{19}}{3};\frac{8}{3};3} \right)\) là trọng tâm tam giác \(ABC\) thì \(x = 1;y = 3.\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một vật chuyển động với vận tốc \(\left( {m/s} \right)\) được xác định bởi hàm số \(f(t) = - {t^3} + 3{t^2}\) với \(t \ge 0\). Khi đó \(f\prime (t)\) là gia tốc của vật tại thời điểm \(t\) . Vận tốc của vật đạt được cao nhất trong khoảng thời gian 3 giây đầu là bao nhiêu m/s?
Cho một tấm nhôm có dạng hình vuông cạnh \(6dm\). Bác Ánh cắt ở bốn góc bốn hình vuông cùng có độ dài bằng \(x(dm)\), rồi gập tấm nhôm lại như Hình để được một cái hộp có dạng khối hộp chữ nhật không có nắp. Gọi \(V\) là thể tích của khối hộp đó tính theo \(x\).
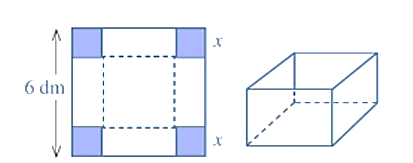
Tìm \(x(dm)\) để khối hộp tạo thành có thể tích lớn nhất.
Một giỏ hoa treo trong nhà làm bằng 3 sợi dây không giãn, mỗi sợi dài \(60\left( {cm} \right)\) miếng kê là một miếng gỗ cân đối hình tròn bán kính \(20\left( {cm} \right)\), ba sợi dây được thắt một đầu bên trên và đỡ giá gỗ tại 3 điểm tạo thành tam giác đều . Biết lực chịu đựng của mỗi sợi dây bằng nhau và mỗi sợi chịu không quá \(15N\) trọng lượng của miếng giá gỗ là \(5N\). Tính trọng lượng tối đa của các chậu hoa để dây treo không bị đứt .
Giả sử chiều cao của một giống cây trồng tuân theo quy luật logistic được mô hình hoá bằng hàm số \(f\left( t \right) = \frac{{200}}{{1 + 4{e^{ - t}}}},\;\;t \ge 0\). Trong đó thời gian \(t\) được tính bằng tháng kể từ khi hạt bắt đầu nảy mầm. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ tăng chiều cao của giống cây đó. Hỏi sau khi hạt giống bắt đầu nảy mầm thì sau bao nhiêu tháng tốc độ tăng chiều cao của cây là lớn nhất?
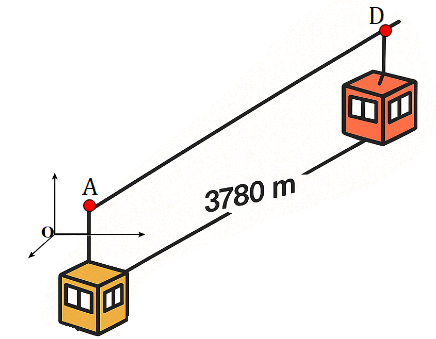
Trong không gian với hệ tọa độ Oxyz , một cabin cáp treo xuất phát từ điểm \(A\left( {10;\,3;\,0} \right)\) và chuyển động đều theo đường cáp thẳng đến vị trí \(D\) cách điểm \(A\) một khoảng \(3780\,{\rm{m}}\). Biết đường đi của cabin cùng phương với vectơ \(\vec u = \left( {2;\, - 2;\,1} \right)\) và sau 3 phút kể từ khi xuất phát thì cabin đi đến vị trí \(B\) có hoành độ \({x_B} = 550\). Hỏi thời gian di chuyển của cabin trên quãng đường \(AD\) là bao nhiêu giây?
Cho một tấm nhôm hình lục giác đều cạnh \[90\] cm. Người ta cắt ở mỗi đỉnh của tấm nhôm hai hình tam giác vuông bằng nhau, biết cạnh góc vuông nhỏ bằng \[x\] rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm \[x\] để thể tích của khối lăng trụ lục giác đều trên là lớn nhất .
![Cho một tấm nhôm hình lục giác đều cạnh \[90\] cm. Người ta cắt ở (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/21-1761612074.png)
