Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 3
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {1;0;1} \right)\)và \(B\left( {4;2; - 2} \right)\). Độ dài đoạn thẳng \(AB\)bằng
\(2\).
\(\sqrt {22} \).
\(4\).
\(22\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như hình vẽ sau: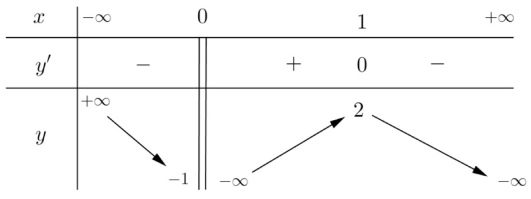 Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số \[y = f\left( x \right)\] là
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số \[y = f\left( x \right)\] là
\(2\).
\(1\).
\(0\).
\(3\).
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 4x - 2y + 6z + 5 = 0.\) Mặt cầu \(\left( S \right)\) có bán kính là ?
\(3.\)
\(2.\)
\(5.\)
\(7.\)
Trong không gian Oxyz, cho hai véctơ \(\overrightarrow a = \left( {1;0; - 3} \right)\) và \(\overrightarrow b = \left( {3;1;2} \right)\). Tính tọa độ véctơ \(\overrightarrow a + \overrightarrow b \).
\(\left( {2;1;5} \right)\).
\(\left( { - 2;1; - 5} \right)\).
\(\left( {4;1;5} \right)\).
\(\left( {4;1; - 1} \right)\).
Trong các hàm số sau, hàm số nào đồng biến trên \[\mathbb{R}\]?
\[y = {x^3} - x\].
\[y = {x^3} + x\].
\[y = {x^2} + 1\].
\[y = {x^4} + 2{x^2}\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ.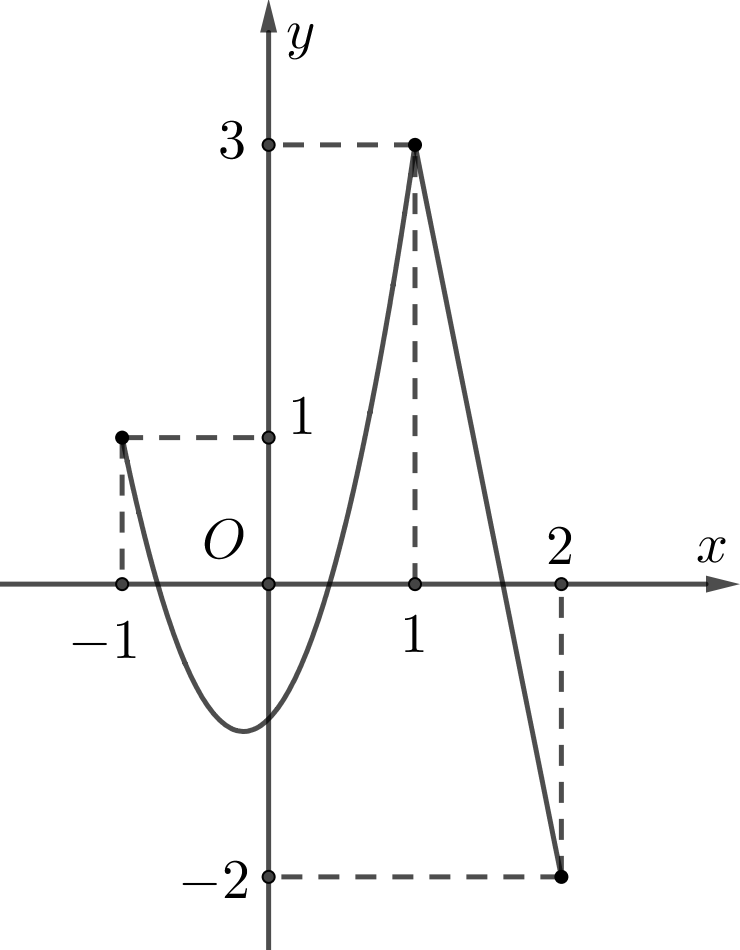 Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1;2} \right].\) Ta có \(M + m\) bằng
Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1;2} \right].\) Ta có \(M + m\) bằng
\(2\).
\(4\).
\(1\).
\(0\).
Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\)(với \(m > 1\)). Tìm giá trị của tham số \(m\) để hàm số có giá trị lớn nhất trên đoạn \(\left[ {1;4} \right]\) bằng \(3\).
\(m = 3\).
\(m = 2\).
\(m = 5\).
\(m = 4\).
Bảng biến thiên sau đây là của hàm số nào? 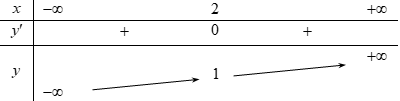
\[y = {x^3} + 3{x^2} - 3x.\]
\[y = - {x^3} - 3{x^2} - 3x.\]
\[y = {x^3} - 3{x^2} + 3x.\]
\[y = - {x^3} + 3{x^2} - 3x.\]
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ sau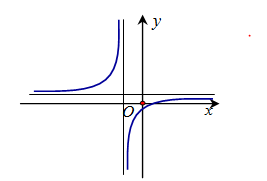 Khẳng định nào sau đây là khẳng định đúng?
Khẳng định nào sau đây là khẳng định đúng?
\(\left\{ {\begin{array}{*{20}{c}}{ad < 0}\\{bc < 0}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{ad < 0}\\{bc > 0}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{ad > 0}\\{bc > 0}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{ad > 0}\\{bc < 0}\end{array}} \right.\).
Cho hình hộp\[ABCD.EFGH\] có\(\overrightarrow {AB} = \overrightarrow a ,\,\overrightarrow {AD} = \overrightarrow b ,\,\overrightarrow {AE} = \overrightarrow c .\) Gọi \(I\) là điểm thuộc đoạn thẳng \(BG\) sao cho \(4BI = BG\). Biểu thị \(\overrightarrow {AI} \) qua \(\overrightarrow a ,\,\;\overrightarrow b ,\,\;\overrightarrow c \) ta được
\(\overrightarrow {AI} = \overrightarrow a + \frac{7}{4}\overrightarrow b + \frac{7}{4}\overrightarrow c \).
\(\overrightarrow {AI} = \overrightarrow a + \frac{1}{2}\overrightarrow b + \frac{1}{2}\overrightarrow c \).
\(\overrightarrow {AI} = \overrightarrow a + \frac{1}{3}\overrightarrow b + \frac{1}{3}\overrightarrow c \).
\(\overrightarrow {AI} = \overrightarrow a + \frac{1}{4}\overrightarrow b + \frac{1}{4}\overrightarrow c \).
Trong không gian với hệ tọa độ Oxyz, cho \(M\left( {1;\;2;\;3} \right)\), \(N\left( {2;\; - 3;\;1} \right)\), \(P\left( {3;\;1;\;2} \right)\). Tìm tọa độ điểm \(Q\) sao cho \(MNPQ\) là hình bình hành.
\[Q\left( {4;\; - 4;\;0} \right)\].
\[Q\left( {2;\;6;\;4} \right)\].
\[Q\left( { - 4;\; - 4;\;0} \right)\].
\[Q\left( {2;\; - 6;\;4} \right)\].
Cho hàm số \[y = f(x)\] liên tục trên đoạn \[{\rm{[}}a,b{\rm{]}}\]và có đồ thị \[y = f'(x)\]trên đoạn \[y = f'(x)\] hình vẽ bên .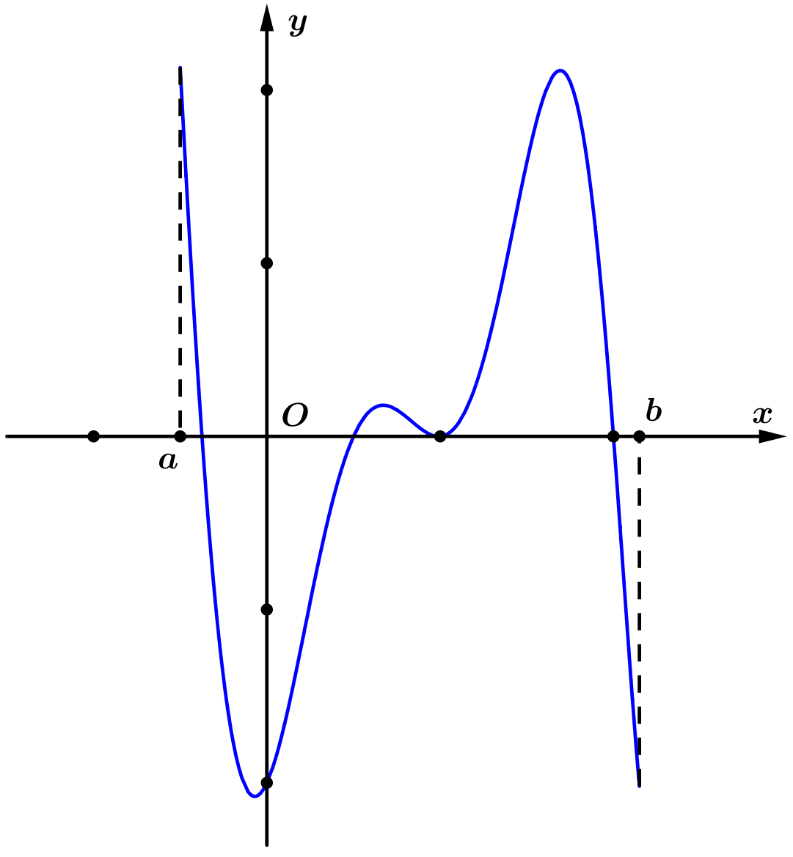 Trên đoạn \[{\rm{[}}a,b{\rm{]}}\] hàm số \[y = f(x)\] có bao nhiêu điểm cực trị\[?\]
Trên đoạn \[{\rm{[}}a,b{\rm{]}}\] hàm số \[y = f(x)\] có bao nhiêu điểm cực trị\[?\]
5.
3.
2.
4.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - {x^2} + 2(m + 1)x - 5}}{{x - 1}}\).
a) Để hàm số có cực đại, cực tiểu thì \(m > 4\).
b) Khi \(m = 0\) thì đồ thị hàm số không cắt \(Ox\).
c) Khi \(m = 0\) thì đồ thị hàm số có tiệm cận xiên là \(y = - x + 1\).
d) Tồn tại 1 điểm \(M\) thuộc đồ thị \((C)\) sao cho \({x_M} > 1\) và độ dài \(IM\) ngắn nhất (\[I\] là tâm đối xứng của \((C)\)) khi đó tung độ \({y_M} < - 4\).
Cho 3 điểm \(A\left( { - 1\,;\,2;\,1} \right);B\left( {2; - 2;4} \right);C\left( {0; - 4;1} \right)\).
a) Điểm \(D\left( {5; - 6;7} \right)\). Khi đó 3 điểm \(A,B,D\) thẳng hàng.
b) Ba điểm \(A,\,B,C\) không thẳng hàng.
c) Cho \(\overrightarrow u \left( {x - 1;2y + 1;3z - 5} \right)\) thoả mãn \(\overrightarrow u \bot \overrightarrow {AB} ;\overrightarrow u \bot \overrightarrow {AC} \). Khi đó \({x^2} + {y^2} + {z^2} = 2024\)
d) \[cos\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \frac{{37}}{{\sqrt {1258} }}\].
Nhà máy \[A\] chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy \[B\]. Hai nhà máy thoả thuận rằng, hằng tháng \[A\] cung cấp cho \[B\] số lượng sản phẩm theo đơn đặt hàng của \[B\] (tối đa \[100\] tấn sản phẩm). Nếu số lượng đặt hàng là \[x\] tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P\left( x \right) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để \[A\] sản xuất \[x\]tấn sản phẩm trong một tháng là \(C\left( x \right) = 100 + 30x\) (triệu đồng) (gồm \[100\] triệu đồng chi phí cố định và \[30\] triệu đồng cho mỗi tấn sản phẩm).
a) Chi phí để \[A\] sản xuất \[10\] tấn sảm phẩm trong một tháng là \[400\] triệu đồng.
b) Số tiền \[A\] thu được khi bán \[10\] tấn sản phẩm cho \[B\] là \[600\] triệu đồng.
c) Lợi nhuận mà \[A\] thu được khi bán \[x\] tấn sản phẩm \(\left( {0 \le x \le 100} \right)\) cho \[B\] được biểu diễn bằng công thức \( - 0,01{x^3} + 15x - 100\).
d) \[A\]bán cho \[B\] khoảng \[70,7\] tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất.
Cho hàm số \(y = {x^3} - 3m{x^2} - 9{m^2}x\) (tham số \[m\]). Khi đó:
a) Biết hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\) khi \(m \le a\) hoặc \(m \ge b\), khi đó \(a + b = \frac{2}{3}\)
b) Khi \(m = 1\) thì hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\)
c) Nếu \(m > 0\) thì hàm số nghịch biến trên khoảng \(\left( { - m;3m} \right)\).
d) Nếu \(m < 0\) thì hàm số nghịch biến trên khoảng \(\left( {3m;\; - m} \right)\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Ngày khai giảng năm học \(2024 - 2025\). Học sinh khối \(12\) trường THPT Nguyễn Hiền thả chùm bóng bay gắn thông điệp “Học Sinh khối \(12\) chiến thắng CT\(2018\)”. Ước tính độ cao \(h\)(tính bằng\(km\)) của chùm bóng bay so với mặt đất vào thời điểm\(t\) (đơn vị giờ) được cho bởi công thức \(h\left( t \right) = - {t^3} + 3{t^2},\left( {0 \le t \le 3} \right)\). Chùm bóng bay đạt độ cao lớn nhất so với mặt đất là: \(a\left( {km} \right)\). Tìm \(a?\)
Trên mảnh đất hình chữ nhật \(ABCD\) có diện tích \(25{{\rm{m}}^2}\), người chủ lấy một phần đất để trồng cỏ. Biết phần đất trồng cỏ này có dạng hình chữ nhật với hai đỉnh đối diện là \(A\) và \(H\), với \(H\) thuộc cạnh \(BD\). Biết chi phí trồng cỏ là \(80\) (nghìn đồng)\(/{{\rm{m}}^2}\). Hỏi số tiền lớn nhất người chủ cần chuẩn bị để trồng cỏ (miền tô đậm) là bao nhiêu (nghìn đồng)?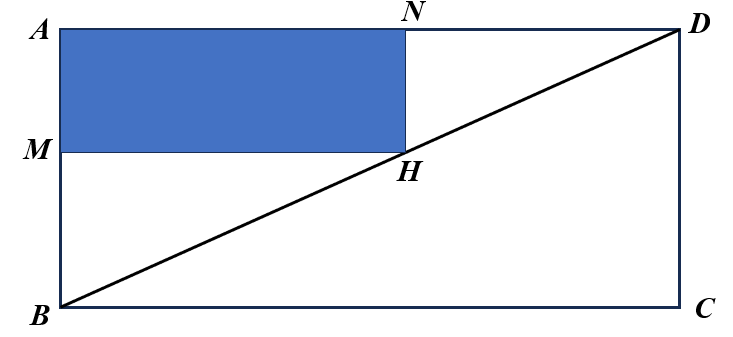
Một con thuyền rời bến \(O(0,0)\) trên một bờ sông, luôn đi với vận tốc không đổi 20 dặm/giờ hướng về bến \(A(1000,0)\) (phía đông của \(O\)); đồng thời nước sông chảy ngược lên phía bắc với tốc độ 5 dặm/giờ. Người ta cho rằng đường đi của thuyền là \(y = 500\left[ {{{\left( {\frac{{1000 - x}}{{1000}}} \right)}^{3/4}} - {{\left( {\frac{{1000 - x}}{{1000}}} \right)}^{5/4}}} \right],\quad 0 \le x \le 1000\)Tìm độ lệch bắc lớn nhất mà thuyền đạt được trong suốt hành trình.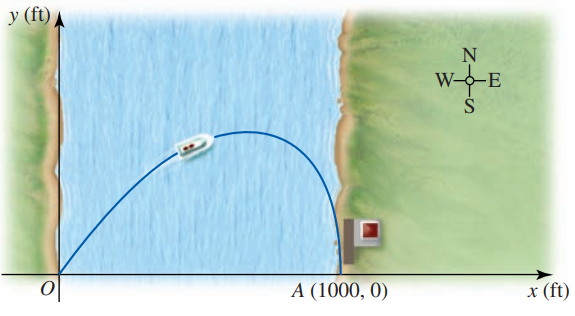
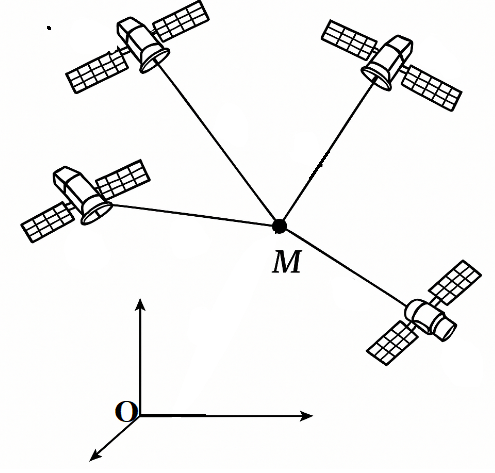
Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác định vị trí của một vật thể trong không gian. Trong cùng một thời điểm, vị trí của một điểm M trong không gian sẽ được xác định bởi bốn vệ tinh cho trước nhờ các bộ thu phát tín hiệu đặt trên các vệ tinh. Giả sử trong không gian với hệ tọa độ \(Oxyz\), có bốn vệ tinh lần lượt đặt tại các điểm \(A(3;1;0)\), \(B(3;6;6)\), \(C(4;6;2)\), \(D(6;2;14)\); vị trí \(M(a;b;c)\) thỏa mãn \(MA = 3\), \(MB = 6\), \(MC = 5\), \(MD = 13\). Khoảng cách từ điểm \(M\) đến điểm \(O\) bằng bao nhiêu?
Giả sử chi phí để xuất bản \(x\) cuốn tạp chí được cho bởi công thức: \(C(x) = 0,0001{x^2} - 0,1x + 10000\), trong đó \(C(x)\) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn tạp chí là 3 nghìn đồng. Ta gọi \(T(x)\) là tổng chi phí bao gồm chi phí xuất bản và chi phí phát hành cho \(x\) cuốn tạp chí. Tỉ số \(M(x) = \frac{{T(x)}}{x}\) được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản \(x\) cuốn. Tìm chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá 30000 cuốn?
Một chiếc ô tô được đặt trên mặt đáy dưới cùa một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA,EB,EC,ED\) có độ dài bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \(60^\circ \) (hình vẽ).
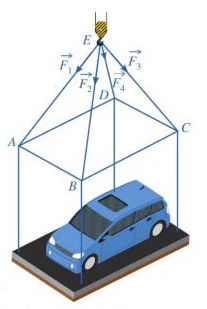
Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Trọng lượng của chiếc xe ô tô bằng bao nhiêu Niutơn? (làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} ,\,\overrightarrow {{F_4}} \) đều có cường độ là \(3500N\) và trọng lượng của khung sắt là \(2500N\).








