Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 2
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho \(\overrightarrow a = \left( { - 2;\,1;\,3} \right)\), \(\overrightarrow b = \left( {1;\,2;\,m} \right)\). Vectơ \(\overrightarrow a \) vuông góc với \(\overrightarrow b \) khi
\(m = 2\).
\(m = - 1\).
\(m = 0\).
\(m = 1\).
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
\(y = \frac{{x - 2}}{{ - x + 2}}\).
\(y = \frac{{ - x + 2}}{{x + 2}}\).
\(y = \frac{{x - 2}}{{x + 2}}\).
\(y = \frac{{x + 2}}{{ - x + 2}}\).
Trong không gian Oxyz, cho hai điểm \(A\left( {1\,;\,0\,;\,1} \right)\) và \(B\left( { - 1\,;\,2\,;\,5} \right)\). Tọa độ trung điểm của đoạn thẳng \(AB\) là
\(\left( {0\,;\,2\,;\,6} \right)\).
\(\left( { - 2\,;\,2\,;\,4} \right)\).
\(\left( {0\,;\,1\,;\,3} \right)\).
\(\left( { - 1\,;\,1\,;\,2} \right)\).
Giá trị nhỏ nhất của hàm số có bảng biến thiên sau trên đoạn \[\left[ { - 2\,;\,3} \right]\] là
\[\mathop {\min }\limits_{\left[ { - 2\,;3} \right]} y = 0\].
\[\mathop {\min }\limits_{\left[ { - 2\,;3} \right]} y = 7\].
\[\mathop {\min }\limits_{\left[ { - 2\,;3} \right]} y = 1\].
\[\mathop {\min }\limits_{\left[ { - 2\,;3} \right]} y = - 3\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là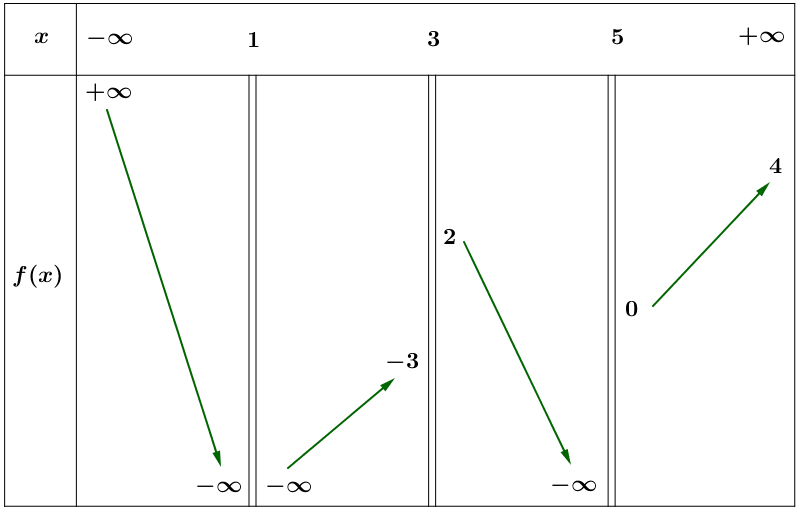
\(3.\)
\(2.\)
\(5.\)
\(4.\)
Trong hệ trục Oxyz cho mặt cầu có phương trình \({x^2} + {y^2} + {z^2} - 2x + 4y + 6z - 1 = 0.\,\)Xác định tâm và bán kính của mặt cầu.
\(I\left( {1; - 2; - 3\,} \right),R = 4\).
\(I\left( {\, - 1;2;3\,} \right),R = \sqrt {15} \).
\(I\left( {\,1; - 2; - 3\,} \right),\,\,R = \sqrt {15} \).
\(I\left( {\,1;2;3\,} \right),\,R = \sqrt {15} \).
Trong không gian Oxyz cho \(A\left( { - 1\,;\,4\,;\,2} \right),\)\(B\left( {3\,;\,2\,;\,1} \right),\)\(C\left( { - 2\,;\,0\,;\,2} \right).\) Tìm tất cả các điểm \(D\) sao cho \(ABCD\) là hình thang có đáy \(AD\) và diện tích hình thang \(ABCD\) gấp ba lần diện tích tam giác \(ABC.\)
\(D\left( {9\,;\, - 6\,;\,2} \right).\)
\(D\left( { - 11\,;\,0\,;\,4} \right).\)
\(D\left( {11\,;\,0\,;\, - 4} \right)\) và \(D\left( { - 9\,;\,6\,;\, - 2} \right).\)
\(D\left( { - 11\,;\,0\,;\,4} \right)\) và \(D\left( {9\,;\, - 6\,;\,2} \right).\)
Tâm đối xứng của đồ thị \(y = {x^3} - x + 2\).
\(\left( {1;2} \right)\).
\(\left( { - 1;2} \right)\).
\(\left( {0;2} \right)\).
\(\left( {0; - 2} \right)\).
Cho hàm số \[y = \frac{{x + m}}{{x + 1}}\] thỏa mãn: \(\mathop {\min }\limits_{\left[ {1;2} \right]} y + \mathop {\max }\limits_{\left[ {1;2} \right]} y = \frac{{16}}{3}\). Mệnh đề nào sau đây đúng?
\[2 < m \le 4\].
\[m \le 0\].
\[m > 4\].
\[0 < m \le 2\].
Cho tứ diện \[ABCD\]. Gọi \[M\] là trung điểm của đoạn thẳng \[BC\]. Đặt \[\overrightarrow {AB} = \overrightarrow a ,\,\,\overrightarrow {AC} = \overrightarrow b ,\,\,\overrightarrow {AD} = \overrightarrow c \]. Đẳng thức nào sau đây là đúng?
\(\overrightarrow {DM} = \frac{1}{2}\left( { - 2\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow a - 2\overrightarrow b + \overrightarrow c } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow a + 2\overrightarrow b - \overrightarrow c } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \right)\).
Cho đồ thị \[\left( C \right)\] của hàm số \[y = f\left( x \right)\] có \[y'{\rm{ = }}\left( {1 + x} \right){\left( {x + 2} \right)^4}{\left( {x - 3} \right)^3}\left( {1 - {x^2}} \right)\]. Trong các mệnh đề sau, tìm mệnh đề đúng:
\[\left( C \right)\]có bốn điểm cực trị .
\[\left( C \right)\]có một điểm cực trị.
\[\left( C \right)\]có ba điểm cực trị.
\[\left( C \right)\]có hai điểm cực trị.
Cho hàm số \(f\left( x \right) = \frac{{ax - 1}}{{bx + c}}\) (\(a\), \(b\), \(c \in \mathbb{R}\)) có bảng biến thiên như sau: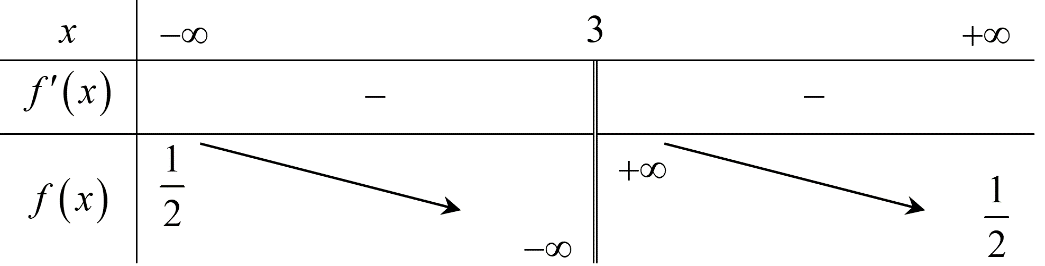
Khẳng định nào dưới đây là đúng?
\(0 < b < \frac{2}{3}\).
\(\left[ \begin{array}{l}b > \frac{1}{6}\\b < 0\end{array} \right.\).
\(0 < b < \frac{1}{6}\).
\(\left[ \begin{array}{l}b > \frac{2}{3}\\b < 0\end{array} \right.\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Quãng đường của một vật chuyển động theo thời gian được cho bởi công thức \[s(t) = - {t^3} + 18{t^2}\], trong đó \[t\](giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \[s\](mét) là quãng đường vật di chuyển được trong thời gian đó.
a) Quãng đường vật di chuyển được sau thời gian 5 giây kể từ lúc chuyển động là \[300m\].
b) Vận tốc của vật tại thời điểm \[t = 5\] (giây) là \[105m/s\].
c) Vận tốc của vật đạt cực đại sau 8 giây kể từ lúc vật bắt đầu chuyển động.
d) Trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là 108 m/s.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
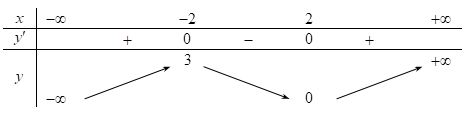
Khi đó:
a) Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
b) Hàm số có và \({y_{CT}} = 0\).
c) Hàm số có ba điểm cực trị
d) Điểm cực tiểu của đồ thị hàm số thuộc đường thẳng \(2x + 2y - 4 = 0\)
Các mệnh đề sau đúng hay sai?
a) Trong không gian với hệ trục toạ độ \(Oxyz\), cho các vectơ \(\vec a = \left( {1;2;1} \right)\), \(\vec b = \left( { - 2;3;4} \right)\), \(\vec c = \left( {0;1;2} \right)\) và \(\vec d = \left( {4;2;0} \right)\). Biết rằng \(\vec d = x.\vec a + y.\vec b + z.\vec c\). Giá trị \(x + y + z\) là 1
b) Trong không gian với hệ tọa độ \[Oxyz\], cho tam giác \(ABC\) có \(\overrightarrow {AB} = \left( { - 3\,;\,0\,;\,4} \right)\), \[\overrightarrow {AC} = \left( {5\,;\, - 2\,;\,4} \right)\]. Độ dài đường trung tuyến \(AM\) là\(3\sqrt 2 \)
c) Trong không gian với hệ tọa độ \[Oxyz\], hình chiếu của điểm \(M\left( {1; - 3; - 5} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là\(\left( {0; - 3;0} \right)\)
d) Trong không gian, cho hai điểm \[A\left( { - 2\,;\,2\,;\, - 1} \right)\], \[B\left( {0\,;\, - 1\,;\, - 2} \right)\]. Tọa độ điểm \[M\]thuộc mặt phẳng \[\left( {Oxy} \right)\]sao cho ba điểm \[A\,,\,B\,,\,M\]thẳng hàng là\[M\left( { - 4\,;\,5\,;\,0} \right)\]
Cho hàm số \(y = x - \frac{1}{{x + 1}}\)
a) Đồ thị của hàm số có tiệm cận đứng là \(x = 1\).
b) Đồ thị hàm số cắt trục \(Oy\) tại \(M\). Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\) là \(y = 2x - 1\).
c) Tồn tại hai tiếp tuyến của đồ thị vuông góc với nhau.
d) Để đường thẳng \(y = k\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(A\) và \(B\) sao cho \(OA \bot OB\) khi đó \(k\) là nghiệm của phương trình \({k^2} - k - 1 = 0\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Sau khi kinh tế suy giảm, giá thuê văn phòng cao ngất ngưởng cuối thập niên 1990 bắt đầu hạ nhiệt. Hàm \(R(t)\) cho giá thuê (USD/ \(f{t^2}\)) của văn phòng hạng A ở khu Back Bay và Financial District (Boston) từ đầu 1997 \((t = 0)\) đến đầu \(2002(t = 5)\) là\[R(t) = - 0,711{t^3} + 3,76{t^2} + 0,2t + 36,5;\quad 0 \le t \le 5.\]Hỏi giá thuê cao nhất trong giai đoạn này là bao nhiêu? (làm tròn kết quả đến hàng phần mười)
Cho 3 lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc với nhau và có độ dài lần lượt là \(2\left( N \right),3\left( N \right),4\left( N \right)\). Biết rằng độ lớn hợp lực của ba lực đã cho bằng \(a\left( N \right)\). Hãy xác định \(a\) (làm tròn đến chữ số hàng phần trăm).
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao \(30{\rm{\;m}}\) và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn. Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ \(Oxyz\) (đơn vị độ dài trên mỗi trục là 1 m), các đỉnh của bốn chiếc cột lần lượt là các điểm \(M\left( {90;0;30} \right),N\left( {90;120;30} \right),P\left( {0;120;30} \right),Q\left( {0;0;30} \right)\) (Hình vẽ). Giả sử \({K_0}\) là vị trí ban đầu của camera có cao độ bằng 25 và \({K_0}M = {K_0}\;N = {K_0}P = {K_0}Q\). Để theo dõi quả bóng đến vị trí \(A\), camera được hạ thấp theo phương thẳng đứng xuống điểm \({K_1}\) có cao độ bằng 19. (Nguồn: https:/mww.abiturloesumg.de; Abitur Bayern 2016 Geometrie V).
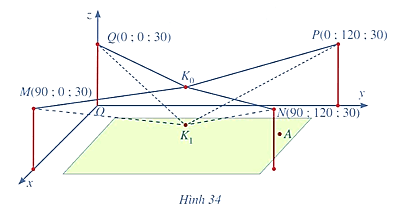
Tọa độ véctơ \(\overrightarrow {{K_0}{K_1}} = \left( {a;b;c} \right)\) với \(a,\,b,\,c\) là các số thực. Tính \(P = a + b + 3c\)?
Cho hàm số \(y = \frac{{\ln x - 6}}{{\ln x - 2m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;e} \right)\). Tìm số phần tử của \(S\).
Một hộ kinh doanh sản xuất mỗi ngày được \(x\) sản phẩm, \(\left( {1 \le x \le 20} \right)\). Chi phí sản xuất \(x\) sản phẩm được cho bởi \(C\left( x \right) = {x^3} - 3{x^2} + 80x + 500\)(nghìn đồng). Giả sử hộ kinh doanh này bán mỗi sản phẩm với giá \(320\) nghìn đồng. Lợi nhuận lớn nhất mà hộ kinh doanh có được là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
Một khách sạn có 30 phòng. Chủ khách sạn nhận thấy nếu cho thuê mỗi phòng với giá 1 000 000 đồng/ngày thì tất cả các phòng đều được thuê hết và cứ tăng giá thêm 50 000 đồng một phòng thì sẽ bị trống thêm 1 phòng. Hỏi chủ khách sạn nên cho thuê mỗi phòng với giá bao nhiêu triệu đồng một ngày để tổng doanh thu một ngày là lớn nhất?








