Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 11
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Hàm số \(y = 2{x^4} - 4{x^2} - 1\) đồng biến trên những khoảng nào?
\(\left( { - \infty ; - 1} \right)\)và\(\left( {0;1} \right)\).
\(\left( { - \infty ; - 1} \right)\) và\(\left( {1; + \infty } \right)\).
\(\left( { - 1;0} \right)\)và\(\left( {1; + \infty } \right)\).
\(\left( { - 1;1} \right)\backslash \left\{ 0 \right\}\).
Cho hàm số \(y = f\left( x \right)\)xác định trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên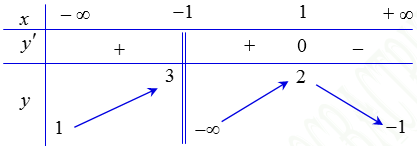
Hỏi khẳng định nào dưới đây là khẳng định sai?
Hàm số đã cho không có đạo hàm tại điểm \(x = - 1\).
Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng \(y = - 1\)và \(y = 1\).
Hàm số đã cho đạt cực đại tại điểm \(x = 1\).
Đồ thị hàm số đã cho không có tiệm cận đứng.
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm \(A\left( { - 1;3;2} \right)\) và \(B\left( {3;1;0} \right).\) Độ dài đoạn thẳng \(AB\) bằng
\(2\sqrt 6 \).
\(3\).
\(4\).
\(2\sqrt 3 \).
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x - 3 = 0\). Bán kính mặt cầu bằng
\(R = 4.\)
\(R = 3.\)
\(R = 5.\)
\(R = 2.\)
Cho hàm số \[f\left( x \right)\] xác định, liên tục trên \[\mathbb{R}\] và có bảng biến thiên sau. Khẳng định nào sau đây đúng?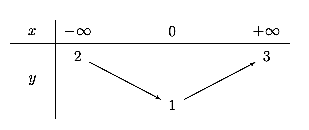 
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = 1\].
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = 2\].
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = 3\].
\[\mathop {{\rm{max}}}\limits_\mathbb{R} f\left( x \right) = 3\].
Trong không gian \[{\rm{Ox}}yz\]cho điểm \[A\]thỏa mãn \[\overrightarrow {OA} = 2\overrightarrow i + \overrightarrow j \]với \[\overrightarrow i ,\,\overrightarrow j \]là hai vectơ đơn vị trên hai trục \[Ox\], \[Oy\]. Tọa độ điểm \[A\]là
\[A\left( {0\,;\,2\,;\,1} \right)\].
\[A\left( {1\,;\,1\,;\,1} \right)\].
\[A\left( {0\,;\,1\,;\,1} \right)\].
\[A\left( {2\,;\,1\,;\,0} \right)\].
Trong không gian tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' với các đỉnh \[A( - 1;1;2)\]\[B( - 3;2;1)\],\[D(0; - 1;2)\]và \[A'(2;1;2)\]. Tìm tọa độ đỉnh \[C'\].
\[C'(1;0;1)\].
\[C'( - 1;3;1)\].
\[C'(0;1;0)\].
\[C'( - 3;0;3)\].
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 3} \right)^3}{\left( {x - 1} \right)^2}\). Số điểm cực trị của hàm số đã cho là
\(3\).
\(2\).
\(1\).
\(0\).
Số điểm có tọa độ là các số nguyên của đồ thị hàm số: \[y = \frac{{2x + 3}}{{x - 1}}\]là
\[4\].
\[3\].
\[1\].
\[2\].
Gọi \(m\) là giá trị để hàm số \(y = \frac{{x - {m^2}}}{{x + 8}}\) có giá trị nhỏ nhất trên \(\left[ {0;\;3} \right]\) bằng \( - 2\). Mệnh đề nào sau đây là đúng?
\(\left| m \right| = 5\).
\(3 < m < 5\).
\(\left| m \right| < 5\).
\({m^2} \ne 16\).
Cho hình lăng trụ \[ABC.A'B'C'\]. \[M\] là trung điểm của \[BB'\]. Đặt \[\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {AA'} = \overrightarrow {c.} \] Khi đó
\[\overrightarrow {AM} = - \frac{{\overrightarrow a }}{2} + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AM} = \overrightarrow a - \frac{{\overrightarrow b }}{2} + \overrightarrow c \].
\[\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{{\overrightarrow b }}{2}\].
\[\overrightarrow {AM} = - \overrightarrow a + \overrightarrow b + \frac{{\overrightarrow c }}{2}\].
Trên đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 4}}\) có bao nhiêu điểm có tọa độ nguyên?
\(4.\)
\(6.\)
\(0.\)
\(2.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f\left( x \right) = \frac{{{x^2} + 4x + 2}}{{x + 2}}\).
a) \(f\left( x \right) = x + 2 - \frac{2}{{x + 2}},\,\forall x \in \left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right)\).
b) Đồ thị hàm số có tiệm cận đứng là đường \(x = 2\).
c) Đồ thị hàm số có đường tiệm cận xiên là \(y = x + 2\).
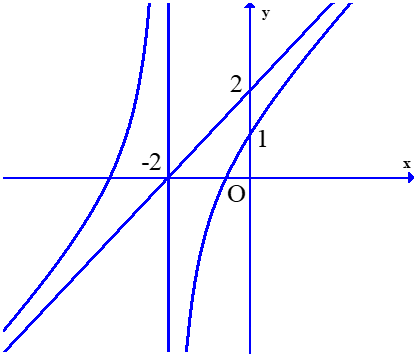
d) Hàm số đã cho có đồ thị hàm số như hình vẽ.
Cho hàm số \(y = f(x)\) có bảng biến thiên dưới đây:
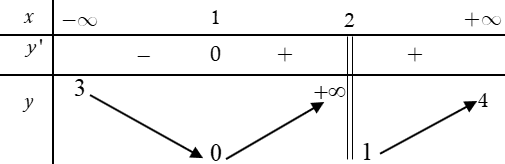
Xét tính đúng sai của các khẳng định sau:
a) Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 2.
b) Tập xác định của hàm số \(y = f(x)\) là \(D = \mathbb{R}\backslash {\rm{\{ }}2\} \).
c) Giá trị nhỏ nhất của hàm số bằng 0.
d) Hàm số có hai điểm cực trị.
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\vec a\) và \[\overrightarrow b \] thỏa mãn \(\left| {\overrightarrow a } \right| = 2,\,\,\left| {\overrightarrow b } \right| = 3\) và \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 60^\circ \).
a) \[\overrightarrow a \overrightarrow b = \sqrt 3 \].
b) \(\left| {\overrightarrow a - \overrightarrow b } \right| = 7\)
c) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {19} \).
d) \(\left| {\overrightarrow a - 2\overrightarrow b } \right| = 28\).
Cho hình hộp chữ nhật ABCD.A'B'C'D' có \[AB = x\], \[AD = 1\]. \[\widehat {BA'C} = 30^\circ \]. \(M\) là điểm di chuyển trên đoạn \(BD\).
a) Giá trị lớn nhất của góc giữa hai đường thẳng \(AB'\) và \(BA'\) là \({60^o}\)
b) Giá trị lớn nhất của khoảng cách từ \(M\) đến mặt phẳng \[(ABB'A')\] là \[\sqrt 2 \].
c) Giá trị lớn nhất \[{V_{max}}\] của thể tích khối hộp \[ABCD.A'B'C'D'\]là \[{V_{max}} = \frac{3}{2}\]
d) Giá trị lớn nhất của tan góc giữa đường thẳng \(AB'\) và mặt phẳng \(\left( {BCC'B'} \right)\) không tồn tại.
Lời giải
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một em nhỏ cân nặng \(m = 25\;\)kg trượt trên cầu trượt dài \(3,5\;\)m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ \).
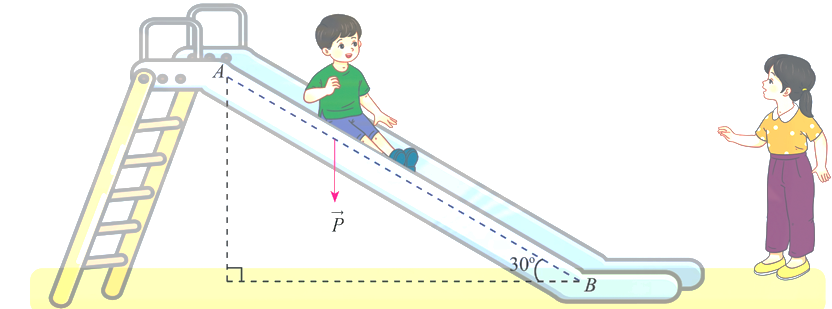
Tính độ lớn của trọng lực \(\vec P = m\vec g\) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\vec g\) có độ lớn là \(g = 9,8\;{\rm{m/}}{{\rm{s}}^2}\). (Làm tròn dến hàng đơn vị)
Một nhà phân tích thị trường làm việc cho một công ty sản xuất thiết bị gia dụng nhận thấy rằng nếu công ty sản xuất và bán \(x\) chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là \(P(x) = - 0,3{x^3} + 36{x^2} + 1800x - 48000.\) Lợi nhuận lớn nhất mà công ty có thể thu được khi sản xuất đúng bao nhiêu chiếc máy xay sinh tố mỗi tháng.
Từ tấm bìa hình vuông có cạnh bằng 6 người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp chữ nhật bằng bao nhiêu ?
Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ \(Oxyz\) được thiết lập như hình vẽ, cho biết \(M\) là vị trí của máy bay, . Biết điểm \(M(a;b;c)\). Tính tổng \(a + 2b + 3c = ...\) (kết quả làm tròn kết quả đến hàng đơn vị)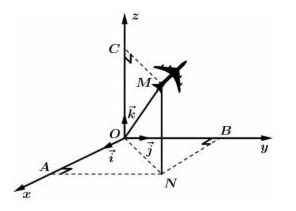
Một bể ban đầu chứa \(150\) lít nước. Sau đó, cứ mỗi phút người ta bơm thêm \(50\) lít nước, đồng thời cho vào bể \(20\) gam chất khử trùng ( hòa tan ). Đặt \(f\left( t \right)\) gam/lít là nồng độ chất khử trùng trong bể sau \(t\) phút ( \(t \ge 0\)), biết rằng sau khi khảo sát sự biến thiên của hàm số \(f\left( t \right)\), ta thấy giá trị \(f\left( t \right)\) tăng theo \(t\) nhưng không vượt ngưỡng \(p\) gam/lít. Tìm số \(p\) ( kết quả thể hiện dưới dạng số thập phân ).
Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ tấm bìa này làm một mô hình kim tự tháp Ai Cập, người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là các cạnh của hình vuông rồi gấp lên và ghép lại thành một hình chóp tứ giác đều. Thể tích của mô hình lớn nhất khi cạnh đáy của mô hình bằng \(\frac{{a\sqrt 2 }}{b}\left( m \right)\,\)(\(a,b \in \mathbb{Z};a,b\)nguyên tố cùng nhau). Tính tổng \({a^2} + {b^2}\)?
![Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ t (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1761639676.png)
