Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 10
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian Oxyz cho \(\overrightarrow a \left( {2;3;6} \right)\). Khi đó độ dài của véctơ \(\overrightarrow a \)là
\(5\).
\(7\).
\(6\).
\( - 7\).
Cho hàm số \(y\, = \,f\left( x \right)\)liên tục trên đoạn \(\left[ { - 2;\,2} \right]\)và có đồ thị dưới đây. Gọi \(M\)và \(m\)lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 2;\,2} \right]\). Giá trị của \(M\, + \,m\)bằng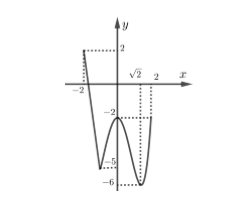
\( - 8\).
\( - 6\).
\( - 4\).
\( - 3\).
Cho hàm số\(y = f\left( x \right)\) có bảng biến thiên như sau: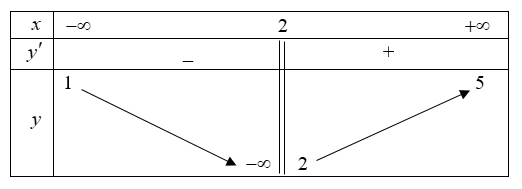
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là
\(0\).
\(3\).
\(1\).
\(2\).
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 25\). Tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \(\left( S \right)\)là
\(I\left( { - 2; - 3;1} \right)\,;\,R = 25\).
\(I\left( {2;3; - 1} \right)\,;\,R = 5\).
\(I\left( { - 2; - 3;1} \right)\,;\,R = 5\).
\(I\left( {2;3; - 1} \right)\,;\,R = 25\).
Trong không gian \[{\rm{Oxyz}}\], hình chiếu vuông góc của điểm \(E\left( {1; - 2;3} \right)\)trên mặt phẳng \(\left( {Oyz} \right)\)có tọa độ là
\[\left( {0;2;3} \right)\].
\[\left( {1;0;0} \right)\].
\[\left( {1; - 2;0} \right)\].
\[\left( {0; - 2;3} \right)\].
Cho hàm số \(y = \frac{{x - 3}}{{x + 3}}\). Khẳng định nào sau đây là khẳng định đúng ?
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 3; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ { - 3} \right\}\).
Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ { - 3} \right\}\).
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 3; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right) = \frac{{ax + 3}}{{2x - b}}\)có bảng biến thiên như sau
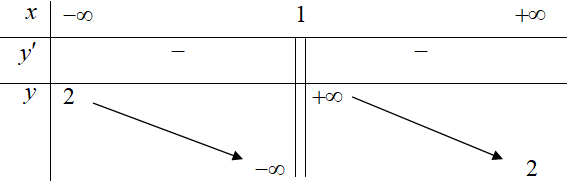
Giá trị \(a - 2b\)bằng?
\( - 6\)
\(8\)
\(0\)
\(10\)
Biết rằng giá trị nhỏ nhất của hàm số \(y = {x^3} + ({m^2} + 1)x + {m^2} - 2\) trên đoạn\(\left[ {0;2} \right]\)bằng 7. Giá trị của tham số \(m\) bằng
\(m = \pm 1\).
\(m = \pm \sqrt 2 \).
\(m = \pm 3\).
\(m = \pm \sqrt 7 \).
Trong không gian với hệ tọa độ Oxyz, cho \(A\left( {1;1;2} \right)\), \(B\left( {2; - 1;1} \right)\) và \(C\left( {3;2; - 3} \right)\). Tìm tọa độ điểm \(D\) để \(ABCD\) là hình bình hành.
\(\left( {0; - 2;6} \right)\).
\[\left( {4;0; - 4} \right)\].
\(\left( {2;4; - 2} \right)\).
\[\left( {4;2; - 4} \right)\].
Cho hình hộp \[ABCD.A'B'C'D'\]. Hệ thức nào đúng?
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AB'} \).
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AA'} \).
Cho hàm số \[y = a{x^4} + b{x^2} + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\] có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?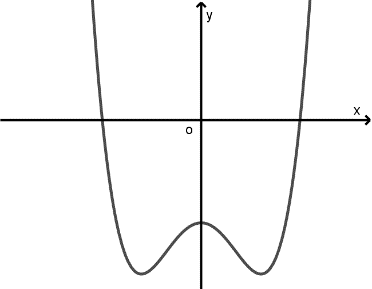 
\[a < 0;\,b > 0;c > 0.\]
\[a < 0;\,b > 0;c < 0.\]
\[a > 0;\,b < 0;c < 0.\]
\[a > 0;\,b > 0;c < 0.\]
Cho hàm số nào \(y = f\left( x \right)\) có \[f'\left( x \right) = {x^2}{\left( {x - 1} \right)^3}\left( {3 - x} \right)\left( {x - 5} \right).\] Số điểm cực tiểu của đồ thị hàm số là
\(3.\)
\(1.\)
\(2.\)
\(4.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f(x)\)có đạo hàm \({y^/} = {f^/}(x) = x{(x - 2)^3},\forall x \in R\). Các mệnh đề sau đúng hay sai?
a) Hàm số \(y = f(x)\) nghịch biến trên khoảng \(( - \infty ;\,1)\).
b) \(f(2024) > f(2025)\).
c) Hàm số \(y = f(x)\) có 2 điểm cực trị.
d) Giá trị nhỏ nhất trên khoảng \[(0; + \infty )\] là \[f(2)\].
Cho hình chóp tứ giác đều \(S.ABCD\) có độ dài tất cả các cạnh đều bằng \(a\).
a) \(\left( {\overrightarrow {SB} ,\overrightarrow {BD} } \right) = {45^ \circ }\)
b) Tam giác\[SBD\] vuông cân tại S.
c) Tứ giác\(ABCD\) là hình vuông.
d) \(\overrightarrow {SB} \cdot \overrightarrow {BD} = - {a^2}.\)
Một người đàn ông muốn chèo thuyền ở vị trí \(A\) tới điểm \(B\) về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng \(3\,\,{\rm{km}}\).
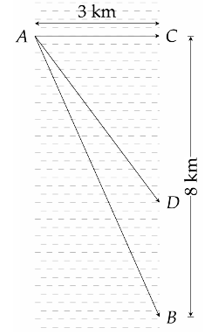
Anh có thể chèo thuyền của mình trực tiếp qua sông để đến \(C\) và sau đó chạy đến \(B\), hay có thể chèo trực tiếp đến \(B\), hoặc anh ta có thể chèo thuyền đến một điểm \(D\) giữa \(C\) và \(B\) và sau đó chạy đến \(B\). Biết anh ấy có thể chèo thuyền \(6\,\,{\rm{km/}}\,{\rm{h}}\), chạy \(8\,\,{\rm{km/}}\,{\rm{h}}\) và quãng đường \(BC = 8\,\,{\rm{km}}\). Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Gọi \(x\,\,\left( {{\rm{km}}} \right)\) là độ dài quãng đường \(BD\). Xét tính đúng sai trong các khẳng định sau:
a) Khoảng \(1\) giờ \(20\) phút là khoảng thời gian ngắn nhất để người đàn ông đến \(B\).
b) \(8 - x\,\,\left( {{\rm{km}}} \right)\)là độ dài quãng đường \(CD\).
c) Tổng thời gian di chuyển từ \(A\) đến \(B\) là \(\frac{{\sqrt {{x^2} + 9} }}{3} + \frac{{8 - x}}{8}\).
d) Thời gian chèo thuyền trên quãng đường \(AD\) là: \(\frac{{\sqrt {{x^2} + 9} }}{3}\).
Cho hàm số \(y = x + \frac{4}{x}\).
a) Đạo hàm của hàm số đã cho là \(y' = 1 + \frac{4}{{{x^2}}}\).
b) Đạo hàm của hàm số đã cho nhận giá trị âm trên các khoảng \(\left( { - 2;\,0} \right) \cup \left( {0;\,2} \right)\) và nhận giá trị dương trên các khoảng \(\left( { - \infty ;\, - 2} \right) \cup \left( {2;\, + \infty } \right)\).
c) Bảng biến thiên của hàm số đã cho là:
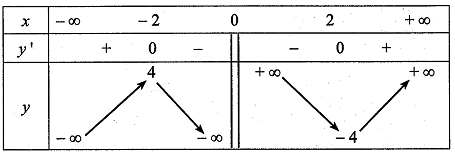
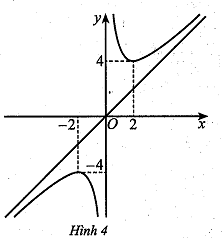
d) Đồ thị hàm số đã cho như ở hình 4
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một lực tĩnh điện \(\vec F\) tác động lên điện tích điểm \(M\) trong điện trường đều làm cho \(M\) dịch chuyển theo đường gấp khúc \(MNP\). Biết \(q = {2.10^{ - 12}}\)(C) và vectơ cường độ điện trường có độ lớn \(E = 1,{8.10^5}\;\)(N/C) và \(d = MH = 5\;\)(mm). Biết công \(A\) sinh bởi lực tĩnh điện \(\vec F\) bằng \(a{.10^{ - 9}}(J)\) Tính a.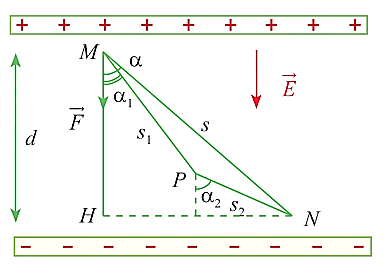
Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu \(EF\) bắc qua sông.Biết rằng thành phố \(A\) cách con sông một khoảng là \(4km\) và thành phố \(B\) cách con sông một khoảng là \(6km\)(hình vẽ), biết \(HE + KF = 20km\) và độ dài \(EF\) không đổi. Hỏi xây cây cầu tại vị trí \(E\)cách thành phố \(A\) là bao nhiêu \(km\) để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường \(AEFB\))? (kết quả làm tròn đến phần trăm).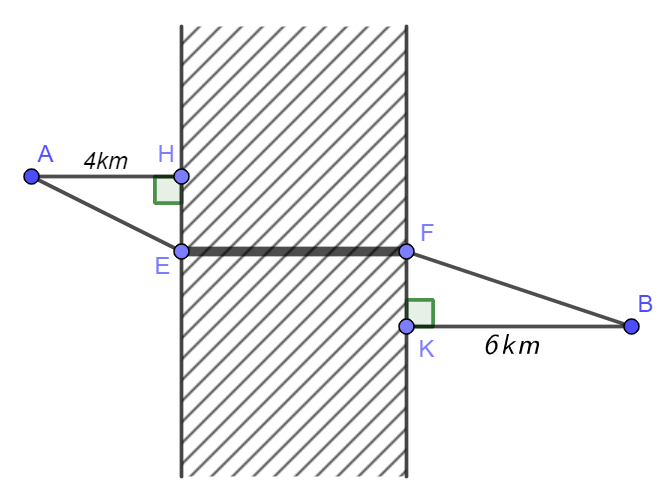
Cho một bờ hồ hình bán nguyệt có bán kính bằng \(2\,\,{\rm{km}}\), đường kính \(PR\)như hình vẽ sau :
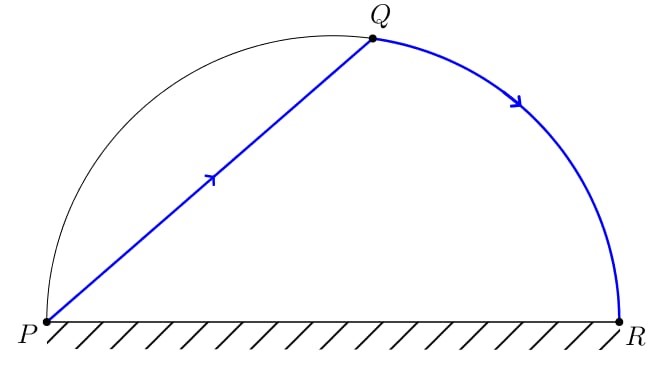
Từ điểm \(P\)anh Tài chèo một chiếc thuyền với vận tốc \(3\,\,{\rm{km/h}}\) đến điểm \(Q\) trên bờ hồ, rồi chạy bộ dọc theo thành hồ đến vị trí \(R\) với vận tốc \(6\,\,{\rm{km/h}}\). Thời gian chậm nhất mà anh Tài di chuyển từ \(P\) đến \(R\) là bao nhiêu? (thời gian tính bằng phút).
Một bồn hình trụ cao \(h\) chứa nước. Theo định luật Torricelli, vận tốc tia nước chảy qua lỗ ở độ sâu \(x\) so với mặt nước là \(V = \sqrt {2gx} \). Người ta cho rằng tầm xa \(R\) (feet) của tia nước được cho bởi \(R = 2\sqrt {x(h - x)} \)Biết lỗ phun nên đặt ở độ cao \(x = K.h,\,(K \in \mathbb{R})\) so với mặt bồn thì tầm xa \(R\) đạt cực đại. Tìm \(K\)?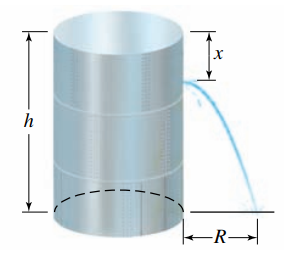
Một bể cá đầy nước có dạng hình hộp chữ nhật ABCD.EFGH với \(AB = 6\) (dm), \(AD = 8\) (dm) và cạnh bên bằng \(10\) (dm). Một chú cá con bơi theo những đoạn thẳng từ điểm \(G\) đến chạm mặt đáy của hồ, rồi từ điểm đó bơi đến vị trí điểm \(M\) là trung điểm của \(AF\) được mô hình hóa như hình vẽ sau:
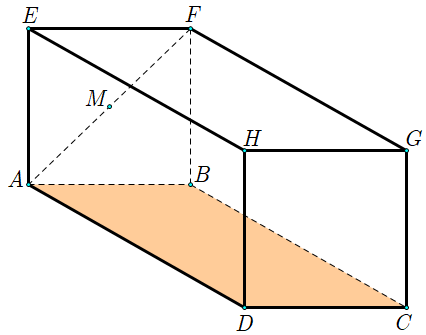
Để đường đi ngắn nhất thì chú cá bơi đến điểm dưới đáy hồ cách \(BA\) và \(BC\) những đoạn bằng \(a\) và \(b.\) Khi đó tổng \(D = 3a + 6b\) bao nhiêu ?
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: \(N(t) = 1000 + \frac{{100t}}{{100 + {t^2}}}({\rm{con}}),\)trong đó \(t\) là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.
