Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 1
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Hàm số \(y = {x^4} - 2{x^2} + 3\) nghịch biến trên khoảng nào?
\(\left( {0;1} \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
\(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
\(\left( { - 1;1} \right)\).
Trong hệ trục tọa độ \[{\rm{Ox}}yz\], cho các điểm \(A\left( {2;1; - 1} \right),B\left( {3;0;1} \right),C\left( {2; - 1;3} \right)\)và điểm \(D\left( {0;8;0} \right)\). Tính thể tích tứ diện \(ABCD\).
\(6\).
\(5\).
\(4\).
\(3\).
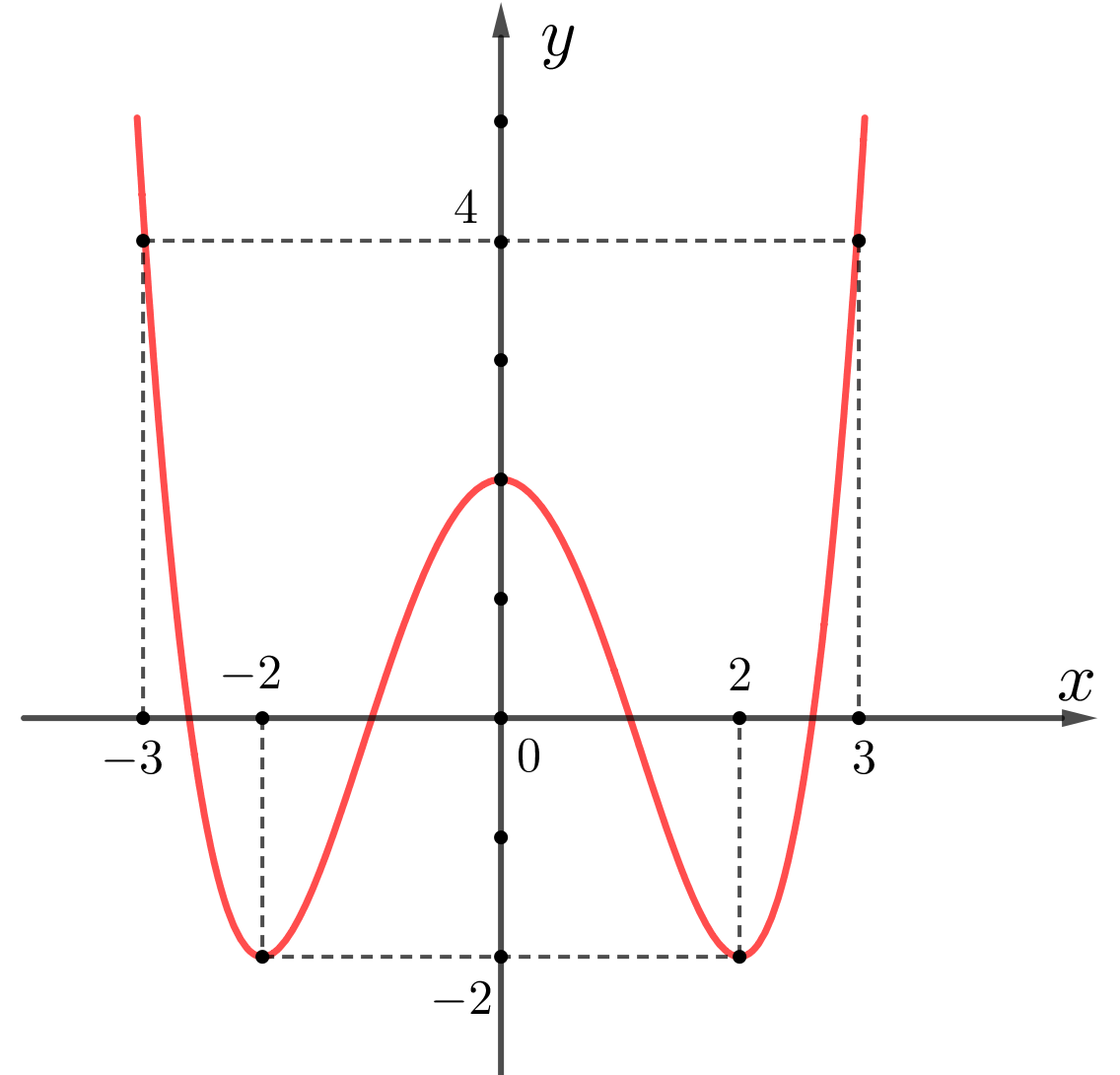
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số này trên đoạn \[\left[ { - 2;3} \right]\] bằng
\(5.\)
\(4.\)
\(3.\)
\(2.\)
Trong không gian với hệ trục toạ độ Oxyz, cho điểm \(A\left( {2;\,2;\,1} \right)\). Tính độ dài đoạn thẳng \(OA\).
\(OA = 3\).
\(OA = 5\).
\(OA = 9\).
\(OA = \sqrt 5 \).
Trong không gian với hệ tọa độ Oxyz, cho điểm \[A\left( {3; - 2;3} \right)\], \[B\left( { - 1;2;5} \right)\], \[C\left( {1;0;1} \right)\]. Tìm tạo độ trọng tâm \[G\] của tam giác \[ABC\]?
\(G\left( {3;0;1} \right)\).
\(G\left( {0;0; - 1} \right)\).
\(G\left( { - 1;0;3} \right)\).
\(G\left( {1;0;3} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên ở hình vẽ.
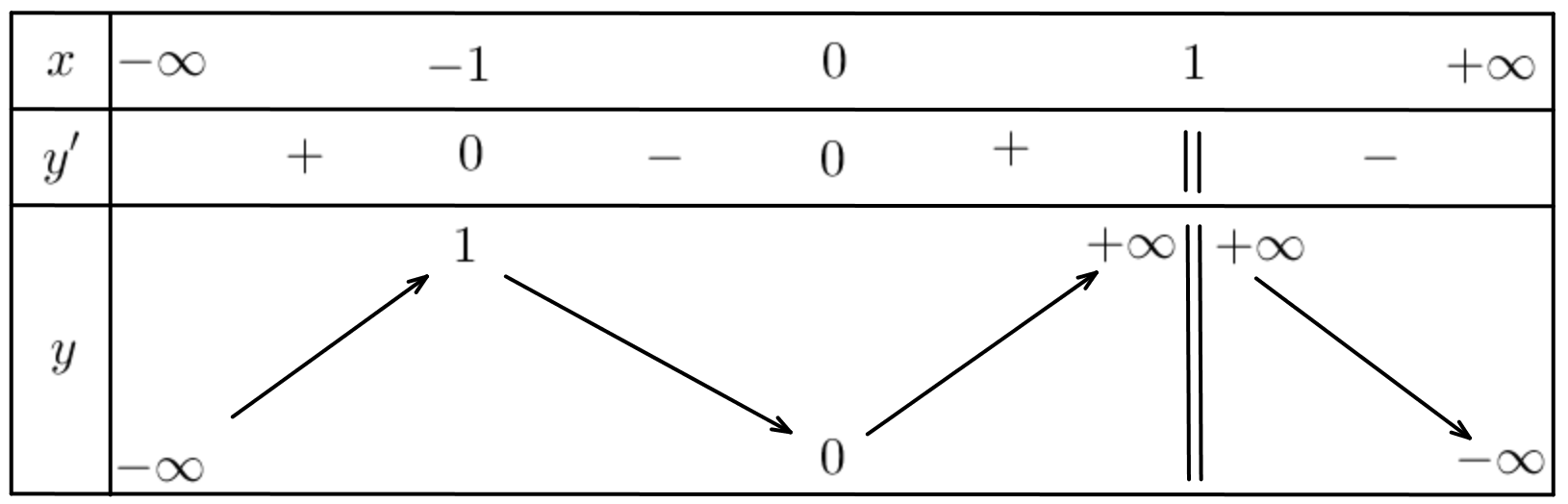
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
\(2\).
\(1\).
\(0\).
\(3\).
Hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và \(f'\left( x \right) = \left| x \right|{\left( {x + 2} \right)^3}\left( {4 - {x^2}} \right)\). Số điểm cực tiểu của hàm số \(y = f\left( x \right)\) là
\[2\].
\[3\].
\[1\].
\[0\].
Tìm tất cả các giá trị thực của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = \frac{{x + 2{m^2} - m}}{{x - 3}}\) trên đoạn \(\left[ {0;1} \right]\) bằng \( - 2\).
\[m = 1\] hoặc \(m = - \frac{1}{2}\).
\[m = 3\] hoặc \(m = - \frac{5}{2}\).
\[m = - 1\] hoặc \(m = \frac{3}{2}\).
\[m = 2\] hoặc \(m = - \frac{3}{2}\).
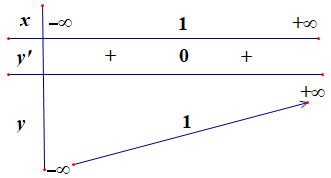
Bảng biến thiên sau đây là của hàm số nào? Chọn 1 câu đúng.
\(y = {x^3} + 3{x^2} + 3x\).
\(y = {x^3} - 3{x^2} + 3x\).
\(y = {x^3} + 3{x^2} - 3x\).
\(y = - {x^3} + 3{x^2} - 3x\).
Cho hàm số \(y = a{x^3} + cx + d\)\(\left( {a \ne 0} \right)\)có \(\mathop {\min }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = f\left( { - 2} \right).\)Giá trị lớn nhất của hàm số \(y = f\left( x \right)\)trên đoạn \(\left[ {1;3} \right]\)bằng
\[8a + d\].
\[d - 16a\].
\[2a + d\].
\[d - 11a\].
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \[A\left( { - 2;3;1} \right)\], \[B\left( {2;1;0} \right)\], \[C\left( { - 3; - 1;1} \right)\]. Tìm tất cả các điểm \[D\] sao cho \[ABCD\] là hình thang có đáy \[AD\] và \[{S_{ABCD}} = 3{S_{ABC}}\].
\[D\left( { - 12; - 1;3} \right)\].
\[\left[ \begin{array}{l}D\left( { - 8; - 7;1} \right)\\D\left( {12;1; - 3} \right)\end{array} \right.\].
\[D\left( {8;7; - 1} \right)\].
\[\left[ \begin{array}{l}D\left( {8;7; - 1} \right)\\D\left( { - 12; - 1;3} \right)\end{array} \right.\].
Cho lăng trụ tam giác ABC.A'B'C' có \[\overrightarrow {AA'} = \overrightarrow a ,\;\,\overrightarrow {AB} = \overrightarrow b ,\;\,\overrightarrow {AC} = \overrightarrow c \]. Hãy phân tích (biểu diễn) véc tơ \[\overrightarrow {BC'} \] qua các véc tơ \[\overrightarrow a ,\,\;\overrightarrow b ,\,\;\overrightarrow c \].
\[\overrightarrow {BC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {BC'} = \overrightarrow a + \overrightarrow b - \overrightarrow c \].
\[\overrightarrow {BC'} = - \overrightarrow a - \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {BC'} = - \overrightarrow a + \overrightarrow b - \overrightarrow c \].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}}\) (1), với \(m\) là số thực.
a) Khi \(m = 1\) đồ thị hàm số có đường tiệm cận xiên là \(y = x - 2\).
b) Khi \(m = 1\) giao điểm của đường tiệm cận xiên và tiệm cận đứng của đồ thị hàm số là \(I\left( {3; - 5} \right)\).
c) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
d) Có 2 giá trị \(m\) để góc giữa hai tiệm cận của đồ thị hàm số (1) bằng \({45^0}\).
Khi nuôi tôm thẻ trong ao, một kỹ sư thủy sản đã thống kê được nếu mỗi mét vuông mặt ao thả \(x\) con tôm giống thì cuối mỗi vụ con tôm có cân nặng trung bình là \(108 - {x^2}\).
a) Để lượng tôm thu được tăng lên thì mật độ tôm giống thả vào ao là từ 6 đến 10 con/\({m^2}\).
b) Sau mỗi vụ khối lượng tôm trung bình trong mỗi mét vuông mặt ao là \(\left( {108 - {x^2}} \right)x\).
c) Khi thả 10 con tôm giống /\({m^2}\) thì lượng tôm thu được là \(0,8\,\,kg/{m^2}\).
d) Để sản lượng tôm lớn nhất thì nên thả 6 con tôm/\({m^2}\).
Trong không gian Oxyz, cho các điểm \(A(4;2; - 1),B(1; - 1;2)\) và \(C(0; - 2;3)\). Xét tính đúng sai của các mệnh đề sau:
a) \(|\overrightarrow {AB} | = 3\sqrt 3 \)
b) Toạ độ điểm \(N\) thuộc mặt phẳng \((Oxy)\), sao cho \(A,B,N\) thẳng hàng là\({\rm{(3; }}1;0)\)
c) Toạ độ điểm \(M\) sao cho \(\overrightarrow {AB} + \overrightarrow {CM} = \vec 0\) là \({\rm{(3; }}1;0)\)
d) \(\overrightarrow {AB} = ( - 3; - 3;3)\)
Cho hàm số \(y = f(x) = {x^3} + 8{x^2} + 5x + 1.\)
a) Đạo hàm \(f'(x) = 3{x^2} + 8x + 5.\)
b) Hai điểm cực trị của đồ thị hàm số nằm cùng phía so với trục \[Oy.\]
c) \(f(0) < f(x)\)với mọi \(x \in \mathbb{R}.\)
d) Hàm số đã cho đồng biến trên khoảng \(\left( { - 1; + \infty } \right).\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một phần đường chạy của tàu lượn siêu tốc (hình 1) khi gắn hệ trục toạ độ \[{\rm{O}}xy\] được mô phỏng ở hình 2, đơn vị trên mỗi trục là mét. Biết đường chạy của nó là một phần đồ thị hàm bậc ba \(y = a{x^3} + b{x^2} + cx + d\,\left( {0 \le x < 90} \right)\); tàu lượn siêu tốc xuất phát từ điểm \(A\), đi qua các điểm \(C,D\) đồng thời đạt độ cao nhỏ nhất so với mặt đất là \(6m\). Độ cao lớn nhất mà tàu lượn siêu tốc đạt được là bao nhiêu mét so với mặt đất? (Kết quả làm tròn đến hàng phần chục).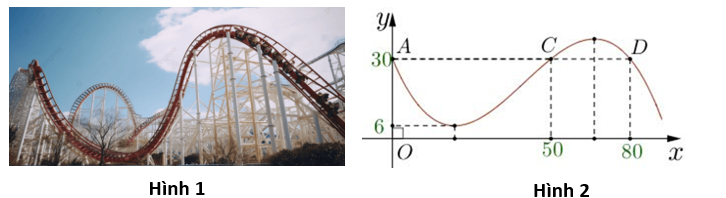
Anh Nam có một mảnh đất rộng và muốn dành ra một khu đất hình chữ nhật có diện tích 200 m2 để trồng vài loại cây mới. Anh dự kiến rào quanh ba cạnh của khu đất hình chữ nhật này bằng lưới thép, cạnh còn lại sẽ tận dụng bức tường có sẵn. Do điều kiện địa lí, chiều rộng khu đất không vượt quá 15 m, hỏi chiều rộng của khu đất này bằng bao nhiêu để tổng chiều dài lưới thép cần dùng là ngắn nhất ?
Một công ty nhận sản xuất 400.000 huy chương bạc nhân ngày kỷ niệm Hội khỏe phù đổng toàn quốc. Công ty sở hữu 20 máy, mỗi máy có thể sản xuất 200 huy chương/giờ. Chi phí lắp đặt máy để sản xuất huy chương là 80 triệu đồng/máy và tổng chi phí vận hành là 5,76 triệu đồng/giờ. Hãy biểu diễn chi phí sản xuât 400.000 huy chương bằng một hàm theo số máy đã dùng. Hãy ước tính số máy mà công ty nên dùng để chi phí thấp nhất.
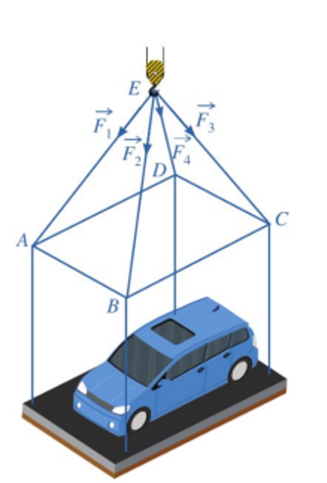
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA,EB,EC,ED\) có độ dài bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \(60^\circ \). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng (làm tròn đến đơn vị nghìn N) của chiếc xe ô tô (làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \), \(\overrightarrow {{F_4}} \) đều có cường độ là \(4700\;N\) và trọng lượng của khung sắt là \(3000\;N\).
Một người đứng ở mặt đất điều khiển hai flycam để phục vụ trong một chương trình của đài truyền hình. Flycam I ở vị trí \(A\) cách vị trí điều khiển \(150\;{\rm{m}}\) về phía nam và \(200\;{\rm{m}}\) về phía đông, đồng thời cách mặt đất \(50\;{\rm{m}}\). Flycam II ở vị trí \(B\) cách vị trí điều khiển \(180\;{\rm{m}}\) về phía bắc và \(240\;{\rm{m}}\) về phía tây, đồng thời cách mặt đất \(60\;{\rm{m}}\). Chọn hệ trục toạ độ \(Oxyz\)với gốc \(O\) là vị trí người điều khiển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\)có hướng trùng với hướng nam, trục \(Oy\)trùng với hướng đông, trục \(Oz\)vuông góc với mặt đất hướng lên bầu trời, đơn vị trên mỗi trục tính theo mét. Khoảng cách giữa hai flycam đó bằng bao nhiêu mét ( làm tròn đến hàng đơn vị)?
Lợi nhuận tổng hàng ngày (tính theo đô la) mà TKK Corporation thu được từ việc sản xuất và bán \(x\) đĩa DVD có thể ghi lại được cho bởi hàm lợi nhuận \(P(x) = - 0,000001{x^3} + 0,001{x^2} + 5x - 500;\quad 0 \le x \le 2000\). Tìm mức sản xuất \(x\) để lợi nhuận hàng ngày đạt cực đại. (làm tròn kết quả đến hàng đơn vị)