Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 6
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một tứ giác lồi. Hình chóp \(S.ABCD\)có tất cả bao nhiêu mặt?
\(4\).
\(3\).
\(6\).
\(5\).
Mệnh đề nào sau đây đúng với mọi số nguyên \(k\)
\[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi + \alpha + k2\pi \end{array} \right.\].
\[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\].
\[\sin x = \sin \alpha \Leftrightarrow \left\{ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\].
Cho hai đường thẳng chéo nhau a và b . Lấy A,B thuộc a và C,D thuộc b . Khẳng định nào sau đây đúng khi nói về hai đường thẳng AD và BC ?
Chéo nhau.
Cắt nhau.
Song song nhau.
Có thể song song hoặc cắt nhau.
Công thức nào sau đây là đúng với một cấp số cộng có số hạng đầu \({u_1}\), công sai \(d\) và số tự nhiên \(n \ge 2\)
\({u_n} = {u_1} + \left( {n - 1} \right)d\).
\({u_n} = {u_1} - \left( {n - 1} \right)d\).
\({u_n} = {u_1} + \left( {n + 1} \right)d\).
\({u_n} = {u_1} + d\).
Góc có số đo \(108^\circ \) đổi ta rađian là
\(\frac{{3\pi }}{5}\).
\(\frac{\pi }{4}\).
\(\frac{{3\pi }}{2}\).
\(\frac{\pi }{{10}}\).
Đẳng thức nào sau đây Sai?
\[\cos 2a = 2{\cos ^2}a - 1\].
\[\cos 2a = {\cos ^2}a - {\sin ^2}a\].
\[\cos 2a = 1 - 2{\sin ^2}a\].
\[\cos 2a = 2.\sin a.cosa\].
Trong các đẳng thức sau, đẳng thức nào đúng?
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{{{{\left( { - 1} \right)}^n}}}{{{u_n}}}\end{array} \right.\). Số hạng \({u_4}\) bằng
\(2\).
\( - 2\).
\( - \frac{1}{2}\).
\(\frac{1}{2}\).
Tập xác định của hàm số \(y = \frac{{2\cos x - 1}}{{\sin 2x}}\) là:
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ { \pm \frac{\pi }{3} + k2\pi ;\frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\).
Cho tứ diện \[ABCD\] có \[M,\,\,N\] lần lượt là trung điểm của \[BC\] và \[CD.\] Gọi \[K\] là điểm tuỳ ý thuộc miền trong tam giác \[ABD.\] Giao tuyến của \[\left( {KMN} \right)\] và \[\left( {ABD} \right)\] có tính chất là:
Song song với \[BD.\]
Cắt cạnh \[AC.\]
Chứa trong \[\left( {ACD} \right).\]
Cắt cạnh \[BD.\]
Cho tứ diện \(ABCD\)có \(M\), \(N\)lần lượt là trung điểm của \(AB\), \(CD\)và \(P\)là một điểm thuộc cạnh \(BC\)(\(P\) không là trung điểm của \(BC\)). Thiết diện của tứ diện bị cắt bởi mặt phẳng \(\left( {MNP} \right)\)là
Lục giá
Tứ giá
Ngũ giá
Tam giá
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là \(12288{\rm{ }}{{\rm{m}}^2}\)). Tính diện tích mặt trên cùng.
\(10{m^2}\).
\(12{m^2}\).
\(8{m^2}\).
\(6{m^2}\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là tứ giác không có cạnh nào song song với nhau. Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(M\) là điểm thuộc miền trong của tam giác \(SAB\), \(I\) là giao điểm của \(AB\) và \(CD\).
a) Giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\) là đường thẳng \(SM\).
b) Nếu \(BC\parallel AD\) thì giao tuyến của hai mặt phẳng \((MBC)\) và \((SAD)\) là đường thẳng \(d\) song song với \(AD\) và đi qua điểm \(M\).
c) Điểm \(I\) là một điểm chung của hai mặt phẳng \((SAC)\) và \((SBD)\).
d) Giao tuyến của hai mặt phẳng \((SAC)\) và \((SBD)\) là đường thẳng \(SO\).
Xét tính đúng sai của các khẳng định sau.
a) Tập xác định của hàm số \(y = \tan \left( {2x - \frac{\pi }{3}} \right)\) là \(\mathbb{R} \setminus \left\{ {\frac{{5\pi }}{{12}} + k\pi ,k \in \mathbb{Z}} \right\}\).
b) Tập xác định của hàm số \(y = \sin 2x\) là \(\mathbb{R}\).
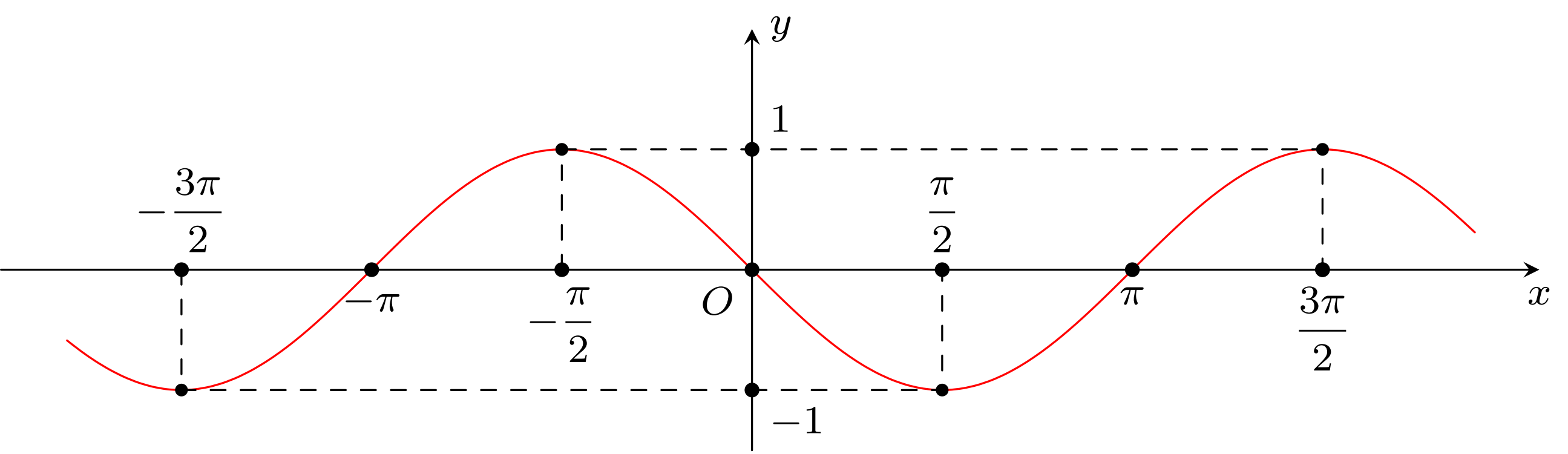
c) Đường cong trong hình dưới là đồ thị của hàm số \(y = \sin x\)
d) Giá trị lớn nhất của hàm số \(y = {\sin ^2}x - \cos x + 2\) là \(3\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm thu/huyết áp tâm trương,tương ứng. Chỉ số huyết áp \[120/80\] là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số

\[P\left( t \right) = 110 + 10\sin \left( {\frac{{5\pi }}{2}t} \right)\].
Trong đó \[P\left( t \right)\] là huyết áp tính theo đơn vị \[{\rm{mmHg}}\] (milimét thủy ngân) và thời gian \[t\] tính theo giây.Hỏi trong khoảng từ \(0\)đến \(5\)giây có bao nhiêu lần huyết áp là \[120\] mmHg?
Bạn An là sinh viên của một trường đại học, muốn vay tiền ngân hàng với lãi suất ưu đãi để trang trải kinh phí học tập. Đầu năm thứ nhất, bạn ấy vay ngân hàng số tiền 40 triệu đồng với lãi suất là \(4\% \) một năm. Tính số tiền mà bạn An nợ ngân hàng sau 4 năm, biết rằng trong 4 năm đó bạn An chưa trả bất kì khoản nào và lãi suất ngân hàng không thay đổi.
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Tìm \(m\) để phương trình để \(2{\sin ^2}\frac{x}{2} + \sqrt 3 \sin x - 5m = 0\) luôn có nghiệm.
Cho hình chóp tứ giác S.ABCD với đáy ACBD có các cạnh đối diện không song song với nhau và M là một điểm trên cạnh SA. Tìm giao điểm của đường thẳng SB với mặt phẳng (MCD) .
Thành phố X muốn thi công xây dựng cây thông noel đặt ở trung tâm thành phố. Giá thi công tầng thứ nhất là \(2\) triệu đồng, tầng tiếp theo tăng \(500\) ngàn đồng và cứ tiếp tục như vậy cho đến tầng \(81\). Hỏi thành phố X phải trả chi phí thi công là bao nhiêu?








