Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 5
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Giải phương trình \(\sin 3x = \sin x\) ta được tập nghiệm của phương trình là
\(\left\{ {k\pi ,k \in \mathbb{Z};\frac{\pi }{4} + l\frac{\pi }{2}\,,\,l \in \mathbb{Z}} \right\}\).
\(\left\{ {k2\pi \,,\, k \in \mathbb{Z}} \right\}\).
\(\left\{ {\frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(\left\{ {\frac{\pi }{4} + k\pi \,,\,k \in \mathbb{Z}} \right\}\).
Cho hai đường thẳng phân biệt \[a\] và \[b\] trong không gian. Có bao nhiêu vị trí tương đối giữa \[a\] và \[b\]?
\(2\)
\(4\)
\(3\)
\(1\)
Ba số \(a,b,c\)theo thứ tự lập thành một cấp số cộng khi và chỉ khi
\(a + c = 2b\).
\(ac = {b^2}\).
\(bc = {a^2}\).
\(b + c = 2a\).
Khẳng định nào dưới đây sai?
\(\sin 2a = 2\sin a\cos a\).
\(2{\sin ^2}a = 1 - \cos 2a\).
\(\cos 2a = 2\cos a - 1\).
\(\sin \left( {a + b} \right) = \sin a\cos b + \sin b\cos a\).
Tập xác định của hàm số \(y = \frac{1}{{2\cos x - 1}}\)là
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{3} + k2\pi ,\frac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\]
\[\left\{ {\frac{\pi }{3} + k2\pi ,\frac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\]
\(D = \mathbb{R}\backslash \left\{ {\frac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\)
Chọn khẳng định SAI.
Qua ba điểm phân biệt xác định được một và chỉ một mặt phẳng.
Qua 2 đường thẳng phân biệt cắt nhau xác định được một và chỉ một mặt phẳng.
Qua một đường thẳng và một điểm nằm ngoài đường thẳng xác định được một và chỉ một mặt phẳng.
Qua 2 đường thẳng phân biệt và song song xác định được một và chỉ một mặt phẳng.
Cho dãy số \(\left( {{U_n}} \right)\) có số hạng tổng quát \({U_n} = \frac{{n - 1}}{{n + 2}},\left( {n \in {N^*}} \right)\). Số hạng thứ \(100\) của dãy số là
\({U_{100}} = \frac{{33}}{{34}}.\)
\({U_{100}} = \frac{{39}}{{34}}.\)
\({U_{100}} = \frac{{37}}{{34}}.\)
\({U_{100}} = \frac{{35}}{{34}}.\)
Chọn khẳng định đúng.
\(\cot \left( {\pi - \alpha } \right) = \cot \alpha \).
\(\tan \left( {\pi - \alpha } \right) = \tan \alpha \).
\(\cos \left( {\pi - \alpha } \right) = - \cos \alpha \).
\(\sin \left( {\pi - \alpha } \right) = - \sin \alpha \).
Cung có số đo \[250^\circ \] thì có số đo theo đơn vị radian là:
\[\frac{{25\pi }}{{12}}\].
\[\frac{{25\pi }}{9}\].
\[\frac{{25\pi }}{{18}}\].
\[\frac{{35\pi }}{{18}}\].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang Gọi \(M,N\) lần lượt là trung điểm \(SB,SC.\) Khi đó mặt phẳng \(\left( {AMN} \right)\) cắt hình chóp \(S.ABCD\) theo thiết diện là
ngũ giác.
tam giác.
hình thang.
tứ giác.
Cho hình chóp \(S.ABCD,\,ABCD\) là hình bình hành ( tham khảo hình vẽ). Tìm giao tuyến của hai mặt phẳng \((SAD)\)và \((SBC)\).
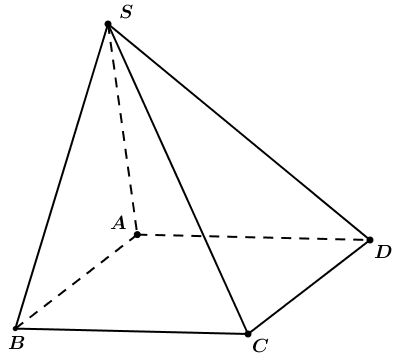
Giao tuyến của hai mặt phẳng \((SAD)\)và \((SBC)\)là đường thẳng \(d\)đi qua \(S\)và song song với \(AB\).
Giao tuyến của hai mặt phẳng \((SAD)\)và \((SBC)\)là đường thẳng \(SE\) với \(E\)là giao điểm của \(AC\)và \(BC\).
Giao tuyến của hai mặt phẳng \((SAD)\)và \((SBC)\)là đường thẳng \(SE\) với \(E\)là giao điểm của \(AD\)và \(BD\).
Giao tuyến của hai mặt phẳng \((SAD)\)và \((SBC)\)là đường thẳng \(d\)đi qua \(S\)và song song với \(AD\).
Sinh nhật bạn của An vào ngày \[01\] tháng năm. An muốn mua một món quà sinh nhật cho bạn nên quyết định bỏ ống heo \[100\] đồng vào ngày \[01\] tháng \[01\] năm \[2016\], sau đó cứ liên tục ngày sau hơn ngày trước \[100\] đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền ? (thời gian bỏ ống heo tính từ ngày \[01\] tháng \[01\] năm \[2016\] đến ngày \[30\] tháng \[4\] năm \[2016\]) .
\(726.000\) đồng.
\(750.300\) đồng.
\(738.100\) đồng.
\(714.000\) đồng.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho các hàm số \(f(x) = \sqrt {3 - 2\sin x} \); và \(g(x) = \tan \frac{x}{2} - \frac{1}{3}\cos x\). Xét tính đúng sai của các khẳng định sau.
a) Hàm số \(f(x)\) đã cho là hàm tuần hoàn.
b) Hàm số \(f(x)\) có tập xác định là \(\mathcal{D} = \mathbb{R}\).
c) Hàm số \(g(x)\) xác định khi \(x \ne k2\pi (k \in \mathbb{Z})\).
d) Hàm số \(g(x)\) đã cho là hàm không tuần hoàn.
Cho biết tính đúng sai của mỗi phát biểu sau
a) Hai mặt phẳng phân biệt không cắt nhau thì song song.
b) Nếu mặt phẳng này chứa hai đường thẳng cùng song song với mặt phẳng kia thì hai mặt phẳng đó song song với nhau.
c) Hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau.
d) Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Một du khách vào trường đua ngựa đặt cược, lần đầu đặt 100 000 đồng, mỗi lần sau, tiền đặt cược gấp đôi số tiền cược trước đó. Người đó thua 5 lần liên tiếp tính từ lần đặt cược đầu tiên và thắng ở lần thứ 6 (số tiền nhận được khi thắng bằng 2 lần số tiền đã đặt cược ở lần chơi đó). Hỏi số tiền (nghìn đồng) du khách trên đã thắng hay thua là bao nhiêu sau 6 lần chơi?
Học sinh An tiến hành làm một thí nghiệm trên một con lắc đơn. Tại vị trí cân bằng, An tác động một lực lên con lắc theo phương ngang. Từ các kết quả thí nghiệm cho thấy, An tính được con lắc dao động điều hòa quanh vị trí cân bằng theo phương trình \(s = 2\sqrt 2 \cos \left( {7t + \frac{\pi }{3}} \right)\) với \(s\)(\(cm\)) là độ dài cung quét của con lắc từ một vị trí bất kì tại thời điểm \(t\) (giây) đến vị trí cân bằng. Con lắc đi qua vị trí cân bằng bao nhiêu lần trong khoảng thời gian từ \(0\)đến \(30\) giây?

PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Cho tứ giác \[ABCD\] có \[AC\] và \[BD\] giao nhau tại \[O\] và một điểm \[S\] không thuộc mặt phẳng\[\left( {ABCD} \right)\]. Trên đoạn \[SC\] lấy một điểm \[M\] không trùng với \[S\] và \[C\]. Xác định giao điểm của đường thẳng \[SD\] với mặt phẳng \[\left( {ABM} \right).\]
Công ty \(A\) đề xuất \(2\) phương án trả lương để người lao động chọn như sau:
Phương án 1: Người lao động sẽ nhận \(45.000.000\)đồng cho năm làm việc đầu tiên và kể từ năm thứ hai, mức lương sẽ tăng thêm \(3.000.000\) đồng so với năm trước đó.
Phương án 2: Người lao động sẽ nhận mức lương \(7.000.000\)đồng cho qúy làm việc đầu và kể từ qúy thứ hai mức lương sẽ tăng thêm \(500.000\) đồng so với qúy trước đó.
Hỏi sau \(10\) năm số tiền lương mà người lao động nhận được theo mỗi phương án là bao nhiêu?
Số giờ có ánh sáng của thành phố \(T\) ở vĩ độ 40o bắc trong ngày thứ \(t\) của một năm không nhuận được cho bởi hàm số \(d(t) = 3 \cdot \sin \left[ {\frac{\pi }{{182}}(t - 80)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\). Bạn An muốn đi tham quan thành phố \(T\) nhưng lại không thích ánh sáng mặt trời, vậy bạn An nên chọn đi vào ngày nào trong năm để thành phố \(T\) có ít giờ có ánh sáng mặt trời nhất?








