Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 4
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Góc 18o có số đo bằng rađian là bao nhiêu?
\(\frac{\pi }{{10}}\).
\(\frac{\pi }{{360}}\).
\(\pi \).
\(\frac{\pi }{{18}}\).
Các dãy số có số hạng tổng quát \({u_n}\). Trong các dãy số sau, dãy số nào không phải là cấp số cộng?
\(49\), \(43\),\(37\), \(31\), \(25\).
\({u_n} = 1 + {3^n}\).
\({u_n} = {\left( {n + 3} \right)^2} - {n^2}\).
\({u_n} = 2n + 5\).
Tập xác định của hàm số \(y = \frac{{2\sin x - 1}}{{\cos x}}\) là
\(D = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Trong không gian cho hai đường thẳng a và b cắt nhau. Đường thẳng c cắt hai đường thẳng a và Có bao nhiêu mệnh đề sai trong các mệnh đề sau?
I) a, b, c luôn đồng phẳng.
II) a, b đồng phẳng.
III) a, c đồng phẳng.
2.
3.
0.
1.
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = - 1,\,\,{u_2} = 3\,\\{u_{n + 1}} = {u_n} + 2{u_{n - 1}}\end{array} \right.\,\) với \(n \ge 2\). Tìm 5 số hạng đầu của dãy.
\( - 1,\,3,\,1,\,7,\,9\).
\( - 1,\,3,\,5,\,13,\,31\).
\( - 1,\,3,\,2,\,5,\,7\).
\( - 1,\,3,\,5,\, - 1,\, - 11\).
Mệnh đề nào sau đây sai?
\(\cos 2a = {\cos ^{2{\rm{ }}}}a - {\sin ^2}a\).
\(\cos 2a = {\sin ^{2{\rm{ }}}}a - {\cos ^2}a\)
\(\cos 2a = 2{\cos ^2}a - 1\).
\(\cos 2a = 1 - 2{\sin ^2}a\).
Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
\(\sin \alpha = - \sin \beta \).
\(\tan \alpha = - \tan \beta .\)
\(\cos \alpha = - \cos \beta .\)
\(\cot \alpha = - \cot \beta .\)
Nghiệm của phương trình \(\sin 2x = 1\) là.
\(x = \frac{\pi }{2} + k2\pi \).
\(x = \frac{\pi }{4} + k\pi \).
\(x = \frac{{k\pi }}{2}\).
\(x = \frac{\pi }{4} + k2\pi \).
Cho hai đường thẳng \(a\) và \(b\). Điều kiện đủ để kết luận \(a\) và \(b\)chéo nhau là
\(a\) và \(b\)là 2 cạnh của 1 tứ diện.
\(a\) và \(b\)không có điểm chung.
\(a\) và \(b\)không cùng nằm trên \(1\) mặt phẳng bất kì.
\(a\) và \(b\)nằm trên 2 mp phân biệt.
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của cạnh \(AC,AD;G\) là trọng tâm của tam giác \(BCD\). Khi đó giao tuyến của \(\left( {BMN} \right)\) và \(\left( {GCD} \right)\) là
đường thẳng \(BG\).
đường thẳng \(d\) đi qua \(B\) và \(d\)//\(CD\).
đường thẳng \(d\) đi qua \(G\) và \(d\)//\(CD\).
đường thẳng \(BK\) với \(K = MN \cap CD\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I\), \(J\) lần lượt là trung điểm \(SB\) và \(SD\). Thiết diện của mặt phẳng \(\left( {AIJ} \right)\) với hình chóp \(S.ABCD\) là 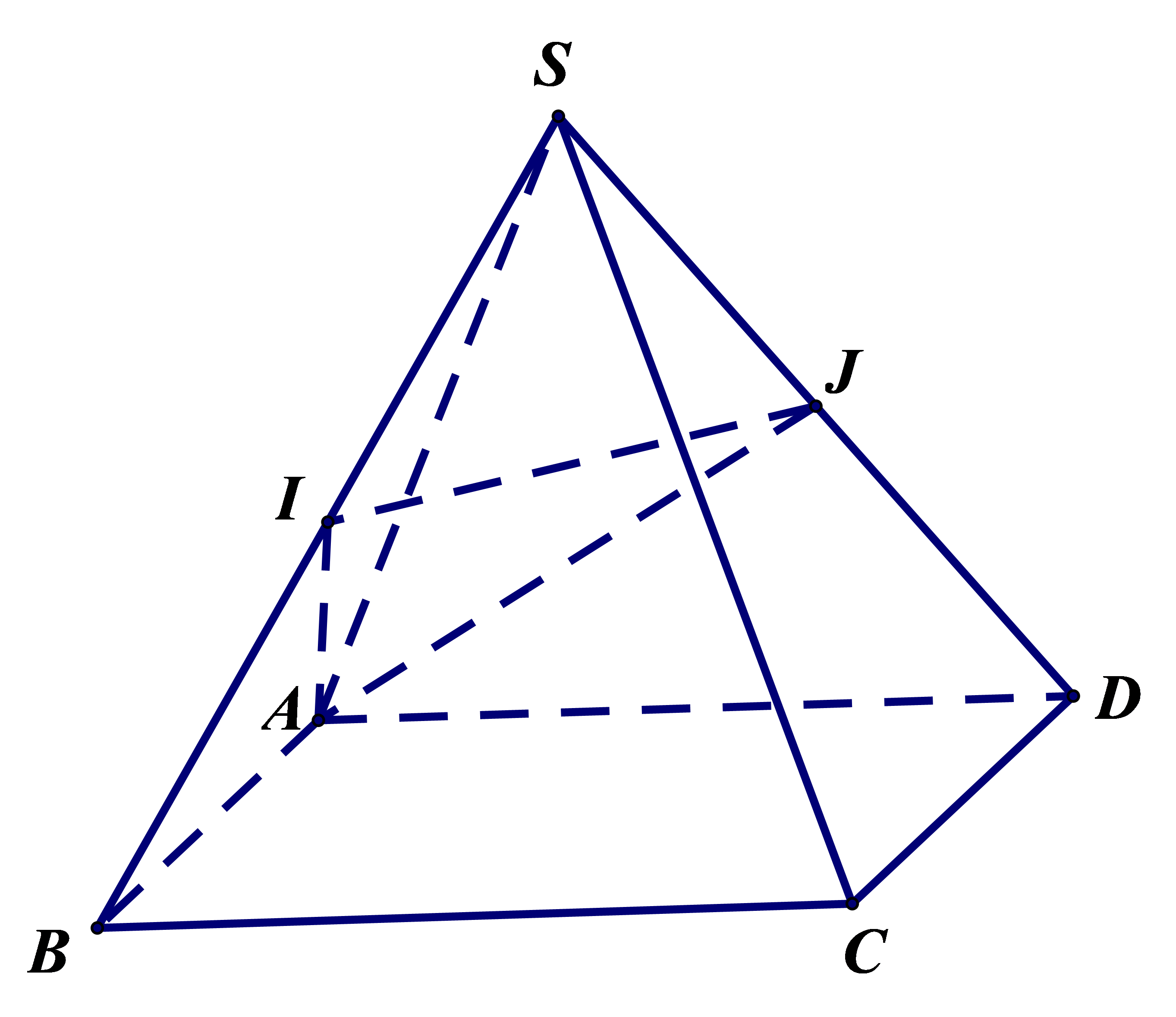
tứ giác.
tam giác.
lục giác.
ngũ giác.
Một bể nước có dung tích \(1000\) lít. Người ta mở vòi cho nước chảy vào bể, ban đầu bể cạn nước. Trong một giờ đầu vận tốc nước chảy vào bể là \(1\) lít/\(1\) phút. Trong các giờ tiếp theo vận tốc nước chảy giờ sau gấp đôi giờ liền trước. Hỏi sau khoảng thời gian bao lâu thì bể đầy nước (kết quả gần đúng nhất )?
\[3,14\] giờ.
\[4,64\] giờ.
\[4,14\] giờ.
\[3,64\] giờ.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Xét tính đúng sai của các khẳng định sau.
a) \(\cos x = 1 \Leftrightarrow x = k\pi (k \in \mathbb{Z})\).
b) \(\sin x = 0 \Leftrightarrow x = k2\pi (k \in \mathbb{Z})\).
c) \(\tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k2\pi (k \in \mathbb{Z})\).
d) \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k\pi (k \in \mathbb{Z})\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SC\). Cho biết tính đúng, sai của mỗi phát biểu sau:
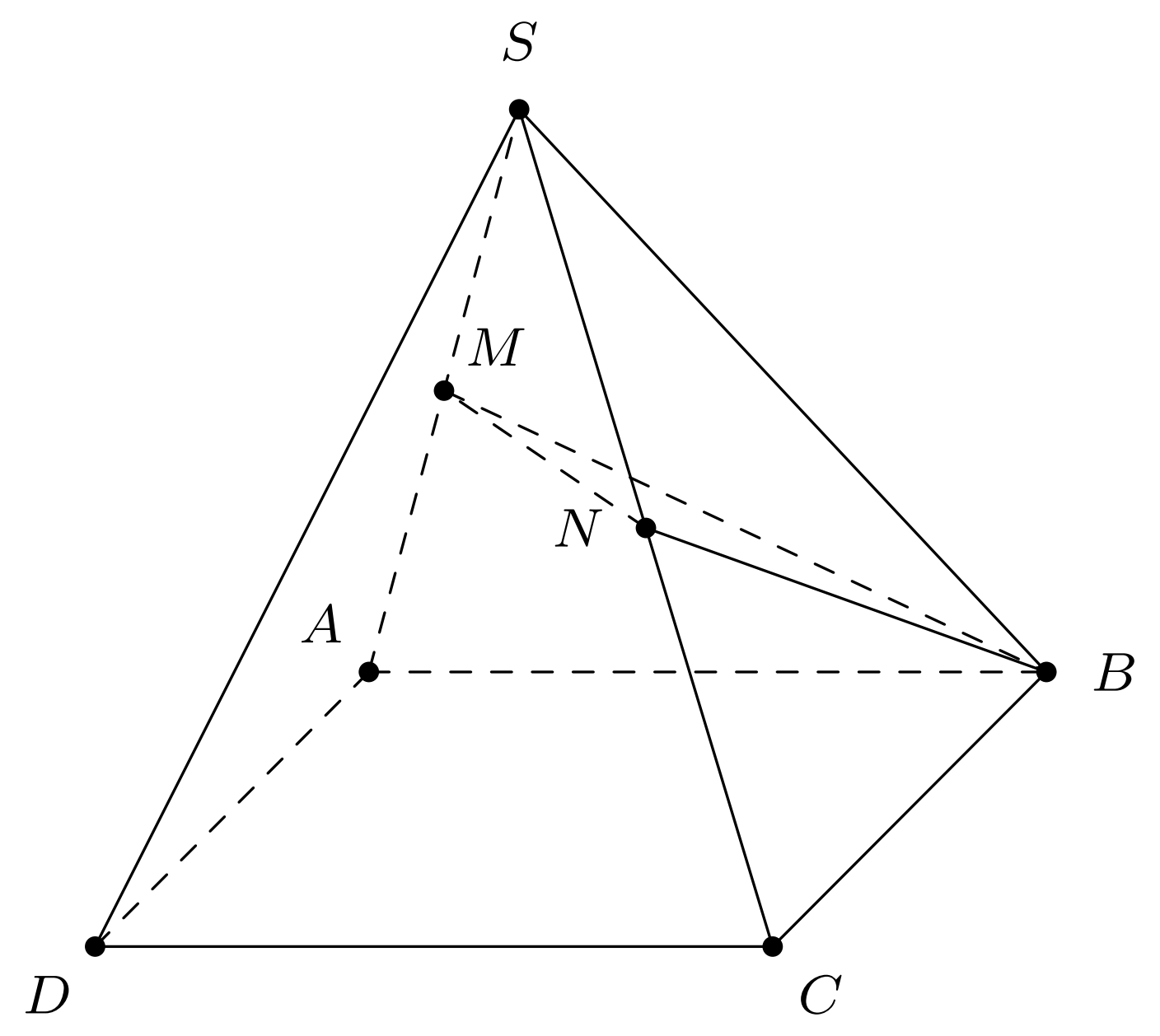
a) Thiết diện của hình chóp khi cắt bởi mặt phẳng \((MNB)\) là một hình thang.
b) Đường thẳng \(MN\) song song với đường thẳng \(BD\).
c) Giao tuyến của mặt phẳng \((MNB)\) và mặt phẳng \((ABCD)\) là một đường thẳng đi qua \(B\) và song song với \(AC\).
d) Gọi \(O\) là tâm hình bình hành \(ABCD\). Giao tuyến của \((MNB)\) và \((SBD)\) là đường thẳng đi qua \(B\) và trung điểm của đoạn \(SO\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Người ta dự định xây dựng 1 tòa tháp 10 tầng tại một ngôi chùa nọ, theo cấu trúc diện tích của mặt sàn tầng trên bằng nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là \(16{m^2}\). Hãy giúp nhà chùa ước lượng số gạch hoa cần dùng để lát nền nhà. Để cho đồng bộ các nhà chùa yêu cầu nền nhà phải lót gạch hoa cỡ \(30 \times 30cm\). (làm tròn đến hàng đơn vị).
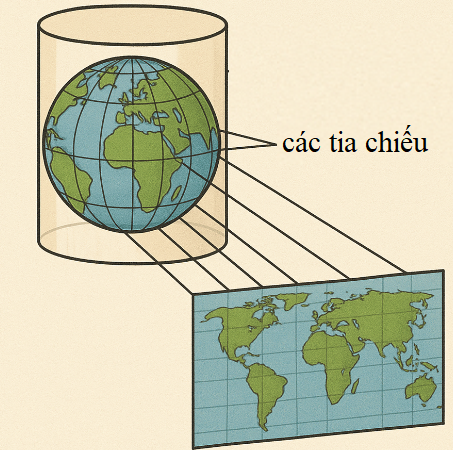
Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 9. Trên bản đồ phẳng lấy đường xích đạo làm trực hoành và kinh tuyến \({0^0}\)làm trục tung. Khi đó tung độ của một điểm có vĩ độ \({\varphi ^0}( - 90 < \varphi < 90)\)được cho bởi hàm số \(y = 30\tan (\frac{\pi }{{180}}\varphi )\,(cm)\). Sử dụng đồ thị hàm số tang, Biết điểm ở vĩ độ dương lớn nhất là \({A^0}\) nằm cách xích đạo không quá \(30\,cm\)trên bản đồ. Tìm \(A\)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Hai chiếc tàu thủy cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc . Tàu thứ nhất chạy với tốc độ \(20\) km/h, tàu thứ hai chạy với tốc độ \(30\) km/h. Hỏi sau \(3\) giờ hai tàu cách nhau bao nhiêu km?
Có tất cả bao nhiêu giá trị nguyên của \(m\) để phương trình \(\cos \left( {2x - \frac{\pi }{3}} \right) = \frac{1}{2}m - 1\) có nghiệm?
Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của SB, SD; Tìm giao điểm của SC và mặt phẳng (AMN).








