Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 3
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phương trình \[\sin x = \frac{{\sqrt 3 }}{2}\] có nghiệm là
\[x = \pm \frac{\pi }{3} + k2\pi \].
\[\left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = \frac{{5\pi }}{6} + k\pi \end{array} \right.\].
\[\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\].
\[x = \frac{\pi }{3} + k\pi \].
Trong các dãy số sau, dãy nào là 1 cấp số cộng?
\(1,3,5,8,10\).
\(2,5,8,11,14\).
\(2, - 4,8, - 16,32\).
\(1,5,3,6,9\).
Chọn khẳng định sai trong các khẳng định sau
\(\cos 2a = 2{\cos ^2}a - 1\) .
\(\cos 2a = 1 - 2{\sin ^2}a\) .
\(\cos 2a = 1 - 2{\cos ^2}a\) .
\(\cos 2a = {\cos ^2}a - {\sin ^2}a\) .
Số đo góc \(105^\circ \)đổi sang rađian bằng
\(\frac{{9\pi }}{{12}}\).
\(\frac{{7\pi }}{{12}}\).
\[\frac{{5\pi }}{{12}}\].
\(\frac{{5\pi }}{8}\).
Cho hai đường thẳng phân biệt \(a,b\) và mặt phẳng \(\left( \alpha \right)\). Giả sử \(a{\rm{//}}\left( \alpha \right),\,\,b \subset \left( \alpha \right)\). Khi đó
\(a,\,\,b\) chéo nhau.
\(a,\,\,b\) cắt nhau.
\(a{\rm{//}}b\) hoặc \(a,\,\,b\) chéo nhau.
\(a{\rm{//}}b\).
Trong các đẳng thức sau, đẳng thức nào đúng?
\[\tan 150^\circ = - \frac{1}{{\sqrt 3 }}\].
\[\cot 150^\circ = \sqrt 3 \].
\[\cos 150^\circ = \frac{{\sqrt 3 }}{2}\].
\[\sin 150^\circ = - \frac{{\sqrt 3 }}{2}\].
Tập xác định của hàm số \(y = \sin \frac{x}{{2019}}\)là
\(\mathbb{Z}\).
\(\mathbb{R}\).
\(\mathbb{R}\backslash \left\{ {2019} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{1}{{2019}}} \right\}\).
Chọn khẳng định sai.
Qua hai đường thẳng phân biệt cắt nhau xác định được một và chỉ một mặt phẳng.
Qua ba điểm phân biệt xác định được một và chỉ một mặt phẳng.
Qua hai đường thẳng song song xác định được một và chỉ một mặt phẳng.
Qua một đường thẳng và một điểm nằm ngoài đường thẳng xác định được một và chỉ một mặt phẳng.
Cho dãy số\(\left( {{u_n}} \right)\) với \({u_n} = n\left[ {1 + {{\left( { - 1} \right)}^n}} \right]\). Số hạng \({u_7}\) bằng
\[0\].
\( - 14\).
\[7\].
\[14\].
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là đường thẳng song song với đường thẳng nào sau đây?
\(AC\).
\(AD\).
\(BD\).
\(SC\).
Cho hình chóp tứ giác \(S.ABCD\) và một mặt phẳng \(\left( P \right)\) thay đổi. Thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\) là một đa giác có số cạnh nhiều nhất có thể là:
\(5\) cạnh.
\(4\) cạnh.
\(3\) cạnh.
\(6\) cạnh.
Cho hình vuông \(ABCD\) có cạnh bằng \(a\) và có diện tích \({S_1}\). Nối bốn trung điểm \({A_1},{B_1},{C_1},{D_1}\) theo thứ tự của bốn cạnh \(AB,BC,CD,DA\) ta được hình vuông thứ hai có diện tích \({S_2}\). Tiếp tục làm như thế, ta được hình vuông thứ ba là \({A_2}{B_2}{C_2}{D_2}\) có diện tích là \({S_3}\), … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích \({S_4},{S_5},...,{S_{100}}\) (hình vẽ)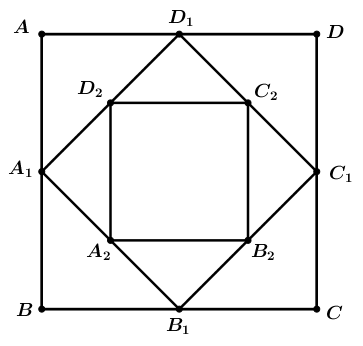
Biết tổng \({S_1} + {S_2} + {S_3} + ... + {S_{100}} = \frac{{{2^{100}} - 1}}{{{2^{93}}}}\). Tính a?
\(a = 8\)
\(a = 4\)
\(a = 2\)
\(a = 1\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình lượng giác \(2\sin x = \sqrt 2 \), khi đó:
a) Số nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là hai nghiệm
b) Phương trình tương đương \(\sin x = \sin \frac{\pi }{4}\)
c) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{\pi }{4}\)
d) Phương trình có nghiệm là: \(x = \frac{\pi }{3} + k2\pi ;x = \frac{{3\pi }}{4} + k2\pi (k \in \mathbb{Z})\).
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm tam giác \(ABD\), \(M\) là điểm thuộc cạnh \(AB\) sao cho \(AM = 2MB\), \(N\) là trung điểm \(CD\) (tham khảo hình vẽ bên dưới). a) \(MN\)và \(AC\) cắt nhau. b) \(CG\)và \(AD\) cắt nhau. c) \(GM\parallel (BCD)\). d) \(D \in (GMN)\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Giả sử vật giao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\). Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng cm. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần? ( hình ảnh minh họa vị trí cân bằng)
Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây an toàn có tính đàn hồi kéo nảy ngược lên \(60{\rm{\% }}\) chiều sâu của cú nhảy. Một người chơi bungee thực hiện củ nhảy đầu tiên có độ cao nảy ngược lên là \(9{\rm{\;m}}\). Tính tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu. (Kết quả làm tròn hàng phần chục)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(O\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(SB\), \(SD\) và \(OC\). Gọi giao điểm của \(\left( {MNP} \right)\) với \(SA\) là \(K\). Tỉ số \(\frac{{KS}}{{KA}} = \frac{m}{n}\), với \(m\), \(n \in \mathbb{Z}\) và \(\left( {m,n} \right) = 1\). Tính \(m + n\).
Khán đài A của một sân vận động có \(3456\) chỗ ngồi, hàng ghế đầu tiên có \(15\) chỗ ngồi và mỗi hàng ghế sau có thêm \(6\) chỗ so với hàng ghế ngay trước nó. Hỏi khán đài A của sân vận động có bao nhiêu hàng ghế?
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số 
, với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc và chiết xuất của hai môi trường. Biết rằng khi góc tới bằng 45o thì góc khúc xạ bằng 30o. Khi góc tới là 60o thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.
