Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 19
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tam giác \(ABC\) có ba góc \(A,\,B,\,C\)thỏa mãn đẳng thức \(\sin A = \cos B + \cos C\). Khẳng định nào sau đây là khẳng định đúng?
Tam giác \(ABC\) là tam giác đều.
Tam giác \(ABC\) vuông cân tại \(A\).
Tam giác \(ABC\) vuông tại \(B\) hoặc \(C\).
Tam giác \(ABC\)vuông tại \(B\).
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy \(A,\,\,B\) thuộc \(a\) và \(C,\,\,D\) thuộc \(b\). Khẳng định nào sau đây đúng khi nói về hai đường thẳng \(AD\) và \(BC\)?
Song song nhau.
Chéo nhau.
Có thể song song hoặc cắt nhau.
Cắt nhau.
Tập xác định của hàm số \(y = \tan \left( {2x - \frac{\pi }{3}} \right)\) là
\(\mathbb{R}\backslash \left\{ {\frac{{5\pi }}{6} + k\pi } \right\}\), \(k \in \mathbb{Z}\).
\(\mathbb{R}\backslash \left\{ {\frac{{5\pi }}{{12}} + k\pi } \right\}\), \(k \in \mathbb{Z}\).
\(\mathbb{R}\backslash \left\{ {\frac{{5\pi }}{{12}} + k\frac{\pi }{2}} \right\}\), \(k \in \mathbb{Z}\).
\(\mathbb{R}\backslash \left\{ {\frac{{5\pi }}{6} + k\frac{\pi }{2}} \right\}\), \(k \in \mathbb{Z}\).
Trong các công thức sau, công thức nào đúng?
\(\sin 2a = 2\sin a\cos a\).
\[\sin 2a = {\cos ^2}a - {\sin ^2}a\].
\(\sin 2a = \sin a + \cos a\).
\(\sin 2a = 2\sin a\).
Tìm nghiệm của phương trình \(2\sin x - 3 = 0\).
\(x \in \emptyset \).
\(x \in \mathbb{R}\).
\(\left[ \begin{array}{l}x = \arcsin \left( {\frac{3}{2}} \right) + k2\pi \\x = \pi - \arcsin \left( {\frac{3}{2}} \right) + k2\pi \end{array} \right.\;\left( {k \in \mathbb{Z}} \right)\).
\(\left[ \begin{array}{l}x = \arcsin \left( {\frac{3}{2}} \right) + k2\pi \\x = - \arcsin \left( {\frac{3}{2}} \right) + k2\pi \end{array} \right.\;\left( {k \in \mathbb{Z}} \right)\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = {\left( { - 1} \right)^{n + 1}}\sqrt {n + 1} \). Mệnh đề nào sau đây đúng?
\({u_8} = 3\).
\({u_8} = - 3\).
\({u_8} = \sqrt 8 \).
\({u_8} = - \sqrt 8 \).
Dãy số nào sau đây là cấp số cộng?
\(1;\, - 3;\,9;\, - 27;\,81\) .
\(1;\, - 1;\,1;\, - 1;\,1\) .
\[1;\,2;\,3;\,4;5\].
\(1;\,2;\,4;\,8;\,16\) .
Cho 3 đường thẳng \({d_1},{d_2},{d_3}\) không cùng thuộc một mặt phẳng và cắt nhau từng đôi. Khẳng định nào sau đây đúng
3 đường thẳng trên chứa 3 cạnh của một tam giác.
3 đường thẳng trên trùng nhau.
3 đường thẳng trên đồng quy.
Các khẳng định ở A, B, C đều sai.
Cho hình chóp \[S.ABCD\]có đáy \[ABCD\]là hình bình hành tâm \[O\], \[I\]là trung điểm cạnh \[SC\]. Khẳng định nào sau đây SAI?
\[\left( {IBD} \right) \cap \left( {SAC} \right) = IO\].
\[IO{\rm{// mp}}\left( {SAB} \right)\].
\[{\rm{mp}}\left( {IBD} \right)\]cắt hình chóp \[S.ABCD\]theo thiết diện là một tứ giá
\[IO{\rm{ // mp}}\left( {SAD} \right)\].
Cho hình chóp \(S.ABCD\)có đáy là hình thang với các cạnh đáy là \(AB\)và\(CD\). Gọi \(I,J\)lần lượt là trung điểm của \(AD\)và \(BC\)và \(G\)là trọng tâm tam giác\(SAB\). Giao tuyến của \(\left( {SAB} \right)\)và \(\left( {IJG} \right)\)là
\(SC\).
đường thẳng qua \(G\) và cắt\(BC\).
đường thẳng qua \(G\) và song song với\(CD\).
đường thẳng qua \(S\)và song song với\(AB\).
Cho một hình tròn tâm \(O\) bán kính là \(R = 60m\). Dựng tam giác đều \({A_1}{B_1}{C_1}\) nội tiếp đường tròn, sau đó lấy đường tròn nội tiếp tam giác \({A_1}{B_1}{C_1}\). Cứ tiếp tục làm quá trình như trên. Diện tích của tam giác \({A_9}{B_9}{C_9}\) là 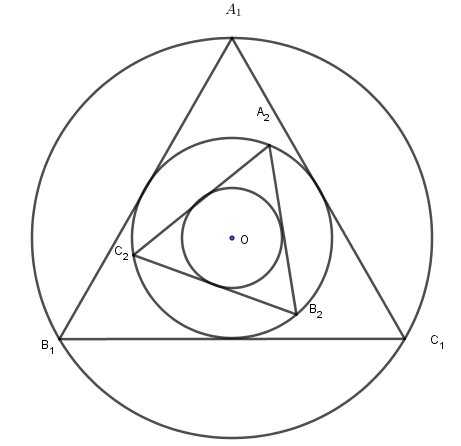
\(0,071{m^2}\) .
\(1,14{m^2}\) .
\(0,285{m^2}\) .
\(145,92{m^2}\) .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({G_1}\), \({G_2}\) là trọng tâm của các tam giác \(A'BD\), \(B'D'C\). Các mệnh đề sau đúng hay sai?
a) Đường thẳng \(A'B\) cắt đường thẳng \(CD\).
b) \(A'D'CB\)là hình bình hành.
c) \(\left( {A'BD} \right)\parallel \left( {B'D'C} \right)\).
d) \({G_1}{G_2} = \frac{2}{3}AC'\).
Cho phương trình \(\left( {2\sin x - 1} \right)\left( {\cos x + 1} \right) = 0\). Xét tính đúng sai của các khẳng định sau.
a) \(x = \frac{\pi }{6}\)là một nghiệm của phương trình.
b) Nghiệm âm lớn nhất của phương trình là \(x = \frac{{ - 7\pi }}{6}\).
c) Phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + k2\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \pi + k2\pi }\end{array}} \right.\).
d) Tổng các nghiệm của phương trình thuộc nửa khoảng \(\left[ { - 2\pi ;3\pi } \right)\) bằng \(3\pi \).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình \(x = 5\cos \left( {4t - \frac{\pi }{3}} \right)\) trong đó \(t\) là thời gian tính bằng giây và \(x\) là quãng đường tính bằng centimet. Hãy cho biết, trong khoảng 10 giây đầu tiên, vật đi qua vị trí cân bằng bao nhiêu lần.
Bác An gửi tiết kiệm vào ngân hàng 100 triệu đồng với hình thức lãi kép tức là số tiền lãi cộng vào tiền gốc và tiếp tục sinh lãi, kì hạn một năm với lãi suất \(4,7\% \)/năm. Tính số tiền cả gốc và lãi bằng bao nhiêu triệu đồng mà bác An nhận được sau 10 năm. (Giả sử lãi suất không thay đổi trong suốt thời gian gửi tiền). Làm tròn kết quả đến hàng đơn vị
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Một kiến trúc sư thiết kế một hội trường với \(9\) ghế ở hàng thứ nhất, \(12\) ghế ở hàng thứ hai, \(15\) ghế ở hàng thứ ba, và cứ như vậy số ghế hàng sau hơn số ghế hàng trước là \(3\). Nếu muốn hội trường có sức chứa ít nhất \(561\) ghế ngồi thì kiến trúc sư đó phải thiết kế ít nhất bao nhiêu hàng ghế?
Cho phương trình \(4\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 8\left( {{{\sin }^6}x + {{\cos }^6}x} \right) - 4{\sin ^2}4x = m\) trong đó \(m\) là tham số. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình có nghiệm?
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành . Gọi \[M\] là trung điểm của \[SB\], \[N\] là trọng tâm \[\Delta SCD\]. Xác định giao điểm của \[MN\] và \[\left( {ABCD} \right)\]








