Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 18
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các phát biểu sau, phát biểu nào đúng?
Hình tứ diện có 6 mặt.
Hình tứ diện có 6 đỉnh.
Hình tứ diện có 4 cạnh.
Hình tứ diện có 4 mặt.
Tìm mệnh đề đúng trong các mệnh đề sau:
Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau.
Hai đường thẳng phân biệt không song song thì chéo nhau.
Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
Số đo radian của góc \(135^\circ \) là
\(\frac{\pi }{2}\).
\(\frac{{3\pi }}{4}\).
\(\frac{{2\pi }}{3}\).
\(\frac{\pi }{6}\).
Tập \(D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2}\left| {k \in \mathbb{Z}} \right.} \right\}\) là tập xác định của hàm số nào sau đây?
\(y = \tan 2x\)
\(y = \cot 2x\).
\(y = \cot x\).
\(y = \tan x\).
Khẳng định nào dưới đây sai? (giả thiết các biểu thức có nghĩa).
\(\cos \left( { - a} \right) = \cos a\).
\(\tan \left( { - a} \right) = \tan a\).
\(\sin \left( { - a} \right) = - \sin a\).
\(\cot \left( { - a} \right) = - \cot a\).
Cho dãy số vô hạn \(\left\{ {{u_n}} \right\}\)là cấp số cộng có công sai \(d\), số hạng đầu \({u_1}\). Hãy chọn khẳng định sai?
\({u_n} = {u_1} + (n - 1).d\), \(\forall n \in {\mathbb{N}^*}\).
\({u_n} = {u_{n - 1}} + d\), \(n \ge 2\).
\({S_{12}} = \frac{n}{2}\left( {2{u_1} + 11d} \right)\).
\({u_5} = \frac{{{u_1} + {u_9}}}{2}\).
Tìm khẳng định Sai:
\({\cos ^2}x = \frac{{1 + \cos 2x}}{2}\).
\(1 + \cos 4x = 2{\cos ^2}2x\).
\(\cos x = {\sin ^2}\frac{x}{2} - {\cos ^2}\frac{x}{2}\).
\(\sin 2x = 2\sin x\cos x\).
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{1}{3}\left( {{u_n} + 1} \right)\end{array} \right.\). Tìm số hạng \({u_4}\).
\({u_4} = 1\).
\({u_4} = \frac{5}{9}\).
\({u_4} = \frac{{14}}{{27}}\).
\({u_4} = \frac{2}{3}\).
Nghiệm của phương trình \[\sin x = - 1\] là:
\[x = - \frac{\pi }{2} + k\pi \].
\[x = - \frac{\pi }{2} + k2\pi \].
\[x = k\pi \].
\[x = \frac{\pi }{6} + k\pi \].
Cho tứ diện \(ABCD\). Gọi \(H,K\) lần lượt là trung điểm các cạnh\(AB,AC\). Trên đường thẳng \(CD\) lấy điểm \(M\) nằm ngoài đoạn \(CD\). Thiết diện của tứ diện với mặt phẳng \((HKM)\) là
Tứ giác \(HKMN\) với \(N \in AD\).
Tam giác \(HKL\) với \(L = KM \cap AD\).
Tam giác \(HKL\) với \(L = HM \cap AD\).
Hình thang \(HKMN\) với \(N \in AD\) và \(HK//MN\).
Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình bình hành. Gọi \(I,J\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD.\) Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng song song với
\(AD\).
\(BJ\).
\(BI\).
\[IJ\].
Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có \[10\] tầng thì bạn An cần đúng bao nhiêu que diêm?
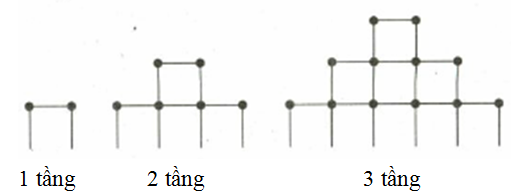
\(270\).
\(100\).
\(210\).
\(39\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho lăng trụ tam giác \(ABC.A'B'C'\) có \(I\), \(K\), \(G\) lần lượt là trọng tâm các tam giác \(ABC\), \(A'B'C'\), \(ACC'\).
a) \((ABC)\parallel \left( {A'B'C'} \right)\).
b) \(IG\)cắt \(\left( {BCC'B'} \right)\).
c) \((IKG)\parallel \left( {BCC'B'} \right)\).
d) \(BB'\parallel \left( {ACC'A'} \right)\).
Cho phương trình \(\sin 2x = m\). Xét tính đúng sai của các khẳng định sau.
a) Với \(m = 0\), phương trình có nghiệm là \(x = \frac{{k\pi }}{4}\).
b) Phương trình có một nghiệm trên \(\left( {0;\frac{\pi }{2}} \right)\) khi \(m \in (0;1)\).
c) Phương trình có nghiệm khi \(m \in [ - 1;1]\).
d) Phương trình có nghiệm là \(x = \frac{\pi }{3}\) khi \(m = \frac{{\sqrt 3 }}{2}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Để tích lũy tiền cho việc học đại học của con gái, cô Thảo quyết định hằng tháng bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi \(0,5{\rm{\% }}\) cộng dồn hằng tháng. Cô bắt đầu chương trình tích luỹ này khi con gái cô tròn 4 tuổi. Cô ấy sẽ tích luỹ được bao nhiêu tiền vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Thảo bao nhiêu tuổi?
Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ):
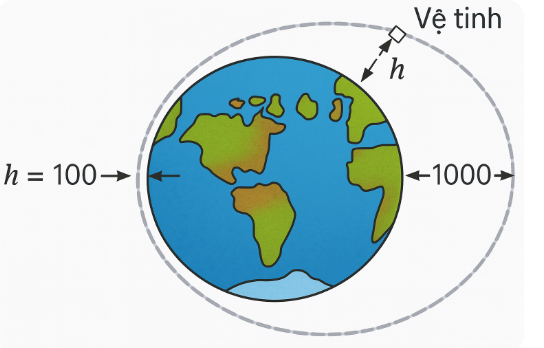
Độ cao \(h\) (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức \(h = 550 + 450 \cdot \cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right)\). Trong đó \(t\) là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người ta cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất xa nhất trong khoảng 120 phút đầu tiên kể từ lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm để có thể thực hiện thí nghiệm đó? (làm tròn kết quả đến hàng phần chục theo đơn vị phút).
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Người ta trồng \(3003\) cây theo một hình tam giác như sau: hàng thứ nhất trồng \(1\) cây, hàng thứ hai trồng \(2\) cây, hàng thứ ba trồng \(3\) cây, \( \ldots \) Cứ như thế, số cây ở hàng sau nhiều hơn hàng kề trước \(1\) cây. Hỏi có tất cả bao nhiêu hàng cây được trồng?
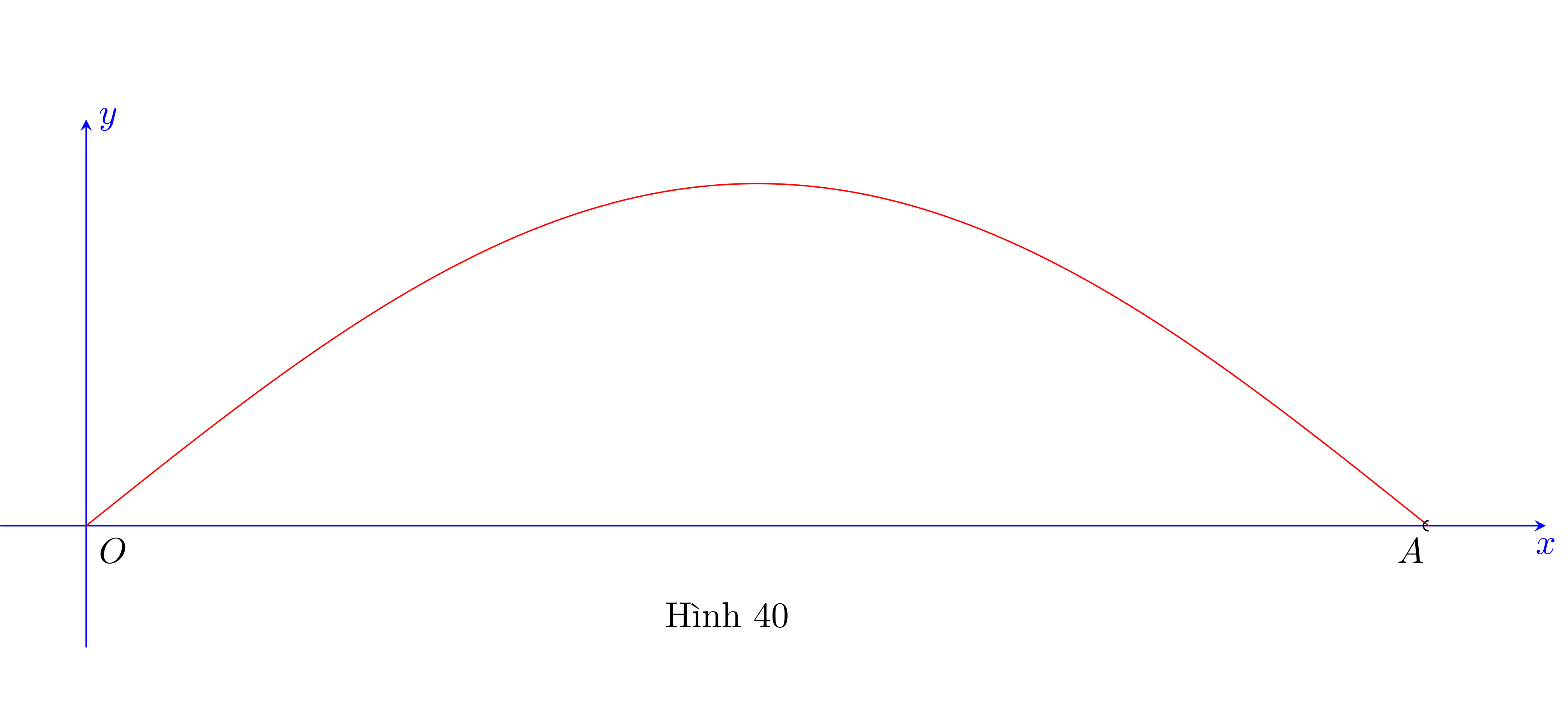
Một cây cầu có dạng cung \(OA\) của đồ thị hàm số \(y = 4,8 \cdot \sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét.
Cho hình chóp tứ giác SABCD với đáy ABCD có các cạnh đối diện không song song với nhau và M là một điểm trên cạnh SA. Tìm giao điểm của đường thẳng MC và mặt phẳng (SBD)








