Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 17
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phương trình \(2\sin x - 1 = 0\)có bao nhiêu nghiệm \(x \in \left( {0;2\pi } \right)\)?
1 nghiệm.
Vô số nghiệm.
2 nghiệm.
4 nghiệm.
Góc \(\frac{\pi }{{18}}\)có số đo bằng độ là:
\({18^0}\).
\({10^0}\).
\({12^0}\).
\({36^0}\).
Trong các mệnh đề sau, mệnh đề nào sai
\(\cos 30^\circ = \sin 120^\circ \).
\[\cos 60^\circ = \sin 30^\circ \].
\(\sin 60^\circ = - \cos 120^\circ \).
\(\cos 60^\circ = \sin 120^\circ \).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {3^n}.\) Tính \({u_{n + 1}}?\)
\({u_{n + 1}} = {3^n} + 3.\)
\({u_{n + 1}} = {3.3^n}.\)
\({u_{n + 1}} = 3\left( {n + 1} \right).\)
\({u_{n + 1}} = {3^n} + 1.\)
Dãy số nào sau đây là một cấp số cộng ?
\(\left( {{u_n}} \right):\,\)\(1\); \(3\); \(6\); \(10\); \(15\); \( \ldots \).
\(\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{c}}{{u_1} = 3}\\{{u_{n + 1}} = 2{u_n} + 1,\,\,\forall n \ge 1}\end{array}} \right.\).
\(\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_{n + 1}} = {u_n} + 2,\,\,\forall n \ge 1}\end{array}} \right.\).
\(\left( {{u_n}} \right):\,\)\( - 1\); \(1\); \( - 1\); \(1\); \( - 1\); \( \ldots \).
Khẳng định nào sau đây đúng?
Hai đường thẳng song song nhau khi chúng ở trên cùng một mặt phẳng.
Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
Hai đường thẳng chéo nhau khi chúng không có điểm chung.
Trong các đẳng thức sau, đẳng thức nào sai?
\(\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a - b} \right) - \sin \left( {a + b} \right)} \right]\).
\(\sin a.\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\).
\(\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) + \cos \left( {a + b} \right)} \right]\).
\(\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a - b} \right) + \sin \left( {a + b} \right)} \right]\).
Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
\(4\).
\(2\).
\(3\).
\(6\).
Điều kiện xác định của hàm số \(y = \frac{{1 - \sin x}}{{\cos x}}\)là
\(x \ne k\pi \).
\(x \ne \frac{\pi }{2} + k\pi \).
\(x \ne - \frac{\pi }{2} + k2\pi \).
\(x \ne \frac{\pi }{2} + k2\pi \).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNP) là
Tứ giác.
Tam giác.
Lục giác.
Ngũ giác.
Cho tứ diện ABCD, gọi I, J, K lần lượt là trung điểm của AC, BC, BGiao tuyến của hai mặt phẳng (ABD) và (IJK) là:
Đường thẳng qua I song song với AD
Đường thẳng qua K song song với AB
Đường thẳng qua J song song với AC
Đường thẳng qua J song song với CD
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của để tháp (có diện tích là 12 288 m2). Tính diện tích mặt trên cùng.
\(12{m^2}\).
\(6{m^2}\).
\(8{m^2}\).
\(10{m^2}\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình lượng giác \(2\cos x = \sqrt 3 \), khi đó:
a) Phương trình có nghiệm \(x = \pm \frac{\pi }{3} + k2\pi (k \in \mathbb{Z})\)
b) Trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) phương trình có nghiệm lớn nhất bằng \(\frac{{13\pi }}{6}\)
c) Trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) phương trình có 4 nghiệm
d) Tổng các nghiệm của phương trình trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) bằng \(\frac{{25\pi }}{6}\)
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD;M,N\) lần lượt là trung điểm của \(SB,SD;P\) thuộc đọan \(SC\) và không là trung điểm của \(SC\).Khi đó:
a) Giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \((MNP)\) là giao điểm của \(MN\) và \(SO\).
b) Giao điểm \(Q\) đường thẳng \(SA\) và mặt phẳng \((MNP)\) là giao điểm của \(PE\) và \(SO\).
c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB,QP\) và \(AC,QN\) và \(AD\). Vậy \(I,J,K\) không thẳng hàng.
d) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB,QP\) và \(AC,QN\) và \(AD\). Vậy \(I,J,K\) thẳng hàng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Số giờ nắng gắt của tỉnh Quảng Nam ở vĩ độ \(40^\circ \) bắc trong ngày thứ \(n\) của một năm không nhuận được cho bởi hàm số: \(f\left( n \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] + 12\), \(n \in \mathbb{Z}\) và \(0 < n \le 365\). Vào ngày thứ bao nhiêu trong năm đó thì tỉnh Quảng Nam chịu nhiều giờ nắng gắt nhất?
Cho hình vuông \({A_1}\) có cạnh bằng \(1\). Gọi \({A_2}\) là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông \({A_1}\); \({A_3}\) là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông \({A_2}\);…Cứ tiếp tục quá trình như trên ta được dãy các hình vuông \({A_1};\,{A_2};\,...;\,{A_n};...\)Tính diện tích của hình vuông \({A_{2024}}\) là \(\frac{1}{{{2^m}}}\). Tìm \(m\)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (tham khảo hình vẽ). Nghiên cứu trò chơi này, người ta thấy khoảng cách \(h\) (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian \(t(s)\) (với \(t \ge 0\)) vởi hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\), trong đó ta quy ước \(d > 0\) khi vị trí cân bằng ở phía sau lưng người chơi đu và \(d < 0\) trong trường hợp ngược lại (Nguồn: Đại số và giải tích 11 Nâng cao, NXBGD Việt Nam, 2022). Vào thời điểm \(t\) nào thì khoảng cách \(h\) là \(3\) m; \(0\) m?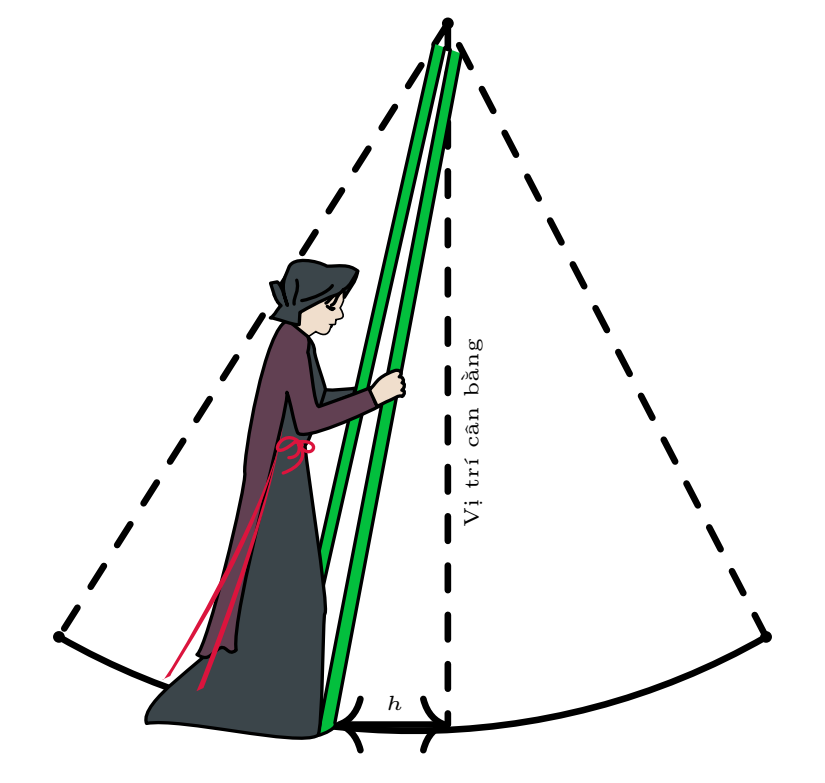
Cho tứ diện \(SABC\). Trên đoạn \(SC\) lấy điểm \(M\) sao cho \(3SM = 2MC\). Gọi \(N\), \(K\) lần lượt là trung điểm của các cạnh \(BC\), \(SA\). Gọi \(I\) là giao điểm của đường thẳng \(AB\) và mặt phẳng \(\left( {KMN} \right)\). Biết \(AB = 2\sqrt 3 \). Độ dài cạnh \(IA\) bằng bao nhiêu? (Làm tròn kết quả đến hai chữ số thập phân)
Chu vi của một đa giác bằng \(158\) cm; các cạnh của đa giác lập thành một cấp số cộng với công sai \(3\) cm. Biết cạnh dài nhất là \(44\) cm. Số cạnh của đa giác đó bằng








