Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 14
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_n} = {n^2} - n + 1\). Số \(91\) là số hạng thứ mấy của dãy?
\[6\].
\[4\].
\[10\].
\[7\].
Phương trình \[\sin x = 1\]có một nghiệm là
\[x = \pi \].
\[x = \frac{\pi }{3}\].
\[x = - \frac{\pi }{2}\].
\[x = \frac{\pi }{2}\].
Cho \(\sin \alpha = \frac{3}{4}\). Tính \(\cos 2\alpha \).
\( - \frac{1}{8}\).
\(\frac{1}{8}\).
\( - \frac{{\sqrt 7 }}{4}\).
\(\frac{{\sqrt 7 }}{4}\).
Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là
5 mặt, 10 cạnh.
6 mặt, 5 cạnh.
6 mặt, 10 cạnh.
5 mặt, 5 cạnh.
Chọn mệnh đề đúng trong các mệnh đề sau:
Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
Hai đường thẳng phân biệt không có điểm chung thì chéo nhau.
Hai đường thẳng chéo nhau thì không có điểm chung.
Hai đường thẳng không có điểm chung thì chéo nhau.
Tập xác định của hàm số \[y = \tan x\] là
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\].
\[D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\].
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\].
\[D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\].
Số đo độ của góc \(\frac{\pi }{6}\) là
\({30^0}\)
\({45^0}\)
\({90^0}\)
\({60^0}\)
Điều khẳng định nào sau đây là đúng?
\[\tan \alpha = \tan \left( {{{180}^0} - \alpha } \right)\].
\[\cot \alpha = \cot \left( {{{180}^0} - \alpha } \right)\].
\(\cos \alpha = \cos \left( {{{180}^0} - \alpha } \right)\).
\(\sin \alpha = \sin \left( {{{180}^0} - \alpha } \right)\).
Cho cấp số cộng \(({u_n})\)có \({u_6} = - 32;\;{u_7} = 64\). Công sai của cấp số đó là
\(d = 32\).
\(d = - 2\).
\(d = 96\).
\(d = - 32\).
Thiết diện của một mặt phẳng với một tứ diện chỉ có thể là:
Một tam giác hoặc một ngũ giác.
Một tứ giác hoặc một ngũ giác.
Một tam giác và một hình bình hành.
Một tam giác hoặc một tứ giác.
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\)là hình thang, \(AD{\rm{//}}BC\), \(AD = 2BC\). \(M\)là trung điểm của \(SA\). Mặt phẳng \(\left( {MBC} \right)\)cắt hình chóp theo thiết diện là
Hình bình hành.
Tam giá
Hình chữ nhật.
Hình thang.
Có hai cơ sở khoan giếng A và Cơ sở A giá mét khoan đầu tiên là \(8000\)(đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm \(500\)(đồng) so với giá của mét khoan ngay trước đó. Cơ sở B. Giá của mét khoan đầu tiên là \(6000\)(đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm \(7\% \)giá của mét khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần lượt là \(20\)\[\left( {\rm{m}} \right)\]và \(25\)\[\left( {\rm{m}} \right)\]để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất?
giếng \(20\)\[\left( {\rm{m}} \right)\]chọn A còn giếng \(25\)\[\left( {\rm{m}} \right)\]chọn B
luôn chọn B
giếng \(20\)\[\left( {\rm{m}} \right)\]chọn B còn giếng \(25\)\[\left( {\rm{m}} \right)\]chọn B
luôn chọn A
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho lăng trụ tam giác \(ABC \cdot A'B'C'\). Gọi \(I\) và \(I'\) lần lượt là trung điểm của \(BC\) và \(B'C'\).
a) \(AA'I'I\)là hình bình hành.
b) \(II'\parallel BB'\).
c) Giao tuyến của \((AB'C')\) và \((A'BC')\) là đường thẳng đi qua giao điểm của hai đường thẳng \(AI'\), \(A'I\).
d) \(IA'\)song song \((AB'C')\).
Cho phương trình \(\left( {2\sin x - 1} \right)\left( {\cos x + 1} \right) = 0\). Xét tính đúng sai của các khẳng định sau.
a) \(x = \frac{\pi }{6}\)là một nghiệm của phương trình.
b) Nghiệm âm lớn nhất của phương trình là \(x = \frac{{ - 7\pi }}{6}\).
c) Phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + k2\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \pi + k2\pi }\end{array}} \right.\).
d) Tổng các nghiệm của phương trình thuộc nửa khoảng \(\left[ { - 2\pi ;3\pi } \right)\) bằng \(3\pi \).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Một cây cầu có dạng hình cung \(OA\) của đồ thị hàm số \(y = \frac{{48}}{{10}}\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ \(Oxy\) với đơn vị trên trục là mét như hình vẽ. Độ rộng giữa hai chân cầu là chiều dài đoạn \(OA\) bằng bao nhiêu mét? (làm tròn kết quả đến hàng phần mười)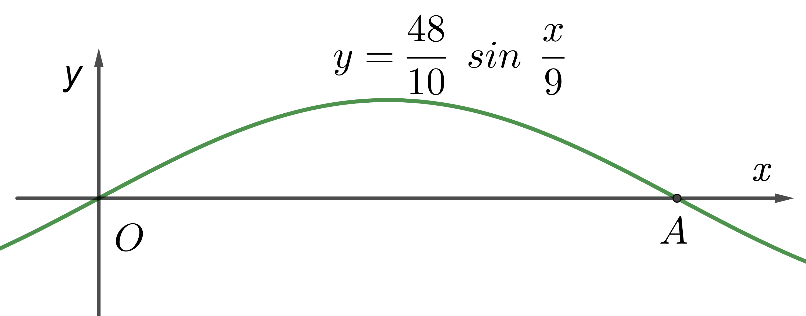
Theo báo cáo của Chính phủ, dân số của nước ta tính đến tháng 12 năm 2020 là 97,58 triệu người, nếu tỉ lệ tăng trưởng dân số trung bình hằng năm là \(1,14\% \) thì dân số nước ta vào tháng 12 năm 2025 là bao nhiêu? (Tính theo đơn vị triệu người, làm tròn đến hàng đơn vị)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Cho phương trình \(1 + 6 + 11 + 16 + \cdots + x = 970\). Biết rằng \(1,6,11, \cdots x\) là một cấp số cộng, Tìm \(x\)?
Cho hình chóp \[S.ABCD\], đáy \[ABCD\] là hình thang, đáy lớn \[AB\]. Gọi \[N,P\] lần lượt là trung điểm của \[SA,SB\]. \[M\] là một điểm tùy ý thuộc đoạn \[SD\] (\[M\] không trùng với \[D\]). Tìm giao điểm của \[SC\] với \[(MNP)\]
Một cây cầu có dạng cung \(OA\) là một phần của đồ thị hàm số \(y = 4,8\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như hình bên.
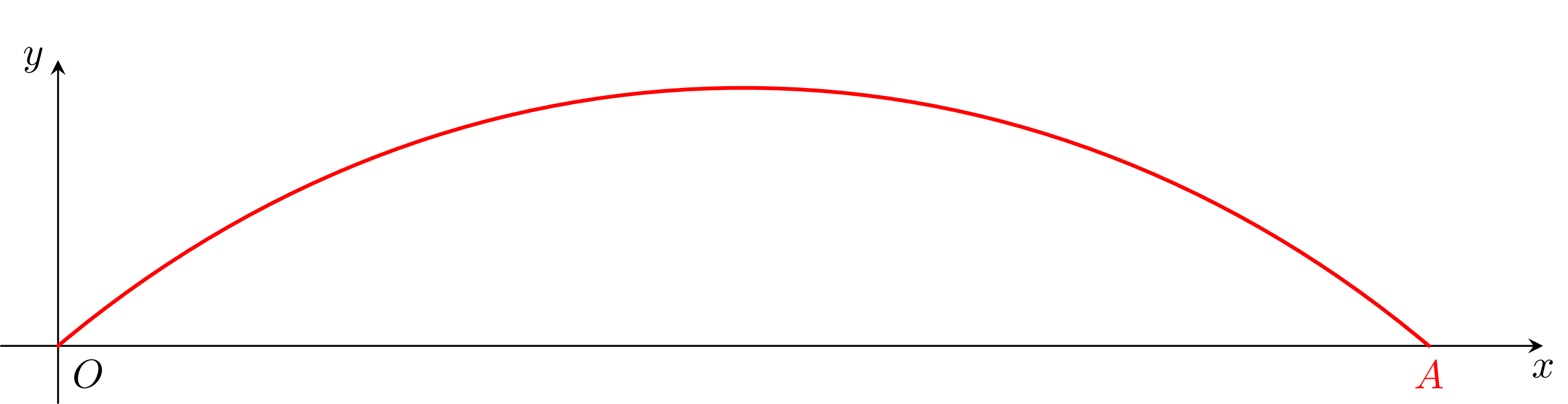
Giả sử chiều rộng của con sông là độ dài đoạn thẳng \(OA\). Chiều rộng đó (làm tròn đến kết quả hàng phần mười) là








