Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 12
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD.\) Cặp đường thẳng nào sau đây cắt nhau?
\(BG\)và\(CD\).
\(AG\)và\(BC\).
\(AB\)và\(CD\).
\(AC\)và\(BD\).
Cho dãy số \(\left( {{u_n}} \right)\), với \({u_{n - 1}} = {2^n} + 1\). Giá trị \({u_5}\) bằng
\(127\).
\(15\).
\(33\).
\(65\).
Cho góc lượng giác \[\alpha \]. Tìm mệnh đề sai (giả thiết các vế đều có nghĩa).
\[\tan \left( {\pi + \alpha } \right) = \tan \alpha \].
\[\sin \left( {\pi + \alpha } \right) = \sin \alpha \].
\[\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \].
\[\sin \left( { - \alpha } \right) = - \sin \alpha \].
Trong các công thức sau, công thức nào đúng?
\(\sin 2a = 2\sin a\cos a\).
\(\sin 2a = 2\sin a\).
\(\sin 2a = \sin a + \cos a\).
\(\sin 2a = {\cos ^2}a - {\sin ^2}a\).
Tìm tập xác định của hàm số \(y = \tan x\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k2\pi \,|k \in \mathbb{Z}} \right\}\).
Chọn khẳng định sai trong các khẳng định sau.
Nếu ba điểm phân biệt \(M,N,P\) cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Cấp số cộng \({u_n}\) có số hạng đầu là \({u_1}\)công sai là \(d\). Công thức số hạng tổng quát của \({u_n}\) là
\({u_n} = {u_1} - nd\).
\({u_n} = {u_1} + nd\).
\({u_n} = {u_1} + \left( {n + 1} \right)d\).
\({u_n} = {u_1} + \left( {n - 1} \right)d\).
Nghiệm của phương trình \(\sin x = - 1\) là
\(x = \frac{{ - \pi }}{2} + k2\pi \).
\(x = \frac{{ - \pi }}{2} + \frac{{k\pi }}{2}\).
\(x = \frac{{ - \pi }}{2} + k\pi \).
\(x = - \pi + k2\pi \).
Góc có số đo \[{108^{\rm{o}}}\]đổi ra radian là
\[\frac{\pi }{4}\].
\[\frac{{3\pi }}{5}\].
\[\frac{\pi }{{10}}\].
\[\frac{{3\pi }}{2}\].
Cho hình chóp tứ giác \(S.ABCD.\) Gọi \(O\) là giao điểm của \(AC\) và \(BD,\) điểm \(E\) thuộc cạnh \(SA.\) Thiết diện của hình chóp cắt bởi mặt phẳng\(\left( {DOE} \right)\) là hình gì?
Ngũ giác.
Hình bình hành.
Hình thang.
Tam giác.
Cho tứ diện \[ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[BC,BD\]. Giao tuyến của hai mặt phẳng \[\left( {AIJ} \right)\] và \[\left( {ACD} \right)\] là
Đường thẳng \[d\] đi qua \[A\] và \[d//BC\].
Đường thẳng \[d\] đi qua \[A\] và \[d//BD\].
Đường thẳng \[AB\].
Đường thẳng \[d\] đi qua \[A\] và \[d//CD\].
Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có diện tích \[{S_1}\]. Gọi \[{A_n},\,{B_n},\,{C_n},\,{D_n}\,\,\left( {n \in \mathbb{N},\,n \ge 2} \right)\] lần lượt là trung điểm của \[{A_{n - 1}}{B_{n - 1}},\,{B_{n - 1}}{C_{n - 1}},\,{C_{n - 1}}{D_{n - 1}},\,{D_{n - 1}}{A_{n - 1}}\]. Hình vuông \[{A_n}{B_n}{C_n}{D_n}\] có diện tích \[{S_n}\]. Tính giới hạn tổng diện tích \[n\] hình vuông đầu tiên.
\[2{S_1}\].
\[S_1^2\].
\[\frac{{{S_1}}}{2}\].
\[{S_1}\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = 2\sin \left( {\frac{{5\pi }}{2} - \frac{{\pi x}}{6}} \right) + 11\). Xét tính đúng sai của các khẳng định sau.
a) Hàm số tập xác định là \(\mathcal{D} = \mathbb{R}\).
b) Hàm số là hàm số chẵn.
c) Hàm số tuần hoàn với chu kì \(T = 12\pi \).
d) Giá trị lớn nhất của hàm số là \(13\).
Cho hình chóp \(S.ABCD\) có đáy là hình thoi tâm \(O\). Gọi \(M,N\) theo thứ tự là trung điểm của \(SA,BC\). Các mệnh đề sau đúng hay sai?
a) Giao tuyến của hai mặt phẳng \((MBD)\) và \((SAC)\) là đường thẳng \(OM\).
b) Giao tuyến của hai mặt phẳng \((DMN)\) và \((SAC)\) là đường thẳng \(ME\) với \(E\) là trung điểm của đoạn thẳng \(OC\).
c) Giao điểm giữa đường thẳng \(CM\) và mặt phẳng \((SBD)\) là trọng tâm tam giác \(SAC\).
d) Có đúng \(2\) mặt phẳng phân biệt chứa điểm \(O\) trong các mặt phẳng được tạo từ \(5\) điểm \(S,A,B,C,D\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là \(13,5\) triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm \(500.000\) đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận được sau ba năm làm việc cho công ty.
Một công viên giải trí vừa khánh thành trò chơi Vòng quay tốc độ. Giả sử tại thời điểm \(t\), buồng A trên vòng quay cách mặt đất một độ cao được cho bởi công thức \(p\left( t \right) = 20 + 10\sin \left( {\frac{{\pi \left( {t - 1} \right)}}{5}} \right)\). Biết rằng tại thời điểm \(t = 0\) thì vòng bắt đầu quay. Trong 10 giây đầu tiên, tại thời điểm giây bao nhiêu thì độ cao của buồng A đạt 30 mét?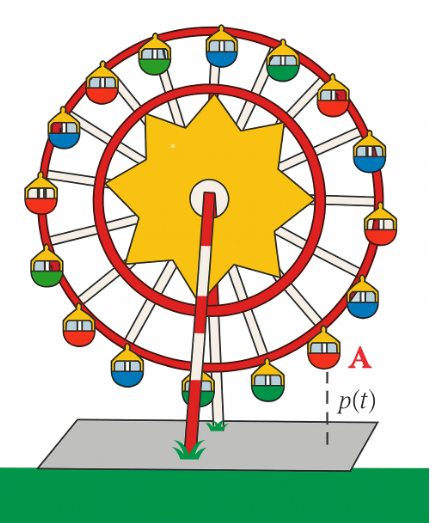
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Cho tứ diện \(SABC\). Trên đoạn \(SC\) lấy điểm \(M\) sao cho \(3SM = 2MC\). Gọi \(N\), \(K\) lần lượt là trung điểm của các cạnh \(BC\), \(SA\). Gọi \(I\) là giao điểm của đường thẳng \(AB\) và mặt phẳng \(\left( {KMN} \right)\). Biết \(AB = 2\sqrt 3 \). Độ dài cạnh \(IA\) bằng bao nhiêu? (Làm tròn kết quả đến hai chữ số thập phân)
Người ta trồng cây theo hình tam giác, với quy luật: ở hàng thứ nhất có \(1\) cây, ở hàng thứ hai có \(2\) cây, ở hàng thứ ba có \(3\) cây, …ở hàng thứ \(n\) có \(n\) cây. Biết rằng người ta trồng hết \(4950\) cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
Cho vận tốc \(v({\rm{cm/s}})\) của một con lắc đơn theo thời gian \(t\) (giây) được cho bởi công thức \(v = - 3\sin \left( {1,5t + \frac{\pi }{3}} \right)\). Xác định các thời điểm \(t\) mà tại đó








