Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 11
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Tập xác định của hàm số \[y = \tan x\] là
\[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\].
\[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\frac{\pi }{2},\,\,k \in \mathbb{Z}} \right\}\].
\[\mathbb{R}\backslash \left\{ {k\pi ,\,\,k \in \mathbb{Z}} \right\}\].
\[\mathbb{R}\].
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang ( đáy lớn là \(AB\)). Gọi \(M\), \(N\) lần lượt là trung đểm của \(SA\) và \(SB\).Chọn khẳng định sai:
\(MN\,{\rm{//}}\,{\rm{AD}}\).
\(MN\,{\rm{//}}\,CD\).
\(MN = \frac{1}{2}AB\).
\(MN\,{\rm{//}}\,{\rm{AB}}\).
Mệnh đề nào sau đây là sai?
\[\sin x = 0 \Leftrightarrow x = k{\rm{\pi }}\]
\[\sin x = - 1 \Leftrightarrow x = - \frac{{\rm{\pi }}}{2} + k2{\rm{\pi }}\]
\[\sin x = 0 \Leftrightarrow x = k2{\rm{\pi }}\].
\[\sin x = 1 \Leftrightarrow x = \frac{{\rm{\pi }}}{2} + k2{\rm{\pi }}\].
Trong các công thức sau, công thức nào sai?
\(\cos 2a = 2{\cos ^2}a - 1\).
\(\cos 2a = 1 - 2{\sin ^2}a\).
\(\cos 2a = {\cos ^2}a - {\sin ^2}a\).
\(\cos 2a = {\cos ^2}a + {\sin ^2}a\).
Với mọi \(\alpha \) thì \(\sin \left( {\frac{{3\pi }}{2} + \alpha } \right)\) bằng
\( - \sin \alpha \).
\(\sin \alpha \).
\( - \cos \alpha \).
\(\cos \alpha \).
Hình nào trong các hình sau là hình biểu diễn của hình chóp tứ giác?
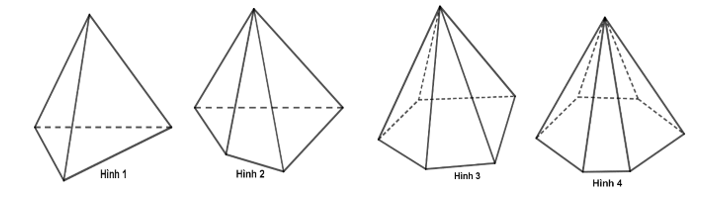
Hình \[3\].
Hình \[2\].
Hình \[1\].
Hình \[4\].
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 2\) và công sai \(d = 7\). Công thức của số hạng tổng quát là
\({u_n} = - 2 + 7.\left( {n - 1} \right)\).
\({u_n} = 7 - 2\left( {n - 1} \right)\).
\({u_n} = - 2 + 7n\).
\({u_n} = - {2.7^{n - 1}}\).
Đổi số đo góc \[\frac{{ - \pi }}{6}\] sang đơn vị độ:
\( - {30^0}\).
\({30^0}\).
\( - {330^0}\).
\( - {60^0}\).
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_1} = {u_2} = 1\)và \({u_{n + 2}} = {u_{n + 1}} + {u_n},\,\,\forall n \in \mathbb{N}*\). Tính \({u_4}\)
\(4\).
\(2\).
\(5\).
\(3\).
Cho hình chóp\[S.ABCD\], gọi \[M,N,P\] theo thứ tự là trung điểm của các cạnh \[BC,CD\] và\[SA\]. Mặt phẳng \[\left( {MNP} \right)\]cắt hình chóp \[S.ABCD\]theo thiết diện là hình gì?
Tam giác.
Lục giác.
Ngũ giác.
Tứ giác.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Giao tuyến của \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là
Đường \(SO\) với \(O\) là tâm hình bình hành.
Đường thẳng qua \(S\) và song song với \(CD\).
Đường thẳng qua \(S\) và song song với \(AD\).
Đường thẳng qua \(S\) và cắt \(AB\).
Chị Lan có \(400\)triệu đồng mang đi gửi tiết kiệm ở hai loại kì hạn khác nhau đều theo thể thức lãi kép. Chị gửi \(200\)triệu đồng theo kì hạn quý với lãi suất \(2,1\% \)một quý, \(200\)triệu đồng còn lại chị gửi theo kì hạn tháng với lãi suất \(0,73\% \)một tháng. Sau khi gửi được đúng \[1\]năm, chị rút ra một nửa số tiền ở loại kì hạn theo quý và gửi vào loại kì hạn theo tháng. Hỏi sau đúng \[2\]năm kể từ khi gửi tiền lần đầu, chị Lan thu được tất cả bao nhiêu tiền lãi (làm tròn đến hàng nghìn)?
\(79760000\).
\(65393000\).
\(70656000\).
\(74813000\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tứ diện \(ABCD\). Gọi \(M\) là điểm trên cạnh \(AB\) sao cho \(2AM = MB\) và \(G\) là trọng tâm của tam giác \(BCD\). Cho biết tính đúng, sai của mỗi phát biểu sau:
a) Gọi \((P)\) là mặt phẳng đi qua \(M\) và song song với mặt phẳng \((BCD)\). Thiết diện của tứ diện cắt bởi \((P)\) là một tam giác.
b) Hai đường thẳng \(AG\) và \(CD\) chéo nhau.
c) Nếu lấy điểm \(N\) trên cạnh \(AC\) sao cho \(2AN = NC\) thì đường thẳng \(MN\) song song với \(BD\).
d) Đường thẳng \(MG\) song song với mặt phẳng \((ACD)\).
Cho phương trình lượng giác \(\cot 3x = - \frac{1}{{\sqrt 3 }}\) (*). Khi đó
a) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};0} \right)\) bằng \(\frac{{ - 5\pi }}{9}\)
b) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{{2\pi }}{9}\)
c) Phương trình (*) có nghiệm \(x = \frac{\pi }{9} + k\frac{\pi }{3}(k \in \mathbb{Z})\)
d) Phương trình (*) tương đương \(\cot 3x = \cot \left( {\frac{{ - \pi }}{6}} \right)\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Giả sử một thành phố có dân số năm \(2022\) là khoảng \(2,1\) triệu người và trong những năm tiếp theo, cứ năm sau dân số lại tăng thêm \(0,75\% \) so với năm trước đó. Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì uớc tính vào năm nào dân số của thành phố đó sẽ khoảng \(2.262.923\) người?
Một chiếc cầu bắt qua sông, mặt dưới gầm cầu có dạng hình cung \[AB\] biểu thị bởi hàm số \(y = \frac{8}{{\sqrt 3 }}\cos \frac{x}{{12}} + 2\) với \(x \in \left[ { - 6\pi ;6\pi } \right]\) như hình minh họa sau

Biết qui định chiều cao tối đa của phương tiện giao thông hàng hóa qua lại dưới gầm cầu phải thấp hơn mặt nước gầm ít nhất 0,8 mét. Một sà lan chở khối hàng hóa có hình dạng là một khối hộp chữ nhật với độ cao 5,2 mét so với mặt nước sông muốn đi qua gầm cầu. Tính bề rộng tối đa của khối hàng hóa để sà lan qua được gầm cầu đúng qui định (lấy số \(\pi \approx 3,14\)) (làm tròn kết quả đến hàng phần mười)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
An và Bình chơi bài. Người thua phải trả 1 cây kẹo cho người thắng trong ván đầu tiên; 2 cây kẹo trong ván thứ 2; 4 cây kẹo trong ván thứ 3 và cứ thế số kẹo mỗi lần thua tăng gấp đôi so với lần trước đó. Ban đầu An có 625 cây kẹo và sau 10 ván thì An thua hết kẹo (có ván thắng, có ván thua). An nói với Bình: “Nếu chúng ta không chơi theo luật vừa rồi mà chơi theo luật khác: ván đầu người thua trả 10 cây cho người thắng, ván 2 trả 20 cây, ván 3 trả 30 cây thì tớ vẫn còn chơi với cậu được vài ván nữa”. Vậy, bạn An nói đúng hay sai?
Cho tứ diện đều \(ABCD\) có cạnh bằng \(2\). Gọi \(G\) là trọng tâm tam giác \(ABC\). Cắt tứ diện bởi mặt phẳng \((GCD)\). Tính diện tích của thiết diện. (làm tròn đến hàng phần mười)
Nhiệt độ cao bình thường hàng ngày \(T\) (tính theo độ Fahrenheit) tại Savannah, Georgia có thể được xấp xỉ bởi \(T = 76,4 + 16\cos \left( {\frac{{\pi t}}{6} - \frac{{7\pi }}{6}} \right)\) trong đó \(t\) là thời gian (tính theo tháng), với \(t = 1\) ứng với tháng Giêng. Gọi nhiệt độ cao bình thường hàng ngày cho các Tháng Giêng; Tháng Bảy; Tháng Mười lần lượt là \(a;b;c\). Tính \(a + b - c\)








