Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 10
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hai đường thẳng phân biệt \[a\] và \[b\] cùng thuộc mp\[(\alpha )\]. Có bao nhiêu vị trí tương đối giữa \[a\] và\[b\]?
1.
3.
4.
2.
Tìm tập xác định \(D\) của hàm số \(y = \tan \left( {x - \frac{\pi }{4}} \right)\).
\(D = \left\{ {\left. {x \in \mathbb{R}} \right|x \ne \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \left\{ {\left. {x \in \mathbb{R}} \right|x \ne \frac{{3\pi }}{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \left\{ {\left. {x \in \mathbb{R}} \right|x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \left\{ {\left. {x \in \mathbb{R}} \right|x \ne \frac{{3\pi }}{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Cho \(\sin \alpha = \frac{3}{4}\). Khi đó, \(\cos 2\alpha \)bằng
\[\frac{1}{8}\].
\[ - \frac{{\sqrt 7 }}{4}\].
\( - \frac{1}{8}\).
\[\frac{{\sqrt 7 }}{4}\].
Nghiệm phương trình \(2\sin x = 1\) có dạng nào dưới đây?
\(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + k2\pi }\\{x = - \frac{\pi }{6} + k2\pi }\end{array}} \right.\quad \left( {k \in \mathbb{Z}} \right)\).
\(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.\quad \left( {k \in \mathbb{Z}} \right)\).
\(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3} + k2\pi }\\{x = \frac{{2\pi }}{3} + k2\pi }\end{array}} \right.\quad \left( {k \in \mathbb{R}} \right)\).
\(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{6} + k2\pi }\\{x = - \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.\quad \left( {k \in \mathbb{R}} \right)\).
Cho dãy số \[\left( {{u_n}} \right)\], biết \({u_1} = - 1,\,\,{u_{n + 1}} = {u_n} + 3,\,\,\forall n \ge 1\). Ba số hạng đầu của dãy số đó là?
\(4;\,\,7;\,\,10\).
\( - 1;\,\,2;\,\,5\).
\(2;\,\,5;\,\,8\).
\(1;\,\,4;\,\,7\).
Cung có số đo 250o thì có số đo theo đơn vị rađian là
\(\frac{{35\pi }}{{18}}\).
\(\frac{{25\pi }}{9}\).
\(\frac{{25\pi }}{{18}}\).
\(\frac{{25\pi }}{{12}}\).
Trong các dãy số sau, dãy số nào là cấp số cộng?
\(1; - 3; - 5; - 7; - 9\).
\(1; - 3; - 6; - 9; - 12\).
\(1; - 2; - 4; - 6; - 8\).
\(1; - 3; - 7; - 11; - 15\).
Hình chóp ngũ giác có bao nhiêu cạnh?
\(11\).
\(10\).
\(5\).
\(8\).
Cho góc lượng giác \(a\) và \(k \in \mathbb{Z}\). Với điều kiện các biểu thức dưới đây có nghĩa, hỏi khẳng định nào sai?
\(\cos \left( {a + k4\pi } \right) = \cos a\).
\(\sin \left( {a + \left( {2k + 1} \right)\pi } \right) = - \sin a\).
\(\tan \left[ {a + \left( {2k - 1} \right)\pi } \right] = - \tan a\).
\(\cot \left( {a + k2\pi } \right) = \cot a\).
Cho bốn điểm \(A,\,B,\,C,\,D\) không cùng nằm trong một mặt phẳng. Trên các cạnh\(AB,\,AD\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \(MN\) cắt \(BD\) tại \(I\). Hỏi có bao nhiêu khẳng định đúng trong các khẳng định dưới đây?
\(\left( I \right)\): \(I\)là giao điểm của đường thẳng \(MN\)với mặt phẳng\[\left( {BCD} \right)\].
\(\left( {II} \right)\): \(I\)thuộc mặt phẳng \[\left( {ABC} \right)\].
\(\left( {III} \right)\): \(MN\)là giao tuyến của mặt phẳng \[\left( {MNC} \right)\]và mặt phẳng \[\left( {ABI} \right)\].
\(\left( {IV} \right)\): Thiết diện của hình chóp \(ABCD\)khi cắt bởi mặt phẳng \[\left( {MNC} \right)\] là tam giác \(MNC\).
\[2\].
\[4\].
\[1\].
\[3\].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Khi đó khẳng định nào sau đây là đúng? 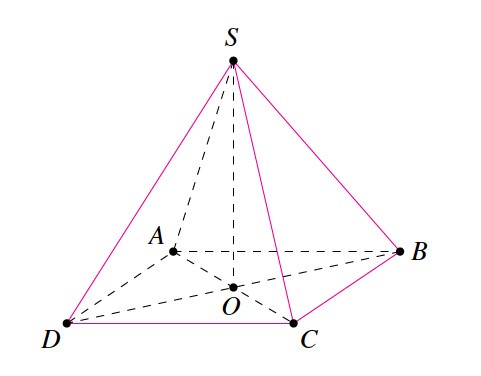
Đường thẳng \(d\) đi qua \(S\) và song song với \(AB\) và \(CD\).
Đường thẳng \(d\) nằm trong mặt phẳng \(ABCD\).
Đường thẳng \(d\) trùng với đường thẳng \(SO\).
Đường thẳng \(d\) đi qua \(S\) và song song với \(AD\) và \(BC\).
Trong dịp hội trại hè 2017, bạn Anh thả một quả bóng cao su từ độ cao \[6\left( {\rm{m}} \right)\] so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết rằng quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng:
\[44\,\left( {\rm{m}} \right)\].
\[42\,\left( {\rm{m}} \right)\].
\[43\,\left( {\rm{m}} \right)\].
\[45\,\left( {\rm{m}} \right)\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \sqrt 2 \cos \left( {2x + \frac{\pi }{4}} \right) + \sin \left( {2x - \frac{\pi }{2}} \right)\). Xét tính đúng sai của các khẳng định sau.
a) Rút gọn biểu thức ta được \(y = \sin 2x\).
b) Nếu \(\sqrt 2 \cos \left( {2x + \frac{\pi }{4}} \right) + \sin \left( {2x - \frac{\pi }{2}} \right) = - \frac{1}{3}\) thì giá trị biểu thức \(P = \frac{{2\tan 2x + \cot 2x}}{{4\tan 2x - 3\cot 2x}}\) là \(\frac{5}{{14}}\).
c) Hàm số tuần hoàn với chu kì \(\frac{\pi }{2}\).
d) Tập xác định của hàm số là \(\mathbb{R}\).
Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AD\) là đáy lớn và \(AD = 2BC\). Gọi \(E\) là giao điểm của \(AB\) và \(CD\), \(F\) là trung điểm \(AD\).
a) Giao tuyến của \((SAC)\) và \((SAD)\) là đường thẳng \(SA\).
b) Giao tuyến của \((SAB)\) và \((SCD)\) là đường thẳng \(SE\).
c) Giao tuyến của \((SAB)\) và \((SFC)\) là đường thẳng \(d'\) đi qua \(S\) và song song cạnh \(CD\).
d) Giao tuyến của \((SAD)\) và \((SBC)\) là đường thẳng \(d\) đi qua \(S\) và song song cạnh \(CD\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
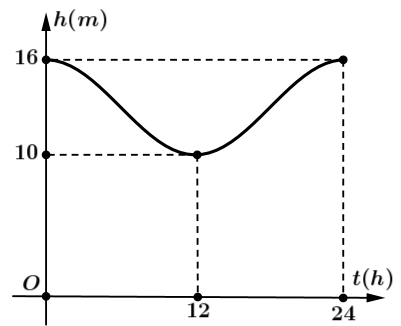
Mực nước cao nhất tại một cảng biển là \(16{\rm{\;m}}\) khi thủy triều lên cao và sau 12 giờ khi thủy triều xuống thấp thì mực nước thấp nhất là \(10{\rm{\;m}}\). Đồ thị ở hình dưới đây mô tả sự thay đổi chiều cao của mực nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước \(h\left( {{\rm{\;m}}} \right)\) theo thời gian \(t\left( {{\rm{\;h}}} \right)\left( {0 \le t \le 24} \right)\) được cho bởi công thức \(h = m + a{\rm{cos}}\left( {\frac{\pi }{{12}}t} \right)\) với \(m,a\) là các số thực dương cho trước. Tìm thời điềm trong ngày khi chiều cao của mực nước là \(11,5{\rm{\;m}}\) và tính tổng các thời điểm đó.
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài \(150{\rm{\;m}}\). Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng \(60\% \) so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình vẽ).
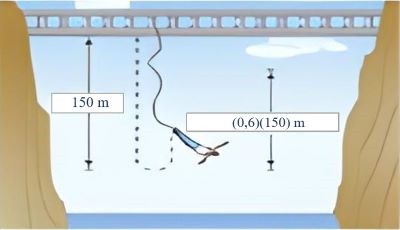
Tính tổng quãng đường bằng bao nhiêu mét khi mà người đó đi được sau 15 lần kéo lên và lại rơi xuống (làm tròn kết quả đến hàng đơn vị)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Cho tứ diện ABCD. Trên AC,AD lần lượt lấy các điểm M,N sao cho MN không song song với CD. Gọi O là điểm thuộc miền trong tam giác BCD. Tìm giao điểm của đường thẳng BD và mặt phẳng (OMN).
Một nhà thi đấu có \(10\) hàng ghế dành cho khán giả. Hàng thứ nhất có \(34\) ghế, hàng thứ hai có \(37\) ghế, hàng thứ ba có \(40\) ghế,.Cứ như thế, số ghế ở hàng sau nhiều hơn số ghế ở hàng ngay trước là 3 ghế. Trong một giải thi đấu, ban tổ chức đã bán được hết số vé phát ra và số tiền thu được từ bán vé là \(34200000\) đồng. Tính giá tiền của mỗi vé (đơn vị: nghìn đồng), biết số vé bán ra bằng sốghế dành cho khán giả cùa nhà thi đấu và các vé là đồng giá?
Có bao nhiêu giá trị nguyên của \(m \in [0;2024]\) để hàm số \(y = \sin \left( {\frac{{2x}}{{{x^2} + 2x + {m^2} + 3}}} \right)\) có tập xác định là \(\mathcal{D} = \mathbb{R}\)?








