Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 1
19 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho dãy số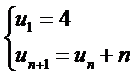 
. Năm số hạng đầu của dãy số là
\[4,\,16,\,32,\,64,\,128.\]
\[4,\,6,\,9,\,13,\,18.\]
\[4,\,5,\,7,\,10,\,14.\]
\[4,\,5,\,6,\,7,\,8.\]
Trong các công thức sau, công thức nào sai?
\[\cot 2x = \frac{{{{\cot }^2}x - 1}}{{2\cot x}}\].
\[\cos 3x = 4{\cos ^3}x - 3\cos x\].
\[\tan 2x = \frac{{2\tan x}}{{1 + {{\tan }^2}x}}\].
\[\sin 3x = 3\sin x - 4{\sin ^3}x\].
Trong các mệnh đề sau, mệnh đề nào đúng?
Hai đường thẳng phân biệt không song song thì cheo nhau.
Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
Hai đường thẳng chéo nhau thì không có điểm chung.
Hai đường thẳng không có điểm chung thì chéo nhau.
Cho cấp số cộng \(\left( {{u_n}} \right)\)có số hạng đầu \({u_1}\)và công sai \(d\). Công thức tìm số hạng tổng quát \({u_n}\)là:
\({u_n} = n{u_1} + d\).
\({u_n} = {u_1} + nd\).
\({u_n} = {u_1} + \left( {n - 1} \right)d\).
\({u_n} = {u_1} + \left( {n + 1} \right)d\).
Trong tam giác \[ABC\], đẳng thức nào dưới đây luôn đúng?
\[{\rm{cos}}\,A = \sin \,B\].
\[{\rm{cos}}\frac{{A + B}}{2} = \sin \frac{C}{2}\].
\(\tan \,A = \cot \left( {B + \frac{\pi }{2}} \right)\).
\(\sin \left( {A + B} \right) = {\rm{cos }}C\).
Cho tứ diện \(ABCD\). Gọi \(M\,,\,\,N\) lần lượt là trung điểm của \(AB\,,\,CD\) và điểm \(P\) thuộc cạnh \(BC\) sao cho \(P\) không là trung điểm của \(BC\). Cặp đường thẳng nào sau đây không cắt nhau?
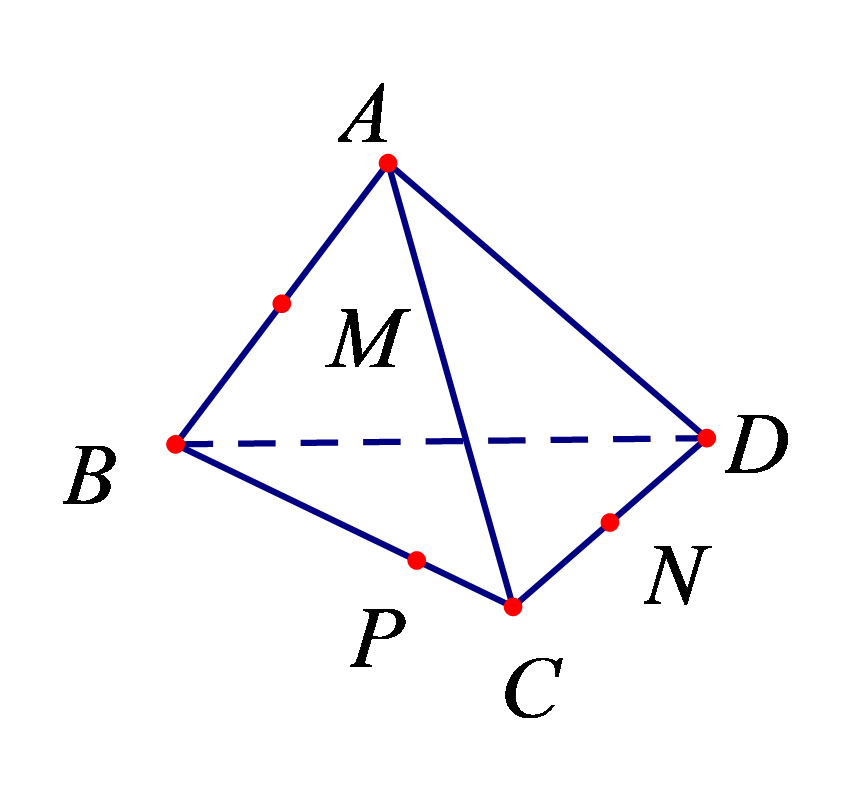
\(MN\) và \(BD\).
\(MP\) và \(AC\).
\(PN\) và \(BD\).
\(AP\) và \(CM\).
Tập xác định của hàm số \[y = \tan x\] là
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\[D = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},k \in \mathbb{Z}} \right\}.\]
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}.\)
Góc có số đo \(120^\circ \) đổi sang rađian là:
\(\frac{{3\pi }}{2}\).
\(\frac{\pi }{4}\).
\(\frac{\pi }{{10}}\).
\(\frac{{2\pi }}{3}\).
Phương trình nào sau đây vô nghiệm?
\[\sin x + 3 = 0\].
\[\tan x + 3 = 0\].
\[3\sin x - 2 = 0\].
\(2{\cos ^2}x - \cos x - 1 = 0\).
Cho hình chóp tứ giác\[S.ABCD\], đáy \[ABCD\] là hình bình hành, gọi \[M,N,Q\] lần lượt là trung điểm các cạnh\[AB,AD,SC\]. Thiết diện của hình chóp với mặt phẳng \[\left( {MNQ} \right)\] là đa giác có bao nhiêu cạnh?
\(4\).
\(3\).
\(6\).
\(5\).
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình thang \(\left( {AB\,{\rm{//}}\,CD} \right)\). Gọi \[I\], \[J\] lần lượt là trung điểm của \(AD\) và \(BC\), \(G\) là trọng tâm \(\Delta SAB\). Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\)và \(\left( {IJG} \right)\)là
\[SC\].
đường thẳng qua \(G\) và cắt \(BC\).
đường thẳng qua \(S\) và song song với \(AB\).
đường thẳng qua \(G\) và song song với \(DC\).
Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho dân với theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm \[10\]số; bậc \[1\]từ số thứ \[1\]đến số thứ \[10\], bậc \[2\]từ số thứ \[11\]đến số \[20\], bậc \[3\]từ số thứ \[21\]đến số thứ \[30\],…. Bậc \[1\]có giá là \[800\]đồng/\[1\] số, giá của mỗi số ở bậc thứ \[n + 1\]tăng so với giá của mỗi số ở bậc thứ \[n\]là \[2,5\% \]. Gia đình ông A sử dụng hết \[347\]số trong tháng \[1\], hỏi tháng \[1\]ông A phải đóngbao nhiêu tiền ? (đơn vị là đồng, kết quả được làm tròn đến hàng phần trăm).
\(x \approx 433868,89\).
\(x \approx 402832,28\).
\(x \approx 402903,08\).
\(x \approx 415481,84\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình lượng giác \(3 - \sqrt 3 \tan \left( {2x - \frac{\pi }{3}} \right) = 0\). Xét tính đúng sai của các khẳng định sau.
a) Khi \( - \frac{\pi }{4} < x < \frac{{2\pi }}{3}\) thì phương trình có \(3\) nghiệm.
b) Phương trình có nghiệm \(x = \frac{\pi }{6} + k\frac{\pi }{2}\), \(k \in \mathbb{Z}\).
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{6}\).
d) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{4};\frac{{2\pi }}{3}} \right)\) bằng \(\frac{\pi }{6}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\), \(N\), \(K\) lần lượt là trung điểm các cạnh \(AB\), \(BC\), \(SB\).
a) \((MNK)\parallel (SAD)\). b) \(NK\parallel (SCD)\).
c) \(MK\parallel (SAB)\). d) \((MNK)\parallel (SAC)\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu \(h(m)\)của mực nước trong kênh tính theo thời gian \(t(h)\) được cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 12\).\(\left( {0\, \le \,t\, \le \,24} \right)\). Xác định thời điểm trong ngày khi chiều cao của mực nước trong kênh là \(15\,\,m\).
Bạn Vân là học sinh giỏi của một trường THPT nên được hưởng học bổng hằng tháng là 4 triệu đồng. Học bổng được cấp vào đầu tháng. Vì muốn để dành tiền đóng học phí vào năm nhất đại học nên bắt đầu từ đầu tháng 9/2023 (đầu năm học lớp 11), cứ đầu tháng bạn Vân dành 30% số tiền học bổng nói trên để gửi tiết kiệm ở ngân hàng với lãi suất 0,4%/tháng và sẽ cố gắng giữ vững thành tích học tập để nhận học bổng đến hết tháng 8/2025. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu, học bổng được cấp đến hết tháng 8/2025. Hỏi đến hết tháng 8/2025 bạn Vân có bao nhiêu triệu đồng để đóng học phí học đại học (làm tròn kết quả đến hàng đơn vị)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Một cấp số cộng có \(7\) số hạng. Biết rằng tổng của số hạng đầu và số hạng cuối bằng \(30\), còn tổng của số hạng thứ ba và số hạng thứ sáu bằng \(35\). Tính số hạng thứ bảy của cấp số cộng đó.
Cho hình chóp S.ABC có hai điểm M,N lần lượt thuộc hai cạnh SA;SB và O là điểm nằm trong tam giác ABC. Xác định giao điểm của đường thẳng SO và mặt phẳng (CMN)
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để phương trình \(\cos \left( {2x - \frac{\pi }{3}} \right) - m = 2\) có nghiệm. Tính tổng các phần tử trong \(S\).
