Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 5)
20 câu hỏi
Mẫu thức của phân thức \(\frac{{{x^2}\left( {x + 1} \right)}}{{\left( {x - y} \right){y^2}}}\) là
\({x^2}\left( {x + 1} \right)\).
\(\left( {x - y} \right)\).
\(\left( {x - y} \right){y^2}\).
\({y^2}\).
Điều kiện xác định của phân thức \(\frac{{{x^2} - 1}}{{{x^2} - 2x + 1}}\) là
\(x = 1\).
\(x = 1;x = - 1\).
\(x \ne 1;x \ne - 1\).
\(x \ne 1\).
Giả sử các biểu thức đều có nghĩa. Áp dụng quy tắc đổi dấu ta viết được phân thức \(\frac{{5 - x}}{{11 - {x^2}y}}\) bằng phân thức
\(\frac{{5 - x}}{{11 + {x^2}y}}\).
\(\frac{{x - 5}}{{ - 11 + {x^2}y}}\).
\(\frac{{x + 5}}{{11 - {x^2}y}}\).
\(\frac{{x + 5}}{{11 + {x^2}y}}\).
Kết quả của biểu thức \(\frac{3}{{2x + 6}} - \frac{{x - 6}}{{2{x^2} + 6x}}\) là
\(\frac{1}{{x + 3}}.\)
\( - \frac{1}{{x + 3}}\).
\( - \frac{1}{x}.\)
\(\frac{1}{x}\).
Công thức nào dưới đây thể hiện phép nhân hai phân thức \(\frac{A}{B}\) với phân thức \(\frac{M}{N}\)?
\(\frac{A}{B}.\frac{M}{N} = \frac{{A + M}}{{B.N}}\).
\(\frac{A}{B}.\frac{M}{N} = \frac{{A.N}}{{B.M}}\).
\(\frac{A}{B}.\frac{M}{N} = \frac{{A.M}}{{B.N}}\).
\(\frac{A}{B}.\frac{M}{N} = \frac{{A.M}}{{B + N}}\).
Kết quả của phép tính \(\frac{{\left( { - 20x} \right)}}{{3{y^2}}}:\frac{{\left( { - 4{x^3}} \right)}}{{5y}}\) là
\(\frac{{80{x^3}}}{{15{y^3}}}\).
\(\frac{{25x}}{{3y}}\).
\(\frac{{25xy}}{{3{x^2}y}}\).
\(\frac{{25}}{{3{x^2}y}}\).
Đưa phương trình \(5x - \left( {6 - x} \right) = 12\) về dạng \(ax + b = 0\) ta được
\(4x + 6 = 0.\)
\(4x - 18 = 0\).
\(5x - 6 = 0\).
\(6x - 18 = 0\).
Giá trị \(x = - 4\) là nghiệm của phương trình nào dưới đây?
\( - \frac{5}{2}x + 1 = 11\).
\( - \frac{5}{2}x = - 10\).
\(3x - 8 = 0\).
\(3x - 1 = x + 7\).
Cho theo tỉ số \(k\). Vậy \(k\) bằng tỉ số nào dưới đây?
\(k = \frac{{AB}}{{BC}}\).
\(k = \frac{{AC}}{{DF}}\).
\(k = \frac{{DE}}{{AB}}.\)
\(k = \frac{{DE}}{{DF}}\).
Cho \(\Delta DEF\) vuông tại \(E\). Áp dụng định lí Pythagore vào tam giác trên ta được:
\(D{E^2} + E{F^2} = D{F^2}\).
\(D{F^2} + F{E^2} = D{E^2}\).
\(D{E^2} + D{F^2} = E{F^2}\).
\(E{F^2} - D{E^2} = D{F^2}\).
Cho \(\Delta ABC\) và \(\Delta DMN\) như hình vẽ dưới đây:
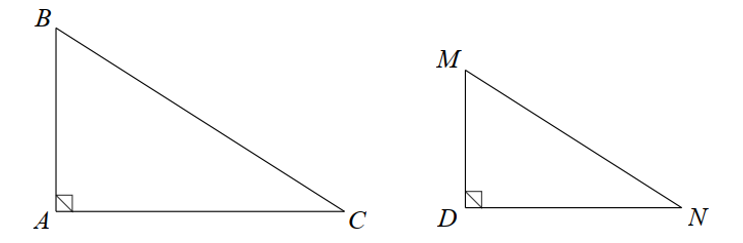
Để (cạnh huyền – cạnh góc vuông) thì cần thêm yếu tố nào dưới đây?
\(\frac{{AB}}{{DM}} = \frac{{AC}}{{DN}}\).
\(\frac{{BC}}{{AC}} = \frac{{MN}}{{DN}}\).
\(\widehat B = \widehat M\).
Cả ba đáp án trên đều đúng.
Trong các cặp hình sau, hình nào là hình đồng dạng?
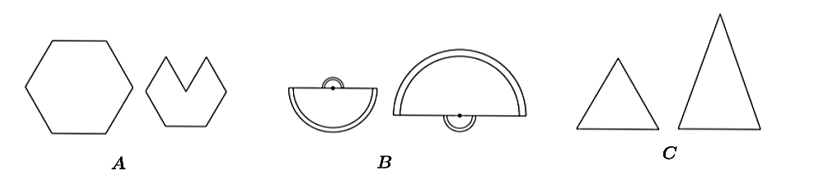
Hình \(A\).
Hình \(B.\)
Hình \(C\).
Không có hình nào.
Một miếng đất hình chữ nhật có chiều dài hơn chiều rộng \(25{\rm{ m}}\). Nếu giảm chiều dài đi \(25{\rm{ m}}\) thì diện tích sẽ nhỏ hơn diện tích ban đầu là \(1{\rm{ }}000{\rm{ }}{{\rm{m}}^2}\). Gọi chiều dài ban đầu của miếng dất là \(x\) \(\left( {x > 25,{\rm{ m}}} \right).\)
a) Chiều rộng ban đầu của miếng đất là \(x - 25{\rm{ }}\left( {\rm{m}} \right)\).
b) Khi chiều dài giảm đi \(25{\rm{ m}}\)ta được chiều dài mới bằng chiều rộng ban đầu của mảnh đất.
c) Phương trình mô tả bài toán là \(x\left( {x - 25} \right) - \left( {x - 25} \right)\left( {x - 25} \right) = 1{\rm{ }}000\).
d) Diện tích ban đầu của mảnh đất là \({\rm{2 600 }}\left( {{{\rm{m}}^2}} \right)\).
Cho \(\Delta BAC\) nhọn \(\left( {AB < AC} \right)\), đường cao \(AH\). Gọi \(D,E\) lần lượt là hình chiếu của \(H\) trên \(AB,AC\). Biết \(AH = 5{\rm{ cm,}}\)\(DE = 4{\rm{ cm,}}\)\(BC = 8{\rm{ cm}}\).
a)
b) \(A{H^2} = AD.AB\).
c)
d) \({S_{ADE}} = 5{\rm{ c}}{{\rm{m}}^2}\).
Cho biểu thức \(A = \frac{{x - 2}}{{x + 2}} - \frac{x}{{x - 2}} - \frac{{9x - 2}}{{4 - {x^2}}}\) \(\left( {x \ne 2;x \ne - 2} \right)\). Biết rằng, khi rút gọn \(A\), ta được \(A = \frac{a}{{x - 2}}\). Tìm giá trị của \(a\).
Cho biểu thức \(B = \left( {\frac{{7 - 2x}}{{x - 1}} + \frac{{2x}}{{x + 1}} - \frac{1}{{{x^2} - 1}}} \right):\frac{{3x + 9}}{{{x^2} - 1}}\) với \(x \ne 1;x \ne - 1\). Tính giá trị của \(B\) biết \(\left| {x - 2} \right| = 1\).
Tính tổng tất cả các giá trị của \(m\) để phương trình \(\left( {{m^2} - 4} \right)x = m - 2\) vô nghiệm.
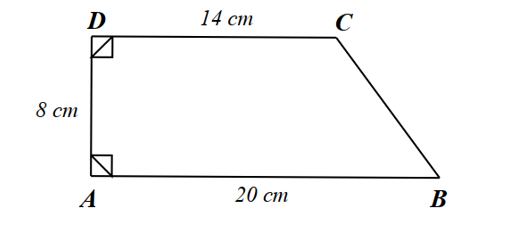
Cho hình vẽ bên. Chu vi của tứ giác \(ABCD\) là
Hai đội trồng cây rừng trong tháng trước được \(700\) cây. Trong tháng này đội I vượt mức \(60\% \) và đội II vượt mức \(40\% \). Tính xem mỗi đội trong tháng trước trồng được bao nhiêu cây. Biết rằng tháng này cả hai đội trồng được \(1{\rm{ }}100\) cây.
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 6{\rm{ cm,}}\)\(AC = 8{\rm{ cm}}\). Kẻ đường cao \(AH\). Gọi \(M,N\) lần lượt là hình chiếu của \(H\) trên \(AB,AC\).
a) Tính độ dài cạnh \(BC\).
b) Chứng minh \(AH.BC = AB.AC\) và .
c) Tính diện tích tứ giác \(BMNC\).








