Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 4)
20 câu hỏi
Điều kiện xác định của phân thức \(\frac{{x - 1}}{{{x^2} - 25}}\) là
\(x \ne 5\).
\(x \ne 25\).
\(x \ne - 5\).
\(x \ne 5;x \ne - 5\).
Chọn khẳng định đúng trong các khẳng định sau:
Đổi dấu tử của một phân thức, ta được phân thức mới bằng phân thức đã cho.
Đổi dấu mẫu của một phân thức, ta được phân thức mới bằng phân thức đã cho.
Đổi dấu cả tử và mẫu của phân thức, ta được phân thức mới bằng phân thức đã cho.
Cả ba ý trên đều đúng.
Trong các phép tính sau, đâu là phép cộng hai phân thức cùng mẫu?
\(\frac{1}{{x + y}} + \frac{{ - 3}}{x}\).
\(\frac{1}{{x + y}} + \frac{{ - 3}}{y}\).
\(\frac{1}{{x + y}} + \frac{{ - 3}}{{x + y}}\).
\(\frac{1}{{x + y}} + \frac{{x + y}}{3}\).
Kết quả của phép tính \(\frac{{11x}}{{2x - 3}} - \frac{{x - 18}}{{3 - 2x}}\) là
\(\frac{{18 - 10x}}{{2x - 3}}\).
\(\frac{{10x + 18}}{{2x - 3}}\).
\(\frac{{12x - 18}}{{2x - 3}}\).
\(\frac{{12x + 18}}{{2x - 3}}\).
Nghịch đảo của phân thức \(\frac{x}{{x + y}}\) là
\( - \frac{x}{{x + y}}\).
\( - \frac{{x + y}}{x}\).
\(\frac{{x + y}}{x}\).
\( - \frac{{y - x}}{x}\).
Kết quả của phép chia \(\frac{{8{y^2}}}{{9{x^2}}}:\frac{{4y}}{{3{x^2}}}\) là
\(\frac{{32{y^3}}}{{27{x^2}}}\).
\(\frac{{8y}}{3}\).
\(\frac{{2{y^2}}}{3}\).
\(\frac{{2y}}{3}\).
Phương trình nào dưới đây không phải phương trình bậc nhất một ẩn?
\(\frac{x}{5} + \frac{5}{3} = 0\).
\(1 + 2y = 0\).
\( - 3x + \frac{1}{2} = 0\).
\(2x - {x^2} = 0\).
Đưa phương trình \(2\left( {x + 2} \right) = 1 - 2x\) về dạng \(ax + b = 0\) là
\(4x + 3 = 0\).
\( - 2x + 1 = 0\).
\(4x + 5 = 0\).
\(2x + 4 = 0\).
\(\Delta ABC\) và \(\Delta DEF\) có \(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\). Cần thêm yếu tố nào để hai tam giác này đồng dạng?
\(\widehat A = \widehat D\).
\(\widehat B = \widehat E\).
\(\widehat C = \widehat F\).
Cả A, B, C đều sai.
Áp dụng định lí Pythagore cho tam giác vuông dưới đây ta được:
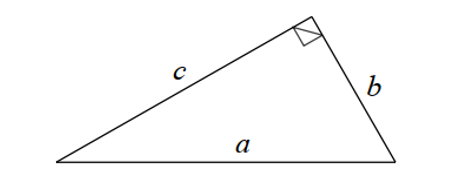
\({a^2} = {b^2} + {c^2}\).
\({b^2} = {a^2} + {c^2}\).
\({c^2} = {a^2} + {b^2}\).
\({a^2} = {\left( {b + c} \right)^2}\).
Cho hình vẽ dưới đây.
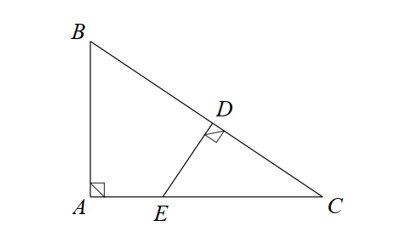
Hỏi đồng dạng theo trường hợp nào?
Góc – góc.
Cạnh – góc – cạnh.
Cạnh – cạnh – cạnh.
Góc – cạnh.
Chọn khẳng định đúng trong các khẳng định sau:
Tam giác bằng nhau thì đồng dạng.
Tam giác đồng dạng thì bằng nhau.
Tam giác bằng nhau thì không đồng dạng.
Tam giác vuông luôn đồng dạng với nhau.
Một xe khách đi từ \(A\) đến \(B\) với vận tốc \(20{\rm{ km/h}}\). Sau \(3\) giờ thì tại A có một xe con đuổi theo với vận tốc \(50{\rm{ km/h}}\). Gọi \(x\) (giờ) là thời gian từ lúc xe con đi tới đuổi kịp xe khách (\(x > 0\)).
a) Thời gian xe khách đi tới lúc gặp xe con là \(x + 3\) (giờ).
b) Quãng đường đi được của xe con là \(50\left( {x + 3} \right)\) (km).
c) Phương trình mô tả bài toán trên là \(20x = 50\left( {x + 3} \right)\).
d) Vậy sau \(3\) giờ thì xe con đuổi kịp xe khách.
Cho tam giác \(ABC\) vuông cân tại \(A\). Lấy \(D\) thuộc cạnh \(AC\), kẻ \(DM \bot BC{\rm{ }}\left( {M \in BC} \right)\). Tia \(MD\) cắt \(BA\) tại \(N\).
a) .
b) \(\frac{{BA}}{{BM}} = \frac{{BC}}{{BN}}\).
c) .
d) \({S_{BAM}} = 2{S_{BCN}}\).
Cho biểu thức \(P = \frac{{{x^2} - 6x + 9}}{{9 - {x^2}}} + \frac{{4x + 8}}{{x + 3}}\) với \(x \ne 3;x \ne - 3\). Biết rằng khi rút gọn \(P\) ta được \(P = \frac{{3x + a}}{{x + 3}}\). Tìm giá trị \(a\) thỏa mãn.
Cho biểu thức \(A = \left( {\frac{{a + 2}}{{a + 1}} - \frac{{a - 2}}{{a - 1}}} \right).\frac{{a + 1}}{a}\) và \(B = \frac{3}{{{a^2} - 1}}\) với \(a \ne 0;a \ne 1;a \ne - 1\). Tìm giá trị của \(a\) để \(A = 2B\).
Phương trình \(\frac{2}{3}\left( {x + m} \right) - x + \frac{1}{2} = 0\) nhận \(x = \frac{1}{3}\) là nghiệm thì giá trị của \(m\) là bao nhiêu?
Tính độ dài cạnh \(BC\) trong tam giác \(ABC\) cân tại \(A\) dưới đây.
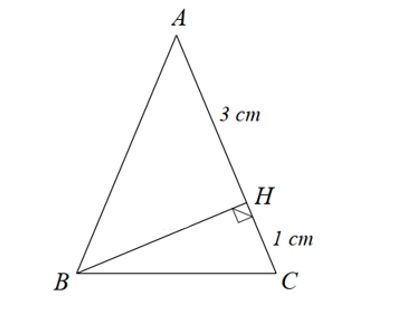
Một tổ dự định may mỗi ngày \(50\) cái áo. Nhưng thực tế mỗi ngày tổ đã may được \(60\) cái áo. Do đó không những tổ đã hoàn thành trước một ngày mà còn làm thêm được \(20\) cái áo nữa. Tính số lượng áo mà tổ phải may theo dự định ban đầu.
Cho \(\Delta ABC\) có \(AB = 4{\rm{ cm,}}\) \(BC = 5{\rm{ cm}}\). Cho \(AH\) là đường cao của \(\Delta ABC\).
a) Tính độ dài cạnh \(AC\).
b) Chứng minh và \(A{C^2} = CH.BC\).
c) Gọi \(M,N\) lần lượt là trung điểm của \(AH,BH\). Chứng minh rằng .








