Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
21 câu hỏi
Trong các biểu thức sau biểu thức nào là phân thức đại số?
\(\frac{{\sqrt x }}{{x - 3}}\).
\(\frac{{2x + 1}}{{x - 3}}\).
\(\frac{{\sqrt {2x} - 1}}{{x - 3}}\).
\(\frac{{2x + 1}}{{\sqrt {3x - 2} }}\).
Phân thức \(\frac{{2x + 1}}{{x - 3}}\) xác định khi:
\(x = 3.\)
\(x \ne 3.\)
\(x \ge 3.\)
\(x \le 3.\)
Phân thức \(\frac{{x + 1}}{{2x - y}}\) có phân thức đối là
\(\frac{{x - 1}}{{2x + y}}\).
\( - \frac{{x + 1}}{{2x - y}}\).
\(\frac{{x + 1}}{{2x + y}}\).
\(\frac{{2x - y}}{{x + 1}}\).
Giả sử các biểu thức đều có nghĩa, kết quả của phép tính \(\frac{a}{{a - 3}} - \frac{3}{{a + 3}}\) là
\(\frac{{{a^2} + 9}}{{{a^2} - 9}}\).
\(\frac{{{a^2} - 9}}{{{a^2} + 9}}\).
\(\frac{{{a^2} + 6}}{{{a^2} - 6}}\).
\(\frac{{{a^2} - 6}}{{{a^2} + 6}}\).
Phân thức \(\frac{{{x^2}y + 1}}{{3{x^2}y + 2x}}\) là phân thức nghịch đảo của
\( - \frac{{{x^2}y + 1}}{{3{x^2}y + 2x}}\).
\(\frac{{3{x^2}y + 2x}}{{{x^2}y + 1}}\).
\( - \frac{{3{x^2}y + 2x}}{{{x^2}y + 1}}\).
\(\frac{{{x^2}y - 1}}{{3{x^2}y - 2x}}\).
Giả sử các biểu thức đều có nghĩa, kết quả của phép tính \(\frac{{{x^2} - 25}}{{{x^2} - 3x}}:\frac{{{x^2} + 5x}}{{{x^2} - 9}}\) là
\(\frac{{x - 5}}{{{x^2}}}\).
\(\frac{{\left( {x - 3} \right)\left( {x - 5} \right)}}{{{x^2}}}\).
\(\frac{{\left( {x + 3} \right)\left( {x - 5} \right)}}{{{x^2}}}\).
\(\frac{{\left( {x - 3} \right)\left( {x + 5} \right)}}{{{x^2}}}\).
Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất một ẩn?
\(0x + 2 = 0\).
\(2x + 1 = 0\).
\( - 2x = 0.\)
\(\frac{x}{2} + 3 = 0\).
Phương trình \(\frac{{2x}}{3} + \frac{1}{2} = 0\) có hạng tử tự do là:
\(\frac{2}{3}\).
\(\frac{1}{3}.\)
\(2\).
\(\frac{1}{2}\).
Cho tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\). Chọn khẳng định đúng trong các khẳng định dưới đây:
\(\widehat B = \widehat {B'}\).
\(\widehat A = \widehat {B'}\).
\(\widehat A = \widehat {C'}\).
\(\widehat B = \widehat C\).
Cho tam giác \(MNP\) vuông tại \(P\) khi đó
\(M{N^2} = M{P^2} - N{P^2}\).
\(M{N^2} = N{P^2} + M{P^2}\).
\(N{P^2} = M{N^2} + M{P^2}\).
\(M{P^2} = M{N^2} + N{P^2}\).
Cho các mệnh đề sau:
(I). Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
(II). Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
Khẳng định nào dưới đây là đúng?
Chỉ có (I) đúng.
Chỉ có (II) đúng.
Cả (I) và (II) đúng.
Cả (I) và (II) sai.
Trong các hình dưới đây, hình nào đồng dạng với nhau?
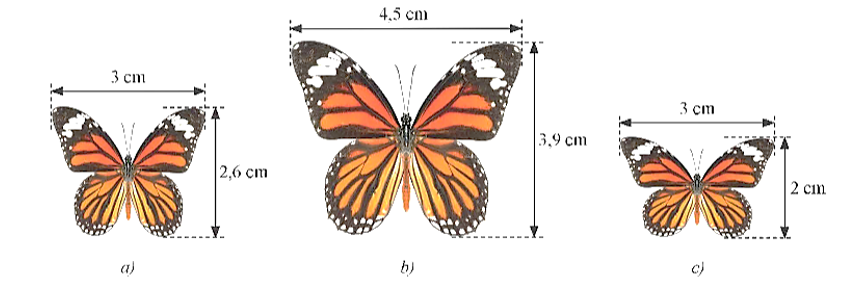
Hình a) và hình b).
Hình a) và hình c).
Hình b) và hình c).
Cả ba hình.
Năm nay tuổi bố gấp \(10\) lần tuổi Minh. Bố Minh tính rằng sau 24 năm nữa thì tuổi bố chỉ gấp \(2\) lần tuổi Minh. Gọi tuổi của Minh hiện nay là \(x\) \(\left( {x \in \mathbb{N}} \right)\).
a) Sau 24 năm nữa tuổi của Minh là \(x + 24\) (tuổi).
b) Sau 24 năm nữa tuổi của bố Minh là \(10x + 24\) (tuổi).
c) Sau 24 năm nữa thì tuổi bố chỉ gấp \(2\) lần tuổi Minh nên phương trình mô tả bài toán là:
\(10x + 24 = 2x + 24\).
d) Tuổi của bố Minh hiện tại là \(30\) tuổi.
Cho tam giác \(ABC\). Trên cạnh \(AB,AC\) lần lượt lấy các điểm \(E,D\) sao cho \(AC = 3AE\) và \(AD = \frac{1}{3}AB\). Gọi \(I\) là giao điểm của \(BD\) và \(EC\). Biết rằng .
a) \(\widehat {ADB} = \widehat {AEC}\).
b) \(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\).
c) .
d) \(ID.IB = IE.IC\).
Cho biểu thức \(A = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{4}{{1 - {x^2}}}\) (\(x \ne 1\); \(x \ne - 1\)). Rút gọn biểu thức \(A\), ta được \(A = \frac{a}{{x + 1}}\) với \(a \in \mathbb{N}\). Vậy giá trị của \(a\) là:
Cho biểu thức \(M = \frac{1}{{{x^3} - 2x}}.\left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1\) với \(x \ne 2\) và \(x \ne 0\). Tính giá trị của \(M\) biết \(\left| {4 - x} \right| = 2\).
Giải phương trình sau: \(\frac{3}{2} + \frac{4}{3}\left( {3x - \frac{1}{2}} \right) = \frac{1}{3}x + 2\).
Cho tam giác nhọn \(ABC\) có \(AB = 13{\rm{ cm}}\), \(AC = 15{\rm{ cm}}\). Kẻ \(AD \bot BC\) \(\left( {D \in BC} \right)\). Biết \(BD = 5{\rm{ cm}}\), độ dài đoạn thẳng \(BC\) là
Một xe tải và một xe con cùng khởi hành từ tỉnh A đến tỉnh B. Xe tải đi với vận tốc \(30{\rm{ km/h}}\), xe con đi với vận tốc \({\rm{45 km/h}}\). Sau khi đi được \(\frac{3}{4}\) quãng đường AB, xe con tăng vận tốc \({\rm{5 km/h}}\) trên quãng đường còn lại thì đến B sớm hơn xe tải là \(2\) giờ \(27\) phút. Tính quãng đường AB.
Cho \(\Delta ABC\) vuông tại \(A\)có \(AB = 6{\rm{ cm}}\), \(AC = 8{\rm{ cm}}\).
a) Tính độ dài cạnh \(BC\).
b) Vẽ đường cao \(AH\). Chứng minh rằng .
c) Trên cạnh \(AH\) lấy điểm \(M\) sao cho \(AM = 3,2{\rm{ cm}}\), từ điểm \(M\) kẻ đường thẳng \(d\) song song với \(BC\) lần lượt cắt \(AB,AC\) tại \(E,F\). Tính \(\frac{{{S_{AEF}}}}{{{S_{ABC}}}}\).
Với \(n \in {\mathbb{N}^*}\), tính tổng sau: \(A = \frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{\left( {2n - 1} \right)\left( {2x + 1} \right)}}\).








