Bộ 10 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án (Đề 7)
11 câu hỏi
Cho các nội dung sau:
(1) Tìm điều kiện xác định của phương trình.
(2) Xét mỗi giá trị tìm được của ẩn, giá trị nào thỏa mãn điều kiện xác định thì đó là nghiệm của phương trình đã cho.
(3) Giải phương trình vừa nhận được.
(4) Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu.
Sắp xếp các nội dung trên theo thứ tự các bước để giải phương trình chứa ẩn ở mẫu là
(1), (2), (3), (4).
(1), (3), (2), (4).
(1), (4), (2), (3).
(1), (4), (3), (2).
Phương trình nào dưới đây nhận cặp số \(\left( { - 2;\,\,4} \right)\) làm nghiệm?
\(x - 2y = 0\).
\(2x + y = 0\).
\(x - y = 2\).
\(x + 2y + 1 = 0\).
Trong tam giác \[ABC\], nếu \(\widehat B = 30^\circ \) thì tỉ số giữa cạnh đối \(AC\) và cạnh huyền \(BC\) bằng
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{1}{2}\).
\(\frac{{\sqrt 2 }}{2}.\)
1.
Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \(\alpha + \beta = 90^\circ .\) Khẳng định nào sau đây là đúng?
\(\tan \alpha = \cot \beta .\)
\(\tan \alpha = \sin \beta .\)
\(\tan \alpha = \cos \beta .\)
\(\tan \alpha = \tan \beta .\)
Cho \(a < b.\) Khi đó
a) \(4a - 2 > 4b - 2.\)
b) \(6 - 3a < 6 - 3b\).
c) \(4a + 1 < 4b + 5.\)
d) \(7 - 2a > 4 - 2b.\)
Biết đường thẳng \(y = ax + b\) đi qua hai điểm \(M\left( {3;\,\, - 5} \right)\) và \(N\left( {1;\,\,2} \right).\) Tính tổng bình phương của \(a\) và \(b.\)
Cho tam giác \[ABC\] vuông tại \[C\] có \[BC = 1,2\,\,{\rm{cm}}\,{\rm{, }}AC = 0,9\,\,{\rm{cm}}.\] Tính \[\sin B + \cos B.\]
(2,5 điểm)
1. Giải các phương trình sau:
a) \(\left( {1 - 2x} \right)\left( {x + 5} \right) = 0.\)
b) \(\frac{{2x - 5}}{{x + 4}} + \frac{x}{{4 - x}} = \frac{{17x - 56}}{{16 - {x^2}}}.\)
2. Giải các bất phương trình sau:
a) \(5 + \frac{2}{3}x > 3\).
b) \[{\left( {x - 1} \right)^2} < x\left( {x + 3} \right).\]
c) \[\frac{{2x - 1}}{3} - \frac{{x + 2}}{2} < \frac{{5x + 4}}{6}.\]
(2,0 điểm)
1. Tìm các hệ số \(x\) và \(y\) trong phản ứng hóa học đã được cân bằng sau:
\(x{\rm{KCl}}{{\rm{O}}_3} \to 2{\rm{KCl}} + y{{\rm{O}}_2}.\)
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Anh Hoài đã đến phòng tập thể dục và tập 40 phút Yoga, sau đó nhảy Jumping jacks 10 phút và tiêu hao được 510 calo. Lần tiếp theo anh Hoài tập 30 phút Yoga và thực hiện nhảy Jumping jacks 20 phút, lượng calo tiêu hao được là 470 calo. Hỏi có bao nhiêu calo đã tiêu hao trong mỗi phút tập Yoga? Có bao nhiêu calo đã tiêu hao trong mỗi phút tập Jumping jacks?
1. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\) và \(\widehat {C\,} = 32^\circ .\) Tính độ dài các cạnh còn lại của tam giác \(ABC\) (kết quả làm tròn đến hàng phần trăm).
2. Một chiếc thang \(AC\) được dựng vào một bức tường thẳng đứng (hình vẽ).
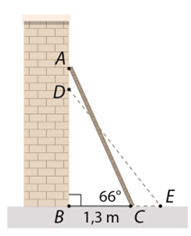
– Ban đầu khoảng cách từ chân thang đến tường là \(BC = 1,3{\rm{\;m}}\) và góc tạo bởi thang và phương nằm ngang là \(\widehat {ACB} = 66^\circ \).
– Sau đó, đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}}\) đến vị trí \(D.\) Khi đó, góc \(DEB\) tạo bởi thang và phương nằm ngang bằng bao nhiêu (Kết quả số đo góc làm tròn đến phút)?
(0,5 điểm) Cho góc \(\alpha \) thỏa mãn \[0^\circ < \alpha < 90^\circ .\] Chứng minh rằng: \[\frac{{\sin \alpha + \cos \alpha - 1}}{{1 - \cos \alpha }} = \frac{{2\cos \alpha }}{{\sin \alpha - \cos \alpha + 1}}.\]








