Bộ 10 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án (Đề 5)
17 câu hỏi
Điều kiện xác định của phương trình \(\frac{x}{{x - 3}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x - 3} \right)}}\) là
\[x \ne - 2;{\rm{ }}x \ne 3\].
\[x \ne 2;{\rm{ }}x \ne --3\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\[x \ne 0;{\rm{ }}x \ne 3\].
Nghiệm của phương trình \(9{x^2}\left( {2x - 3} \right) = 0.\) là
\[\left\{ {0;\frac{3}{2}} \right\}\].
\[\left\{ 0 \right\}\].
\[\left\{ {\frac{3}{2}} \right\}\].
\(\left\{ {0; - \frac{3}{2}} \right\}.\)
Phương trình \[4y - 3x = 5\] nhận cặp số nào sau đây làm nghiệm?
\[\left( {1\,;\,\,2} \right)\].
\[\left( {2\,;\,\,1} \right)\].
\[\left( {2\,;\,\,2} \right)\].
\(\left( {1\,;\,\,1} \right).\)
Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}x + y = 5\\2x - y = 4\end{array} \right.\]?
\[\left( { - 3\,;\,\,2} \right)\].
\[\left( {3\,;\,\,2} \right)\].
\[\left( {3\,;\,\, - 2} \right)\].
\[\left( { - 3\,;\,\, - 2} \right).\]
Bất đẳng thức nào sau đây đúng với mọi số thực \(a?\)
\(5a > 3a.\)
\(3a > 5a.\)
\(5 + a > 3 + a.\)
\ ( - 3a> - 6a. \)
Nếu \[a < b\] thì 2a+1....2b+1.Dấu thích hợp điền vào ô trống là
\[ \ge \].
\[ \le \].
\[ < \].
</>
\[ > \].
Bất phương trình \[4x + 1 < 2x - 9\] có nghiệm là
</>
\[x \ge - 5.\]
\[x < - 5\].
\[x \le - 5\].
\[x \le - 5\].
Giá trị nào dưới đây thỏa mãn bất phương trình \(\frac{{2x - 3}}{3} \le \frac{{3x - 2}}{4}\)?
\(x = - 7.\)
\(x = - 6.\)
\(x = - 8.\)
\(x = - 9.\)
Cho \(\alpha = 40^\circ \) và \(\beta = 50^\circ .\) Khẳng định nào sau đây là đúng?
\(\sin \alpha = \sin \beta \).
\(\cos \alpha = \cos \beta \).
\(\tan \alpha = \cot \beta \).
\(\tan \alpha = \tan \beta \).
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha .\) Tỉ số \(\frac{{HA}}{{HC}}\) bằng:
\(\sin \alpha \).
\[\cos \alpha \].
\(\tan \alpha \).
\(\cot \alpha \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 10\,\,{\rm{cm}},\,\,\widehat C = 40^\circ .\) Cạnh \(BC\) có độ dài gần nhất với kết quả nào dưới đây?
\(12,45\)cm.
\(15,56\,\,{\rm{cm}}{\rm{.}}\)
\(6,43\,\,{\rm{cm}}{\rm{.}}\)
\(8\)cm.
Cho tam giác\(ABC\)vuông tại\(A\)có \(AB = 8\,\,{\rm{cm}},\,\,\widehat C = 30^\circ .\) Độ dài cạnh \(BC\) là
4 cm.
\(8\sqrt 3 \,\,{\rm{cm}}\).
\(\frac{{8\sqrt 3 }}{3}\,\,{\rm{cm}}\).
16 cm.
(1,0 điểm) Giải các hệ phương trình sau:
a) \[\left\{ \begin{array}{l}2x + y = 4\\5x - y = 10\end{array} \right.\].
b) \[\left\{ \begin{array}{l}4x - 3y = 6\\0,4x + 0,2y = 0,8.\end{array} \right.\]
(2,5 điểm)
1. Giải các phương trình sau:
a) \[2x\left( {3x - 1} \right) = \left( {3x - 1} \right)\];
b) \(\frac{{x + 3}}{{x - 3}} = \frac{3}{{{x^2} - 3x}} + \frac{1}{x};\)
2. Giải các bất phương trình sau:
a) \(3\left( {x - 2} \right) - 5 \ge 3\left( {2x - 1} \right);\)
b)\[3 < \frac{{2x - 2}}{8}\]
c) \(\frac{{x - 1}}{2} - \frac{{7x + 3}}{{15}} \le \frac{{2x + 1}}{3} + \frac{{3 - 2x}}{5}.\)
(1 điểm) Một khu vườn hình chữ nhật có chu vi bằng \[68{\rm{ m}}.\] Nếu tăng chiều rộng lên gấp đôi và chiều dài lên gấp ba thì chu vi khu vườn mới là \[178{\rm{ m}}.\] Tính diện tích ban đầu của khu vườn.
(2,0 điểm)
1. Cho tam giác \[ABC\] vuông tại \[A\,\,\left( {AB < AC} \right)\], đường cao \(AH.\) Biết \(AB = 6\,\,{\rm{cm}}\) và \(\cos \widehat {ABC} = \frac{3}{5}\). Tính \(BC,\,\,AC,\,\,BH.\)
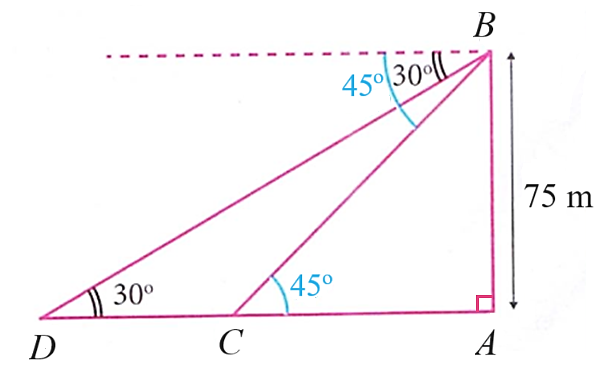
2. Từ trên một ngọn hải đăng cao \(75\,\,{\rm{m}}\), người ta quan sát hai lần thấy một chiếc thuyền đang hướng về phía hải đăng với góc hạ lần lượt là \(30^\circ \) và \(45^\circ \) (xem hình vẽ). Hỏi chiếc thuyền đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn kết quả đến hàng đơn vị)

(0,5 điểm) Giải bất phương trình sau: \(\frac{{x - 2}}{{2017}} + \frac{{x - 3}}{{2018}} < \frac{{x - 4}}{{2019}} + \frac{{x - 5}}{{2020}}.\)
</>








